考虑运输—生产—库存集成的精益供应链模型

缪 周，徐克林，朱 伟

MIAO Zhou,XU Ke-lin,ZHU Wei

（同济大学 机械工程学院，上海 201804）

0 引言

20世纪90年代以来，供应链管理已经成为现代企业的重要管理模式。其中供应链的模型与优化成为供应链研究和应用发展的重要方向[1-5]。将精益技术从生产管理扩展到供应链层面，从整体上对供应、制造、存储、分销、物流等环节加以分析和优化，使整个供应链实现精益化[6]。精益供应链正是源于精益生产，它将从产品设计直至顾客得到产品的整个过程所必需的步骤和合作伙伴整合起来，快速响应顾客多变的需求，减少各种浪费，用尽可能少的资源最大程度地满足客户需求[7]。当前企业竞争优势已不再来源于制造的产品而是整合企业内外部资源的能力。1988年Cohen和Lee[8]首次提出了产销集成系统的模型框架。Pyke和Cohen[9,10]开发了单一产品及多产品的三个层次的Markov链模型。Chandra和Fisher[11]将生产批量与车辆路径问题整合起来进行研究。Chien[12]研究了多工厂、单产品的网络中的最大化生产和运输数量的问题。Kim和Ha[13]建立了供应链环境下采购商-供应商集成总成本库存决策模型。Hill[14]讨论了集成库存模型中对订单采用多次交付方式的优点，证明了JIT环境下联合分批策略能显著降低总成本。聂兰顺等[15]以供应商和采购商组成的供应链为研究对象，建立了考虑运输成本的JIT采购批量分割决策模型。

但这些模型没有考虑运输合并，也未能将供应链的产、供、销等有效集成起来，无法真正实现供应链精益化。本文综合考虑运输、生产、库存等环节，并且将采购与分销运输进行合并，建立精益供应链模型，通过求解模型，确定最优的决策变量，实现供应链成本最低的目标。

1 模型的构建

1.1 模型的假设

1）N个供应商、1个核心企业、K个客户构成一产品供应链。核心企业至供应商和客户采用多频次循环取货（milk-run）方式，且将采购与分销进行合并运输，一次采购与分销批量即为一次运输批量；

2）以运输次数和里程计算运输成本，即运输成本包括运输启动成本与里程成本之和；

3）客户、核心企业和供应商处各持有一定量的安全库存，数量预先已经设置；

4）供应商、核心企业均采用双看板拉动的JIT生产和JIT送货；

5）核心企业、供应商和客户的生产率/需求率是确定的。

1.2 模型的符号及说明

1.2.1 已知常量

T：核心企业的一个生产周期，单位为月；

V：为运输车辆的平均速率，单位为公里/小时；

Pm、Ps、Dc分别为核心企业、供应商和客户在周期 内的生产率/需求率，单位为件/周期；

USCs、USCm分别为供应商、核心企业每批次生产的启动成本，单位为元/次；

UPCs、UPCm分别为供应商、核心企业的单位生产成本，单位为元/件；

FOC、FOC'分别为零部件、成品的订货固定成本，单位为元/次；

FDC为零部件和成品的运输启动成本，单位为元/次；

UDC为零部件和成品的单位运输成本，单位为元/件；

UICs、UICm、UICd为供应商、核心企业及在途零部件单位库存成本，单位为元/件；

UIC'm、UIC'c、UIC'd分别为核心企业、客户及在途的成品单位库存成本，单位为元/件；

SIs、SIm分别为供应商、核心企业持有的零部件的安全库存量，单位为件；

SI'm、SI'c分别为核心企业、客户持有的成品的安全库存量，单位为件。

1.2.2 待决策变量及变量的函数

q：每次运输批量，单位为件/次；

n：周期 内的运输频次，单位为次；

dr：一次循环取货的距离，单位为公里；

tc：周期 内产品的供应链总成本，单位为元；

tpc、tdc、tic分别为周期T内生产、运输、库存总成本，单位为元；

ais、aim、aid分别为周期T内供应商、核心企业及在途的零部件平均库存量，单位为件；

ai'm、ai'c、ai'd分别为周期T内核心企业、客户及在途的成品平均库存量，单位为件。

1.3 模型的建立

1.3.1 目标函数

优化目标是供应链总成本最低，即

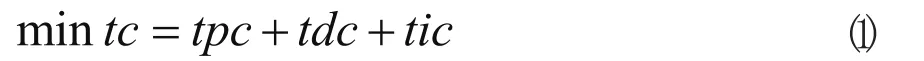
其中，tpc为零部件和成品的制造成本与生产启动成本之和，即

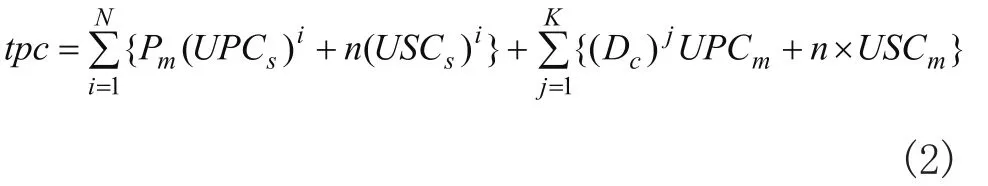
tdc为零部件和成品的订货成本与运输成本之和，即

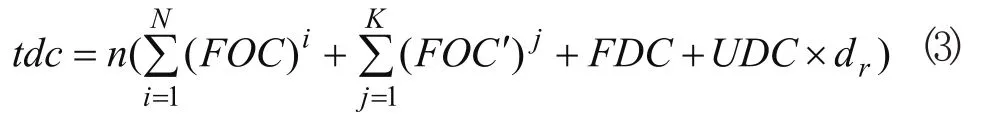
tic为供应商、核心企业及在途零部件库存成本与核心企业、客户及在途成品库存成本之和，即

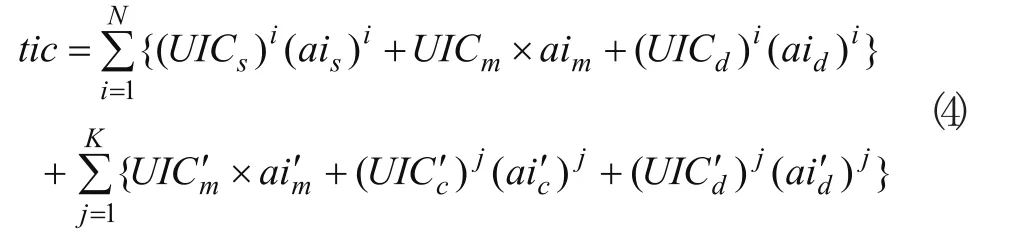
周期T内，模型的库存变化规律如图1所示。故供应商、核心企业及在途零部件平均库存量分别为式(5)、(6)和(7)。

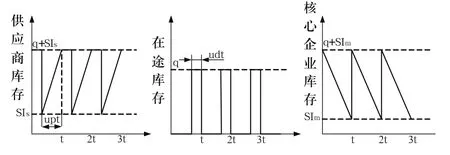
图1 模型的库存变化规律

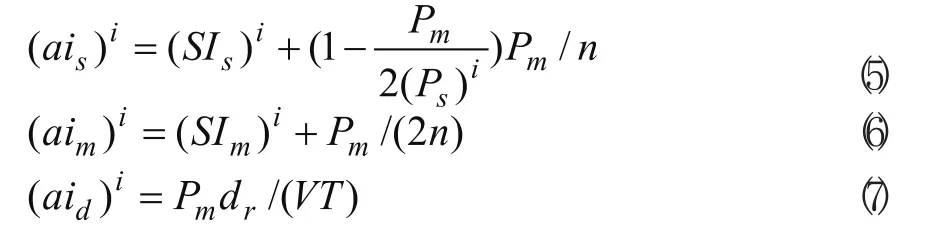
同理，核心企业、客户及在途的成品平均库存量分别为式(8)、(9)和(10)。

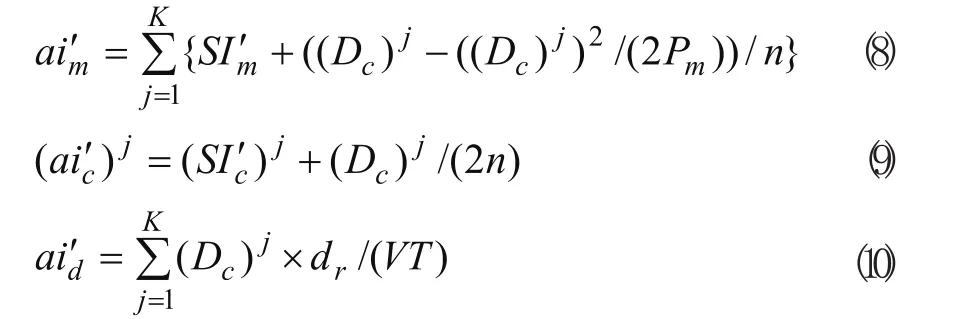
将式(2)-(10)一并代入式(1)，得

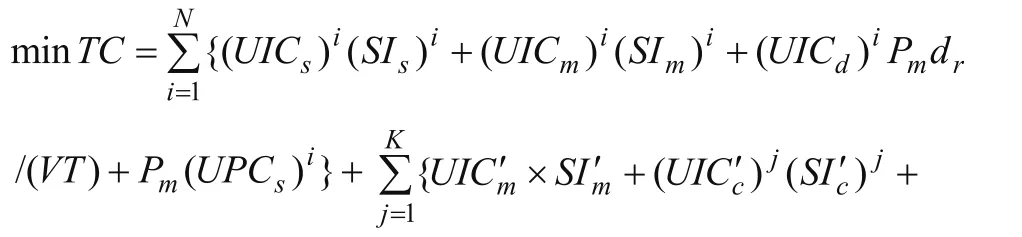
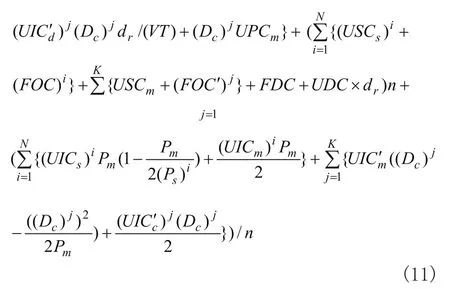
图2 算法流程

1.3.2 约束条件

1）每个供应商或客户只容许访问一次。

2）每个供应商或客户只被包含在一条循环取货路径中。

3）每条循环取货路径上的供应商或客户具有相同的取货频率。

4）一个生产周期内的运输频次必须为整数，否则无法操作。即n∈int，且n≥0。

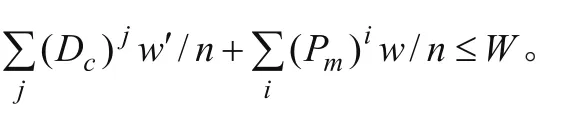
1.4 模型的求解

首先采用改进蚁群算法求出最优运输路径的长度dr，再将目标函数式(11)看成变量为n的凸函数，当且仅当d(tc)/d(n)=0时，n*使得tc取得最小值。

针对基本蚁群算法易于出现早熟、停滞现象，本文采用2-opt局部搜索策略以及信息素在线延迟更新方式等方法对其进行改进。算法流程如图2所示。

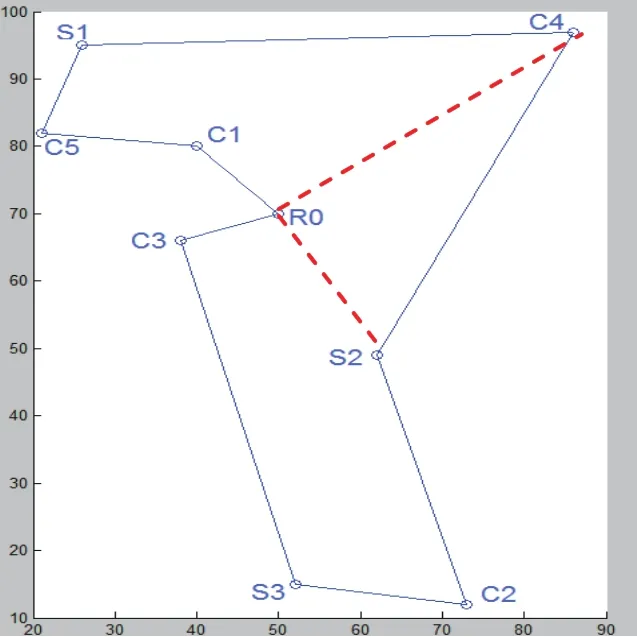
图3 仿真结果

2 案例分析

R企业是一家汽车零部件制造商，其中车轮饰盖产品供应链共有3家供应商、5家客户。为实施精益供应链运作模式，要求各供应商JIT供货，同时R企业也向客户JIT送货。采用采购和分销合并运输的方式来降低运输成本。以供应链总成本最低为优化目标，R企业需作出如下决策：选择最优运输路径、最优运输频次以及最优运输批量。

2.1 供应链具体数据

以1个月（30天）为生产周期，各企业的地理位置见表1，每单位直线距离相当于实际1公里。采用最大载重20吨的货车完成循环取货的运输任务，一次发车的固定成本为1000元，每公里运输成本为5元，运输速率为50公里/小时，不计装卸时间。其他数据如表2所示。

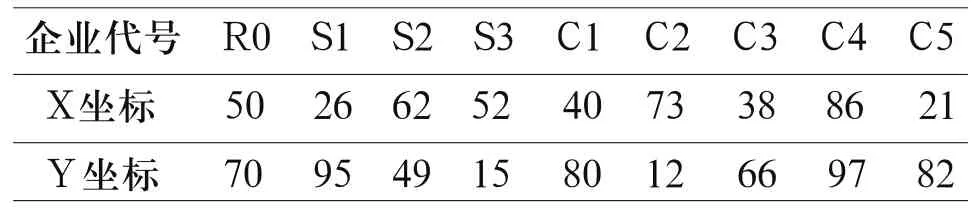
表1 各企业的地理坐标

2.2 决策变量的求解

采用改进蚁群算法求出采购与分销合并运输的最优路径。在matlab R2009a仿真环境下，参数选取如下：m=9，α=1，β=5，ρ=0.1，ε=0.1，M=0.0004，Q=100，NC=200，仿真结果如图3所示。即最优运输路径为：R0-C1-C5-S1-C4-S2-C2-S3-C3-R0，路径长度约为286km。

根据上述求解过程，结合具体数据，求出最优运输频次。即n*≈18.8。

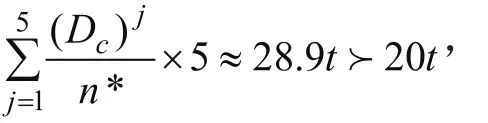
2.3 最优决策

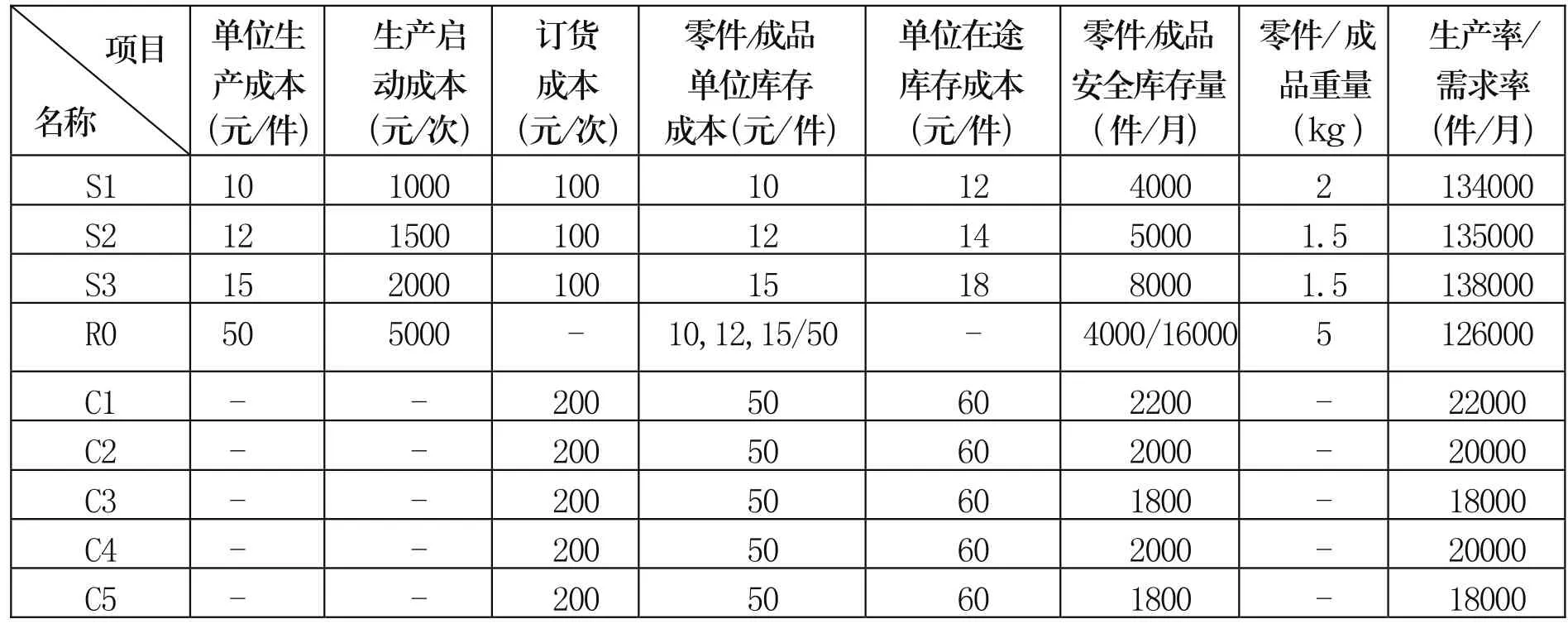
表2 供应链上各企业具体数据

根据上述求解过程，可知最优决策如下。

运输路径1：R0-C1-C5-S1-C4-R0，频次：19，批量：15.8t-5.8t-4.7t+13.3t-5.3t；

运输路径2：R0-C3-S3-C2-S2-R0，频次：19，批量：10t-4.7t+9.9t-5.3t+9.9t。

此时，路径1最大装载率达93%，路径2最大装载率达99%，供应链总成本实现最小化，为15,766,546元。

3 结束语

运输成本在产品物流成本中的高比重和运输费率的复杂性决定了考虑运输成本的物流决策是复杂而又具有实际意义的问题。本文针对多供应商、单一核心企业及多客户构成的产品供应链，建立了集成运输、生产、库存成本的精益供应链模型，解决了以供应链总成本最低为优化目标的采购与分销决策问题和运输决策问题。经案例和仿真实验验证，模型及求解方法简单，实用性强。进一步的研究可以考虑多产品、随机性生产率和需求率的情况。

[1] Mabert V A,Vankataramanan M A.Special research focus on supply chain linkages：challenges for design and management in the 21st century[J].Decision Science,1998,29(3)：537-552.

[2] Erengue S S,Simpson N C,Vakharia A J.Integrated production distribution planning in supply Chain：an invited review[J].European Journal of Operation Reseach,1999,115(2)：219-236.

[3] Malori M,Benton W C.Supply chain partenerships：opportunities for operation research[J].European Journal of Operation Reseach,1997,101(3)：419-429.

[4] Sharafali M,Co HC.Some models for understanding the cooperation between the supplier and the buyer[J].International Journal of Production Research,2000,38(15)：3425-3449.

[5] Sabri E H,Beamon B M.A multi-objective approach to simultaneous strategic and operational planning in supply chain design[J].International Journal of Management Science,2000,28(6)：581-598.

[6] Phelps T,Smith M,Hoenes T.Building a lean supply chain[J].Manufacturing Engineering,2004,132(5)：107-111.

[7] Vitasek K,Manrodt K B,Abbott J.What makes a lean supply chain?[J].Supply Chain Management Review,2005 (9)：39-45.

[8] Cohen M A,Lee H L.Strategic analysis of integrated production distribution systems：models and methods[J].Operations Research,1988,36(2)：216-228.

[9] Pyke D F,Cohen M A. Performance characteristics of stochastic integrated production distribution systems[J].European Journal of Operations Research,1993,68(1)：23-48.

[10]Pyke D F,Cohen M A. Multiproduct integrated production distribution systems[J].European Journal of Operations Research,1994,74(1)：18-49.

[11]Chandra P,Fisher M L.Coordination of production and distribution planning[J].European Journal of Operations Research,1994,72(3)：503-517.

[12]Chien T W.Determining profit maximizing production/shipping policies in a one-to-one direct shipping stochastic environment[J].European Journal of Operational Research,1993,64(2)：83-100.

[13]Kim S L,Ha D.A JIT Lot-splitting Model for Supply Chain Management：Enhancing Buyer-supplier Linkage[J].International Journal of Production Economics,2003,86(1)：1-10.

[14]Hill R M.The Single-vendor Single-buyer Integrated Production Inventory Model with a Generalized Policy[J].European Journal of Operational Research,1997,97(3)：493-499.

[15]聂兰顺,徐晓飞,战德臣.考虑运输成本的JIT采购模型及算法[J].中国机械工程,2007,18(23)：2835-2839.