三维钝体结构风压分布与绕流特性的大涡模拟研究

汪大洋，周 云，谭 平

(1.广州大学土木工程学院，广东 广州 510006;2.广州大学工程抗震研究中心，广东 广州 510405)

0 引言

钝体绕流与风压分布特性研究是结构风工程中非常重要的内容，是认识结构周围风环境、掌握结构表面风压分布的主要途径之一，对结构抗风设计具有重要的参考、指导价值。近年来，国内外研究人员在模拟预测全尺寸或缩尺比例结构模型的绕流状态、风压分布、相互干扰效应等方面进行了较多的研究工作。Selvan［1］等采用LES(Large Eddy Simulation)模型对一足尺风洞实验进行了研究，结果表明对平均值的预测与实测结果吻合较好，但对峰值压力，只有根据实测数据生成脉动来流条件的模拟结果与实测吻合较好。Tutar［2］等人采用了大涡模拟法对两栋平行建筑物进行了数值研究，给出了平行布置的建筑物的风荷载和流场的分布特点。Muralami［3］、Yu Da-hai［4］应用 LES 模型对钝体绕流进行的研究表明，LES模型虽能准确反映绕流的复杂特征，但因计算量大而难以在工程中应用。Cheng［5］等采用LES和RANS(Reynolds-Averaged Navier-Stokes)对比研究了群体结构绕流特性，结果表明二者均能很好预测群体结构平均气流的主要特性，但LES预测结果与试验的吻合性优于 RANS。Shah和 Ferziger［6-7］通过研究得出LES模型能为风工程研究人员提供风压分布特性、绕流状态等重要信息。Hee［8］等采用LES研究了一位于湍流边界层的矩形建筑，结果表明合理的来流及计算域边界可大大提高LES与试验结果的吻合性。李正良［9］等针对复杂高层进行了风洞和数值研究，表明RSM模型能较好地模拟结构周围的流场，试验与数值结果吻合性较好。王小华［10］等对方形钝体受限绕流进行了模拟，结果表明均匀来流下湍流场沿槽道轴面对称，LES能捕捉到丰富的涡系及涡动时变过程。吴文权［11］、陈斌［12］等采用离散涡法对多个钝体绕流的研究表明，即使来流是稳定的，绕多个钝体流动也会出现不稳定的流动。

虽然已有学者对钝体结构的绕流问题进行了相关研究，但由于钝体绕流的复杂性，流场与结构之间的很多问题还没有清晰解决，且已有研究大多针对均匀来流进行的，较少考虑来流脉动特性，而实际工程显然处于湍流脉动风场中，存在复杂的湍流脉动现象。因此，有必要对绕流问题进一步开展研究。本文针对三维矩形钝体结构，以平均风速和脉动风速作为入口边界条件，采用大涡模型研究该钝体的分压分布与绕流特性，再现钝体绕流的冲撞、分离、重附着及尾流漩涡不对称脱落现象，揭示钝体绕流分离、重附着、漩涡生成、发展等的形成机理，并阐述钝体绕流对其来流方向、上部及尾流速度场及表面风压场分布的影响规律。

1 控制方程与离散方法

1.1 LES控制方程

大涡模拟的基本方法是对大尺度涡旋进行直接模拟，对小尺度涡旋作模式假定，因此大涡模拟必须引入滤波函数来修改Navier-Stokes方程(N-S方程)，使得高波数的波被截断，但能量传递过程仍保留。经滤波函数滤波后，LES控制方程为:

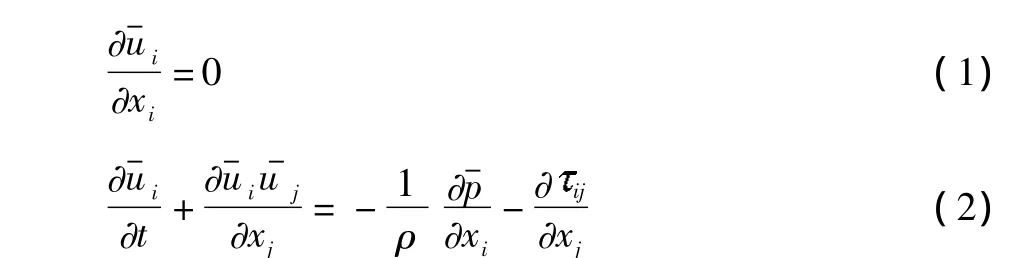
Smagorinsky认为，对于局部各向同性湍流，如果假定湍流的产生项和耗散项达到平衡，则亚网格尺度应力可定义为:

式(3)即为代数压网格尺度模型，又称Smagorinsky模型［13］，式中应变率张量为:

1.2 数值离散与求解

采用有限体积法离散过滤后的不稳定N-S方程，采用时间积分算法进行时间积分，进而从速度项中分离压力项。采用二阶精确中心差分逼近法来离散空间LES控制方程，以 QUICK(Quadratic Upstream Interpo-lation Convective Kinematics)方式采用二阶上游有限差分法离散空间对流项［14，15］。若 n△t时刻变量已知，则(n+1)△t时刻变量的计算如下:

1)将二阶后差欧拉法与显示二阶Adams Bashforth算法相结合，考虑已知压力场，采用二阶时间法计算中心速度项U*:

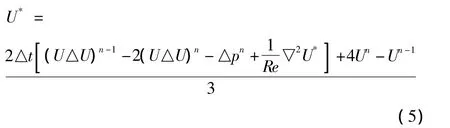
2)采用Helmholtz分解定理将中心速度场投射到离散自由向量场的子空间上:

令:φ =pn+1-pn。

3)利用超松弛迭代法通过求解泊松方程计算压力场，并得到增量压力:

4)计算(n+1)△t时刻的变量:

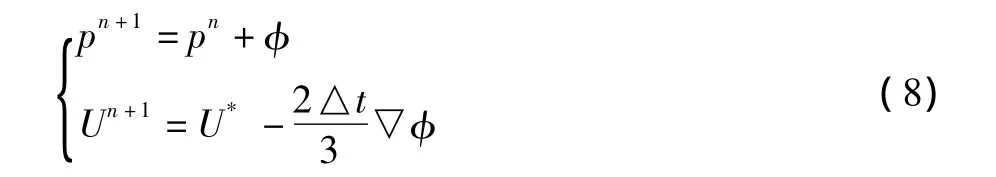
2 计算模型与边界条件

2.1 计算模型

基于ADINA软件建立计算模型，采用三维流体单元模拟流场，空气流体质量密度取1.29kg/m3，粘度取1.79×10-5kg/(m·s)，采用FCBI-C单元对流体域进行离散［16］。钝体缩尺比例为1∶200，风速相似系数取1/5，参考高度风速vref=5.66m/s。计算域的选取应足够大，以使边界条件对绕流的影响降至最低［17-18］，本文取l(x)×l(y)×H=0.6m×0.4m×1.0m，计算域为24H×18H×10H，其中钝体前方 L1(x)=7H、后方 L2(x)=16H。分析工况及单元划分情况见表1。图1为工况1流体域与钝体尺寸布置图。先对计算域进行稳态分析，然后进行瞬态分析，瞬态分析的时间步长为0.001s，总时间为3.6s。

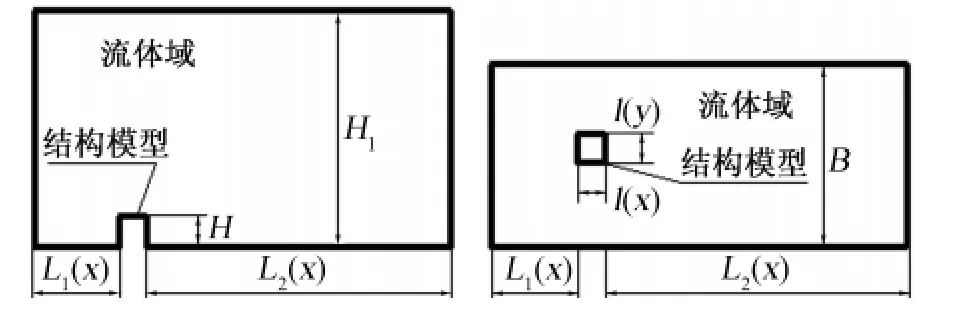
图1 流体域与结构模型示意图Fig.1 Sketch of fluid field and bluff body

2.2 边界条件

为提高数值模拟的精确性，在数值风洞入口边界条件上同时施加平均风速和脉动风速。平均风速剖面采用指数律:

式中:zref、vref为参考高度和相应的平均风速;z、v(z)为任意高度和相应的平均风速;α为地面粗糙度指数，取α=0.22。

脉动风速采用 AR法(Auto-Regressive)生成［19-21］，模型阶数为5阶，时间步长为0.001s，脉动风速谱为Davenport谱。脉动风速的计算公式如下(模拟功率谱与目标功率谱的对比如图2所示):

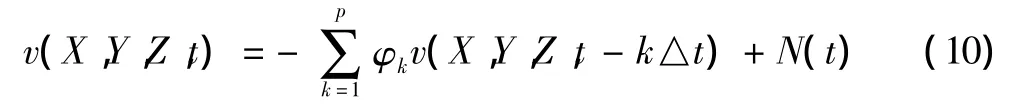
式中:X={x1，x2，…，xm}，Y={y1，y2，…，ym}，Z={z1，z2，…，zm}，(xi，yi，zi)为空间第 i点坐标，(i=1.2，…，m);△t为时间步长;p为模型阶数;φk为AR模型的自回归系数矩阵，为m×m阶矩阵，(k=1.2，…，p);N(t)为独立随机过程向量。

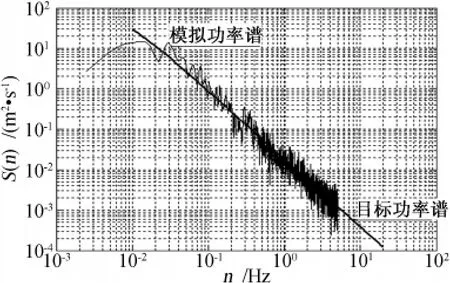
图2 功率谱函数对比Fig.2 Contrast of power spectrums

入口湍流强度采用日本规范建议［22］:

表2给出了计算域与钝体的参数设置。

表1 分析工况Table1 Analysis cases

表2 计算模型参数设置Table2 Calculation parameters

3 数值分析验证

为验证上述数值计算方法、边界条件选取等的可行性及计算结果的可信度，首先进行一正方体钝体的绕流特性分析，并将分析结果与已有研究对比［23-25］。该正方形钝体所处流场尺寸为15L×5L×10L(L为钝体特征尺寸)，模型X、Y、Z三个方向单元网格数量依次为48、43和38(如图3所示)。

图4显示了流场横风向风速剖面与已有研究的对比，图5显示了钝体表面压力系数分布与已有研究的对比。由图4、图5可知，虽然由于模型边界条件、湍流度、阻塞效应等原因引起本文研究结果与已有试验和数值研究结果局部存在一定的差异(如钝体顶面、侧面风压分布)，但总体流场特征和风压系数分布与已有研究仍具有较好的吻合性，说明通过本文方法进行流场数值模拟是可信的，进而为下文分析提供可靠保证。

同时，针对工况1采用不同湍流模型进行对比研究。图6显示了模型中剖面速度分布图。可见，三种湍流模型风速剖面的吻合性很好，进一步证实了本文方法的可行性。

4 结果分析与讨论

4.1 绕流特性

图7显示了工况1的切平面A的竖向风速剖面随时间的分布。图8显示了工况1的竖向风速剖面图。图9显示工况5的竖向风速剖面图。由图7、图8和图9可知:

①来流区风速剖面随时间变化较小，在x/H＜-0.25范围内，风速剖面因受钝体影响较小而随时间基本不变，但在-0.25＜x/H＜0内，风速剖面受钝体阻碍作用随时间有一定的变化，但变化幅度不大;屋顶区和尾流区风速剖面在初始时刻随时间变化较大，但随时间增长而逐渐减小，1.5s后基本无变化，说明流场已发展到稳定状态;

②来流区z/H＜-0.25内，因钝体对该区域流场影响较小，风速剖面沿高度基本按照指数律变化。在-0.25＜x/H＜0内，钝体对竖向风速剖面的影响分为四个阶段:在0＜z/H＜0.3内，受地面粗糙度及回流涡旋的影响，风速上升较快;在0.3＜z/H＜0.9内，因钝体绕流缓冲的影响风速增长缓慢;在0.9＜z/H＜1.4内，因流场在z/H=1处分离，风速因阻碍作用瞬间减小而急剧上升;在z/H＞1.4时，因钝体对流场的影响较小并逐渐减弱，风速剖面将重新按指数律变化;

③因屋顶区x/H=0处尚未形成涡旋状态，使得该处风速剖面与其它位置截然不同。在0＜x/H＜0.6(工况1)、0＜x/H＜0.4(工况5)内，屋顶绕流涡旋已经生成，风速剖面沿高度方向先负向增长后正向上升，在屋顶形成负风压区。屋顶钝体对风速剖面的影响主要集中在1＜z/H＜1.4区域，并在该区域发生绕流分离、重附着、漩涡生成、分离等复杂现象;

④尾流区风速剖面变化比较复杂，受尾流涡旋的影响，在0.6＜x/H＜2.6(工况1)、0.4＜x/H＜2.4(工况5)范围内呈“S”型变化。在x/H＞2.6(工况1)、x/H＞2.4(工况5)内，风速剖面随钝体对流场影响的逐渐减弱而向指数律转变。钝体对尾流竖向风场的影响集中在0＜z/H＜1.4内，并随与钝体之间距离的增大而逐渐减小。如在x/H=4.6处(工况1)，其影响范围0＜z/H ＜1.05。

⑤钝体对切平面A流场的影响要大于切平面C，如工况5的来流区在x/H=-0.125处，切平面C的风速剖面沿高度方向的变化趋势比切平面A、B平缓;同样在尾流区x/H=4.6处，切平面C的风速剖面由于受尾流影响较小而更加趋于指数律，切平面B次之，切平面A最差，原因在于钝体对中心区域流场的阻碍作用大于两侧流场。

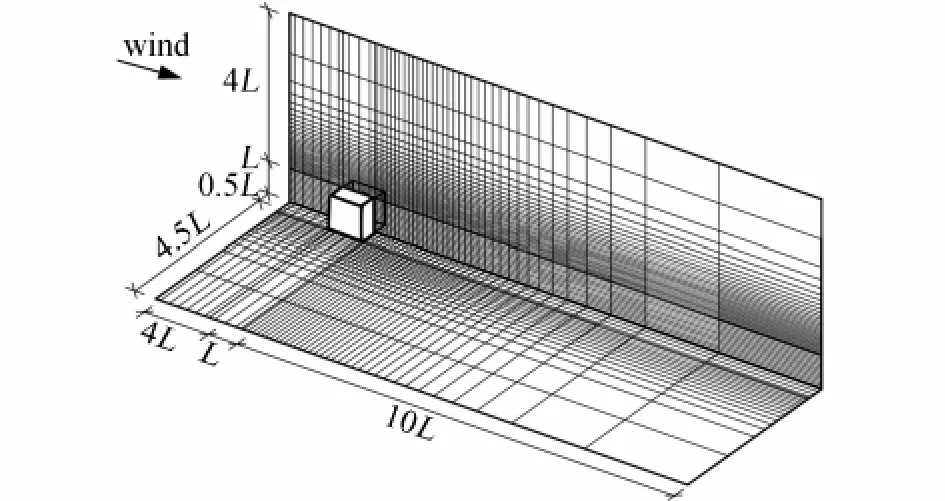
图3 计算模型Fig.3 Computational domain and grid system

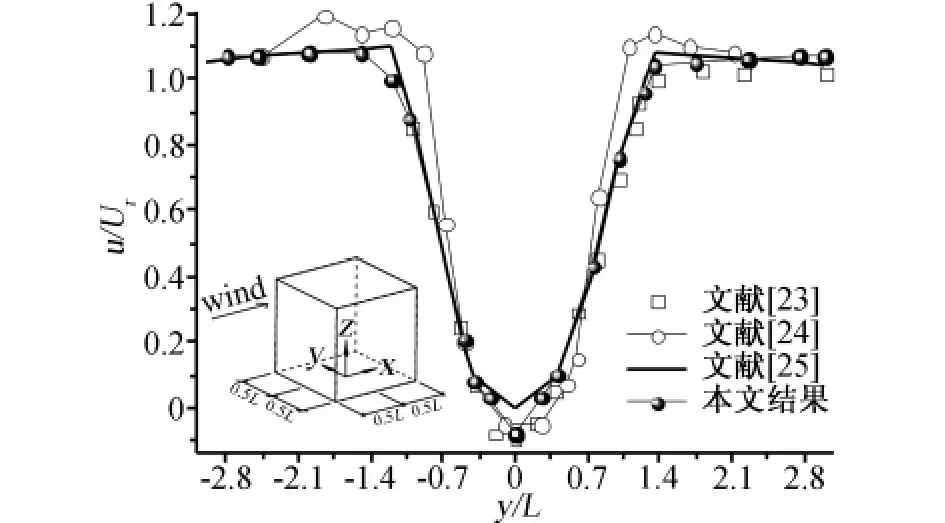
图4 横向风速剖面对比(x=2L，z=0.5L)Fig.4 Lateral velocity profile(x=2L，z=0.5L)

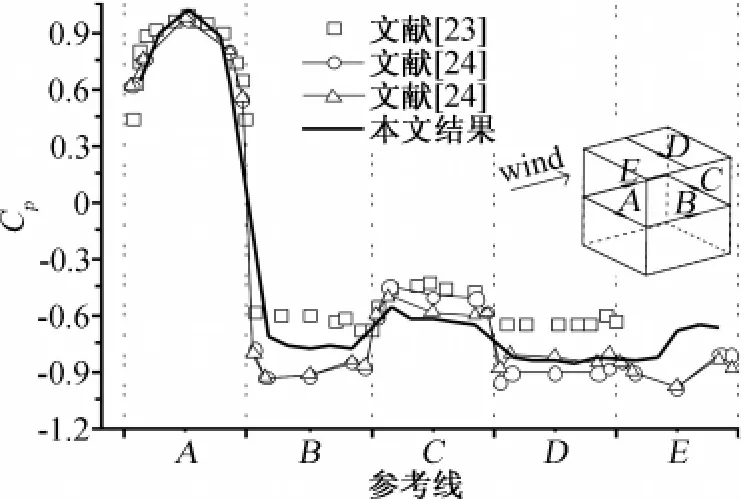
图5 钝体表面压力系数分布对比Fig.5 Surface pressure coefficients

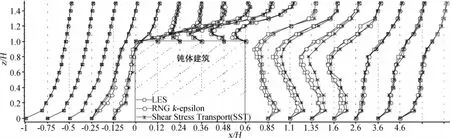
图6 风速剖面分布对比图Fig.6 Comparison of wind velocity profiles in different turbulence models

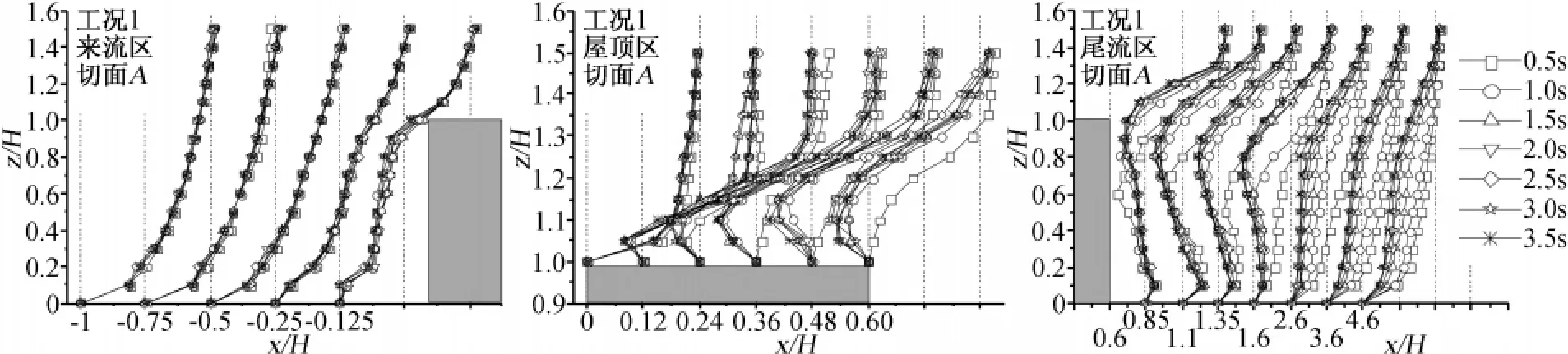
图7 竖向风速剖面随时间变化图Fig.7 Vertical velocity profiles with time

图8 工况1的竖向风速剖面图Fig.8 Vertical velocity profiles of the case 1

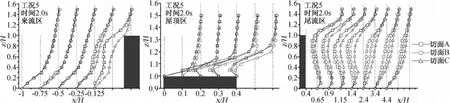
图9 工况5的竖向风速剖面图Fig.9 Vertical velocity profiles of the case 5

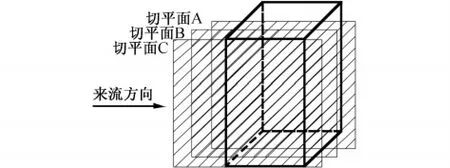
图10 切平面示意图Fig.10 Sketch map of cross section

图11显示了工况1和工况2的钝体绕流迹线示意图。表3给出了工况1的钝体绕流随时间变化的特征值。表4给出了不同工况的钝体绕流特征值(表中“∞”表示涡旋尚未形成)。为更好地揭示钝体绕流冲撞、分离、重附着及尾流涡旋的生成、发展情况，定义:将流场经过钝体拐角处发生分离的点称为分离点，将流场形成涡旋后再次与钝体或地面接触的点称为重附着点，将流场与钝体接触后而向上、下或左、右反向流动的点称为变向点，将流场跨越钝体后而在尾流区重新汇合的点称为交汇点，将流场经过钝体时直接产生的涡旋区称为主涡循环区，将由于主涡循环区对流场再次扰动而形成的涡旋区称为次涡循环区。由图11及表3、表4可知:

图11 钝体绕流迹线示意图Fig.11 Flow trace sketch

①来流区钝体绕流特性比较稳定，随时间基本无变化。如切平面A在不同时刻Z2/H均为0.8(工况1)，切平面D在不同时刻均为0.3(工况5)。

②不同切平面来流区的变向点特征值由中心向两侧减小，其原因在于流场流经钝体时，钝体对流场的阻碍作用由中心向两侧降低。如3.0s时刻切平面A、B和C的特征值Z2/H依次为0.8、0.75、0.7(工况1)。

③不同工况下尾流区均形成明显的非对称漩涡脱落现象，这与高层结构横风向振动往往大于顺风向振动的现象是一致的。其原因在于尾流涡旋的非对称脱落使结构左右两侧流场形成非对称流动，并产生不平衡的作用力，从而使结构产生横风向振动，当这种不平衡作用力上升到一定程度时，便会产生横风向振动，甚至共振现象的发生。

④图11清晰再现了钝体绕流的分离、冲撞、重附着及涡旋形成等现象，以图11(b)为例加以说明。流场经过钝体形成主涡循环区IV、V，并产生流线K和J。流线K向左上方a点运动，受钝体的影响在变向点c处分流，分别向b、d流动。在a-d区段内由于流线K与钝体发生冲撞、分离现象，而使得部分流场背离钝体向e流动，并在流线K、J之间形成次涡循环区III;另一部分在流线J和涡旋V的影响下向g运动，但由于f点为分离点，且流线K在d点处仍具有一定的速度，所以使得流线K不会平行钝体运动，而是产生弧线流d-g-h，并形成重附着点i和次涡循环区I。由于流线K与钝体在i点产生冲撞重附着，此时如果流线K的速度较小，其流动方向将会平行钝体流动;如果流线K仍具有一定速度，则会导致流线K的流动方向仍然不会平行钝体表面，而是再次产生弧线流j-k-l，并形成次涡循环区II。

⑤交汇点绕流特征值Xn/H随风向角的变化而变化，工况3和工况7的特征值最小(如两种工况下切平面G的特征值分别为1.45和1.42)，而工况5的特征值最大(Xn/H=2.25)。说明对于矩形钝体而言，来流方向与其成45°或135°角时，钝体对尾流的影响最小，并随来流方向逐渐垂直于钝体，其对尾流的影响也逐渐增大，如工况 7、8、9 的特征值依次为 1.42、1.7、2.05(G平面)。钝体对尾流影响区域均随高度的增大而减小，如工况6的切平面G、F、E、D的特征值Xn/H依次为1.85、1.7、1.6、1.2。

4.2 空间风压分布特性

为探讨不同工况下钝体绕流的空间风压分布特性，引入平均压力分布系数:

式中:pi为第i点相对压力，qref为参考风压。

图12位钝体压力参考线示意图。图13为工况1在不同时刻各参考线压力系数的分布情况，图14为不同工况下各参考线的平均压力系数分布情况。由图13、图14可知:

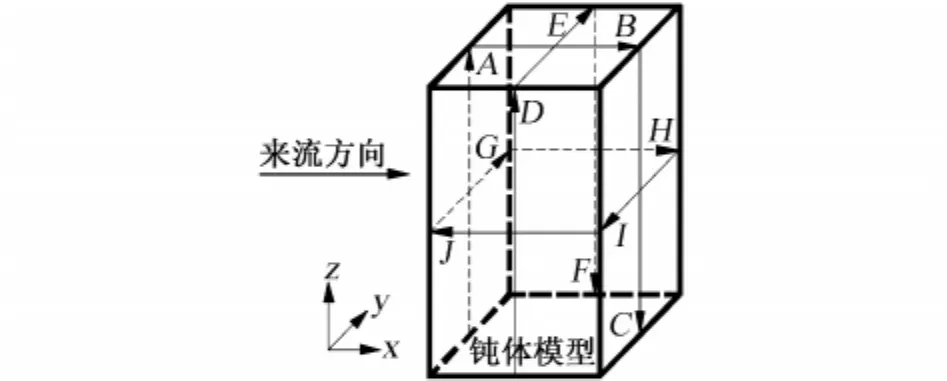
图12 参考线选取Fig.12 Selection of reference lines

①在1.5s时刻之前，各参考线的压力系数波动较大，流场未达到稳定状态;1.5s之后流场逐渐进入稳定状态，各参考线上压力系数分布渐趋稳定，波动幅度明显减小。

②迎风面压力系数分布比较均匀(如工况1、工况5、工况9)，沿高度方向均呈现由大变小再逐渐增大并在顶部再次回落的趋势，最大值出现在变向点附近。其余工况迎风面压力系数亦有类似结论，但压力系数相对较小。

③屋顶区压力系数在各工况下均为负值(参考线B、E)，平均风压为吸力。当风场垂直钝体时，屋顶区风场在迎风面前缘分离，分离处风速动能增加，使得屋顶上部一定范围内的风场趋于较低的分离流线，并沿分离流线方向形成柱状涡旋，进而造成了屋顶区沿分离流线方向的压力系数基本相等，如工况1、工况9参考线E上的压力系数;而当风场与钝体存在一定夹角时，迎风面前缘分离流线变为两条，沿每条分离流线方向的流场分离速度逐渐增大，进而沿着分离流线方向形成锥形涡，这就使得平行分离流线方向的其它参考线上的压力系数不相等，如工况7的参考线B、E的压力系数。

④随着风向角的增加，钝体迎风面逐渐变为侧风面(工况5)、背风面(工况9)，压力系数分布也随之变化，由压力(正压区)逐渐变为吸力(负压区)，在来流区(0°～60°)由于流场分布比较规则均匀，压力系数随风向角的增加而逐渐降低，在侧向绕流区和尾流区(60°～180°)由于涡旋生成、脱落的不规则性，压力系数分布也呈现不规则变化趋势(如参考线A、G)。此外，对于工况4，虽然参考线A、G所在面仍处于来流区，但由于其与流场方向的夹角过大，使得该面上形成微小涡旋而产生负压区，但压力系数相对其它参考线要小得多。

表3 工况1的绕流特征值Table3 Flow characteristic dimensions of the case 1

表4 交汇点绕流特征值(2.0s)Table5 Flow characteristic dimensions of the intersection points at 2.0s

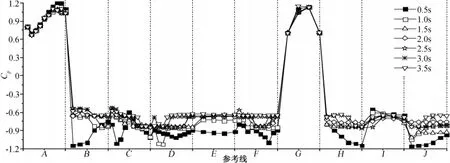
图13 工况1的平均压力系数分布Fig.13 Mean pressure coefficients of case 1

图14 平均压力系数分布Fig.14 Mean pressure coefficients

图15显示了工况1各面参考线的脉动风压分布情况。可见，脉动风压系数直接反应绕流涡旋运动的强烈程度，涡旋运动越强烈，脉动压力系数也越大，如钝体负压面的脉动压力系数均高于正压面，说明脉动风压反映钝体表面压力脉动能量的大小，对正确认识钝体表面脉动特性具有参考价值。

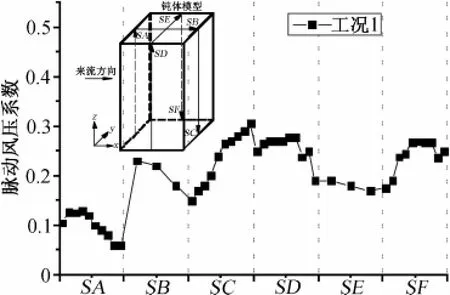
图15 脉动风压系数分布Fig.15 Fluctuating pressure coefficients

5 结论

针对三维矩形钝体采用大涡模型进行了数值模拟，再现了钝体绕流的冲撞、分离、重附着等现象，揭示了钝体绕流主、次涡循环区的形成、发展机理，得到以下结论:

(1)矩形钝体对来流区0.25、屋顶区0.4、尾流区2.0内流场的影响最大，对中心区域流场的影响要大于两侧流场，影响程度由中心向两侧逐渐减小，且其强弱程度依次为尾流区、屋顶区、来流区。

(2)来流区风场与钝体建筑物之间的绕流特性比较稳定，同一工况下任一切平面的绕流特征值随时间基本无变化，但不同切平面的绕流特征值不同，由中心向两侧逐渐减小。钝体与风场垂直时，其对尾流的影响最大;呈45°时对尾流的影响最小。

(3)尾流涡旋的非对称生成、脱落使钝体左右两侧流场与钝体之间形成不对称的冲撞、分离与重附着现象，导致钝体两侧形成不平衡压力分布，是结构产生横风向振动的重要原因。

(4)当风场与钝体垂直时，迎风面竖向压力系数均呈现由大变小再逐渐增大并在顶部再次回落的变化趋势，最大值出现在变向点附近，而其余工况下虽压力系数亦有类似结论，但压力系数值相对较小。脉动风压系数直接反应绕流涡旋运动的强烈程度，涡旋运动越强烈，脉动压力系数也越大。

［1］SELVAN N R.Computation of pressures on texas tech university building using large eddy simulation［J］.Journal of Wind Engineering and Industrial Aerodynamics，1997，67＆68:647-657.

［2］TUTAR M，OGUZ G.Large eddy simulation of wind flow around parallel buildings with varying configuration［J］.J.Fluid Dynamics Research，2002，9:289-315.

［3］MURALAMI S，MOCHIDA A.On turbulent vortex shedding flow past2D square cylinder predicted by CFD［J］.Journal of Wind Engineering and Industrial Aerodynamics，1995，54(3):191-211.

［4］YU D H，ASHAN K.Numerical simulation of flow around rectangular prism［J］.Journal of Wind Engineering and Industrial Aerodynamics，1997，67(2):195-208.

［5］CHENG Y，LIEN F S，YEE E，SINCLAIR R.A comparison of large eddy simulation with a standard k-εReynolds-averaged Navier-Stokes model for the prediction of a fully developed turbulent flow over a matrix of cubes［J］.Journal of Wind Engineering and Industrial Aerodynamics，2003，91:1301-1328.

［6］SHAH K B，FERZIGER J H.Large-eddy simulations offlow past a cubical obstacle［R］.Thermosciences Division Report TF-70.Department of Mechanical Engineering，Stanford U-niversity，1996.

［7］SHAH K B，FERZIGER J H.A fluid mechanician＇s view of wind engineering:large-eddy simulation of flow past a cubical obstacle［J］.Journal of Wind Engineering and Industrial Aerodynamics，1997，67＆68:211-224.

［8］HEE C L，THOMAS T G，CASTRO I P.Flow around a cube in a turbulent boundary layer:LES and experiment［J］.Journal of Wind Engineering and Industrial Aerodynamics，2009，97:96-109.

［9］李正良，石承启，赵仕兴，魏奇科，刘红军.复杂体型高层建筑风洞试验及数值模［J］.土木建筑与环境工程，2009，31(5):69-73.

［10］王小华，朱文芳，何钟怡.方形钝体受限绕流的三维数值模拟［J］.计算力学学报，2008，25(5):671-675.

［11］吴文权.流体绕多个钝体不稳定分离流动数值仿真［J］.工程热物理学报，1997，19(3):1-8.

［12］陈斌，郭烈锦，杨晓刚.圆柱绕流的离散涡数值模拟［J］.自然科学进展，2002，12(6):964-969.

［13］GERMANO M，PIOMELLI U，MOIN P，CABOT W H.A dynamic subgrid-scale eddy viscosity model［J］.Phys.Fluids A，1991，3(7):1760-1765.

［14］LEONARD B P.A stable and accurate convective modeling procedure based on quadratic upstream interpolation［J］.Comput.Meth.Appl.Mech.Eng，1979，19:59-98.

［15］LAATARAD A H，BENAHMEDB M，BELGHITHC A，QUERE P L.2D large eddy simulation of pollutant dispersion around a covered roadway［J］.Journal of Wind Engineering and Industrial Aerodynamics，2002，90:617-637.

［16］ADINA R ＆ D，Inc.ADINA theory and modeling guide volume III:ADINA CFD ＆ FSI［M］.USA，2005.http://www.adina.Com.

［17］BAETKE F，WERNER H.Numerical simulation of turbulent flow over surface-mounted obstacles with sharp edges and corners［J］.Journalof Wind Engineering and Industrial Aerodynamics，1990(35):129-147.

［18］BEKELE S A，HANGAN H.A comparative investigation of turbulent of the TTU pressure-numerical versus laboratory and full scale results［J］.Wind and Structures，2002，5(2-4):337-346.

［19］AIANNUZAI P S.Artificial wind generation and structural response［J］.Journal of Structural Engineering，ASCE，1987，113(10):2382-2398.

［20］WANG D Y，ZHOU Y，DENG X S，CHEN L.Numerical simulation of fluctuating wind field for high-rise buildings considering spatial correlation［A］.ISSEYE-10［C］，Beijing:Science Press，2008:1618-1624.

［21］JEONG S H，BIENKIEWICZ B.Application of autoregressive modeling in proper orthogonal decomposition of building wind pressure［J］.Journal of Wind Engineering and Industrial Aerodynamics，1997，69-71:685-695.

［22］Architechtural Institute of Japan.AIJ recommendations for loads on building［S］.2004.

［23］CASTRO I P，ROBINS A G.The flow around a surfacemounted cube in uniform and turbulent streams［J］.J.Fluid Mech.，1977，79(2):307-335.

［24］GOMES G M，RODRIGUES A M，MENDES P.Experimental and numerical study of wind pressures on irregular-plan shapes［J］.Journal of Wind Engineering and Industrial Aerodynamics，2005，93:741-756.

［25］ZHANG Y Q，HUBER A H，ARYA S P S，SNYDER W H.Numerical simulation to determine the effects of incident wind shear and turbulence level on the flow around a building［J］.J.Wind Eng.Ind.Aerodyn.，1993，46-47:129-134.