基于二次分形插值函数的分形插值曲面的变差与盒维数

黄艳丽,冯志刚

(江苏大学理学院,江苏镇江 212013)

0 前言

分形插值曲面是分形几何理论中的一个重要内容,在图形与图像处理、材料科学、地理地质科学及计算机动画仿真等领域具有广泛的应用。

在矩形区域中,一般通过构造二元迭代函数系生成分形插值曲面[1-3],但有严格的限制条件。文献[4]给出了矩形区域上分形插值曲面更加一般的连续性条件,但这一条件也过于苛刻,且在实际应用中不易判别。文献[5]中应用一元递归分形插值函数生成分形插值曲面,并给出了这类插值曲面盒维数的一个下界估计,这种方法解除了边界插值结点共线和压缩因子相等的限制条件,使得分形插值更具灵活性,更有利于实际应用。

本文研究了由二次分形插值函数生成的分形插值曲面的变差与盒维数。第 1节介绍了基于二次插值函数的分形插值曲面的构造方法;第 2节给出了连续函数中心变差的概念,以及连续函数图像的盒维数的计算公式;第 3节研究了分形插值函数的中心变差的性质,对分形插值曲面的的中心变差进行了估计,并利用二元连续函数的中心变差与其图像计盒维数之间的关系,得到了分形插值曲面的计盒维数。

1 基于二次分形插值函数的分形插值曲面的构造

设I=[0,1],J=[0,1],△={(xi,yj,zij):i=0,1,…,N;j=0,1,…,M}为I×J上的插值结点,其中,0=x0＜x1＜…＜xN=1;0=y0＜y1＜…＜yM=1。记Ii=[xi-1,xi],Jj=[yj-1,yj]和K= J×R。对于i=0,1,2,…,N,假设ui(y),y∈J,分别是过插值结点△xi={(xi,yj,zij):j=0,1,2,…,M}的一组连续函数。现给定压缩因子集S={s1,s2,…,sN},其中,＜1,i=1,2,…,N。

固定y∈J,对于i=1,2,…,N,令Fy,i(x,z)=siz+by,ix2+cy,i满足条件:

定义映射wy,i:K→K,

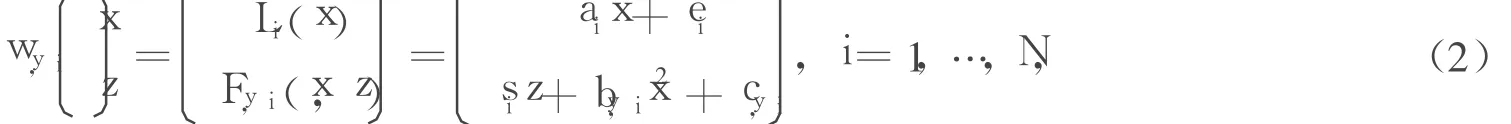
其中,ai=xi-xi-1;ei=xi-1。由条件(1)可得:

易证 wy,i在此度量下是压缩映射。则由文献[6]可得下面的定理。

定理1 对y∈J=[0,1],{K,wy,i,i=1,2,…,N}构成双曲迭代函数系,且存在I上的连续函数fy,使得fy的图像Γ(fy)={(x,fy(x))}是迭代函数系{K,wy,i,i=1,2,…,N}的不变集,即Γ=∪wy,i(Γ),并且fy(xi)=ui(y),i=1,2,…,N,称fy是对应于{K,wy,i,i=1,2,…,N}的二次分形插值函数。

定义函数F:[0,1]×[0,1]→R,使得F(x,y)=fy(x)。 (4)

引理1[7]设fy、fy′分别为过插值集△y={(xi,y,ui(y)):i=0,1,…,N},△y′={(xi,y′, ui(y′)):i=0,1,…,N}的分形插值函数,且有相同的压缩因子S={s1,s2,…,sN},则:

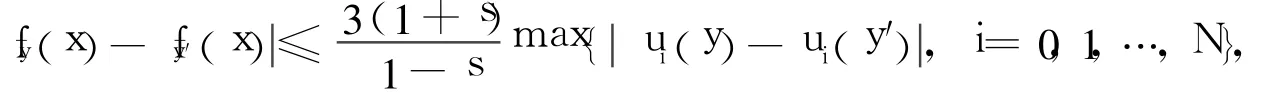
引理2 F为式(4)定义的二元连续函数,则F连续。

又ui连续,则＜δ2时,∀ε＞0, max{＜) ε。所以,

2 连续函数的中心变差与计盒维数公式

连续函数的变差是量化函数图像粗糙性质的一个重要参数,对于变差的性质及它与分形维数的关系有了较多的研究,参见文献[8-9]。为了方便以后的研究,下面给出中心振幅与中心变差的定义。

设D={ξ=(ξ1,ξ2,…,ξn):ai≤ξi≤bi,i=1,2,…,n}⊂Rn,任给ξ∈D,令

D[ξ;δ1,δ2,…,δn]=D∩([ξ1-δ1,ξ1+δ1]×[ξ2-δ2,ξ2+δ2]×…×[ξn-δn,ξn+δn])。

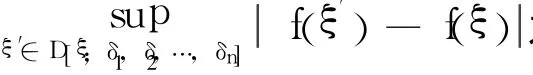
由振幅的定义,显然振幅与中心振幅有下面关系:

容易得到计盒维数与中心变差的关系。

定理2 设Γ(f,D)是连续函数f的图像,则:

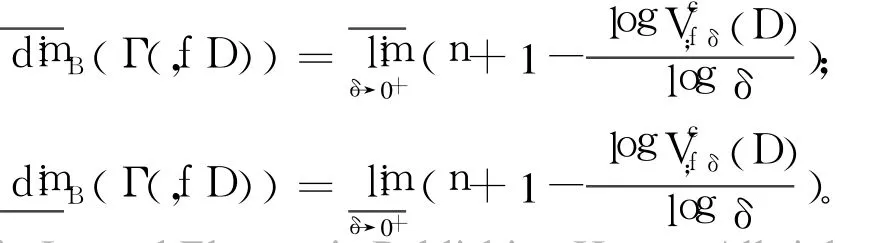
3 二元分形插值函数的中心变差与计盒维数

引理3 设fy是定理1确定的分形插值函数,则(I)在J上关于y连续。

证明 Γ={fy:y∈J}⊂C([0,1])在＜C[0,1],∞＞上紧,则 Γ等度连续,即对每一x0∈I, ε＞0,∃δ＞0,若＜δ,对∀y∈J,

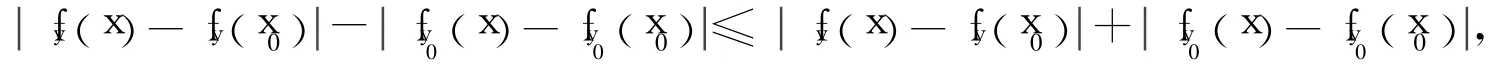
引理4 若对于某一yc∈J,插值结点{xi,ui(yc),i=0,1,…,N}不共线,则存在闭区间[a,b]⊂J,对于任意y∈[a,b],插值结点{xi,ui(y),i=0,1,…,N}均不共线。

证明 因为{xi,ui(yc),i=0,1,…,N}不共线,存在i0∈{1,…,N-1},使得h(yc)≠0,其中, h(y)=ui0(y)-[u0(y)+(uN(y)-u0(y))xi0]。由于ui0(y)、u0(y)和uN(y)均为区间J上的连续函数,从而h(y)在J上也连续。因此,存在闭区间[a,b]⊂J,对于任意y∈[a,b],函数h(y)≠0。所以,当y∈[a,b]时,点集{xi,ui(y),i=0,1,…,N}均不共线。引理证毕。

定理3 F是由式(4)定义的二元连续函数,对于任意0≤a＜b≤1有:

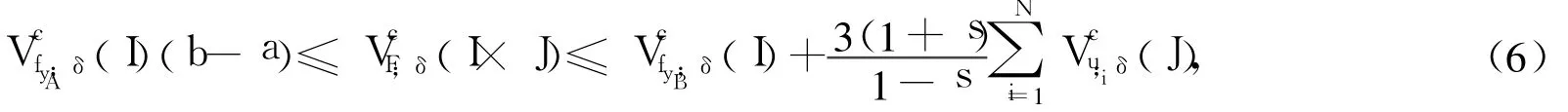
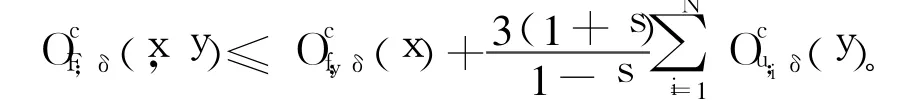
则:

定理4 F∶[0,1]×[0,1]→R是连续函数,Γ(F,D)是它的图像,设max dimB(fy)=d1,y∈J, max{dimB(ui),i=1,2,…,N}=d2且d1≥d2,则:

再由定理2和定理3得:

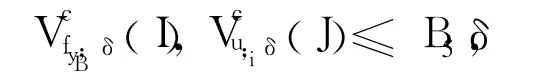
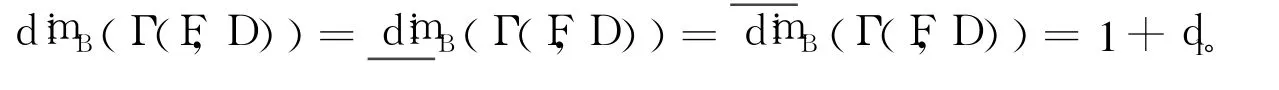
[1] Robert M.The MinkowskiDimension of the Bivartiate Fractal Interpolation Surfaces[J].Chaos,Solition and Fractal,2006, 27:1147-1156.

[2] 徐惠,冯志刚.一类分形插值函数的变差和计盒维数[J].安徽工业大学学报,2008,25(4):444-447.

[3] 江镅,冯志刚.一类多参数分形插值曲面[J].成都信息工程学院学报,2009,24(6):616-618.

[4] Feng Zhigang.Variation and Minkowski Dimension of Fractal Interpolation Surface[J].Journal of Mathematical Analysis and App lication,2008,345(1):322-334.

[5] Bouboulis P,Dalla L.Fractal Interpolation Surfaces Derived from Fractal Interpolation Functions[J].JournalofMathematical Analysis and App lication,2007,336:919-936.

[6] 沙震,阮火军.分形与拟合[M].杭州:浙江大学出版社,2005.

[7] Feng Z,Xie H.On Stability of Fractal Interpolation[J].Fractals,1998,6(3):269-273.

[8] 文志英.分形几何的数学基础[M].上海:上海科学技术出版社,2000.

[9] 冯志刚,王磊.分形插值函数的δ-变差的性质[J].江苏大学学报:自然科学版,2005,26(1):49-52.