基于共模电流频谱能量的共模干扰抑制研究
2011-04-05章勇高高彦丽龙立中
章勇高,高彦丽,龙立中
(华东交通大学电气与电子工程学院,江西南昌 330013)
0 前言
随着电力电子装置中高速开关器件的大量使用带来严重的电磁干扰问题[1-3]。在单相全桥逆变器中若采用双极性调制技术,由于两桥臂中点产生的共模电压大小相等方向相反,它们产生的共模电流相互抵消,此时逆变器产生的总共模电流为零,能够完全消除逆变器的共模电磁干扰[4]。然而,对于如单相半桥、三相、单极倍频调制的单相全桥逆变器等不存在两个互补对称共模噪声源的场合,则可以采取外加专门的补偿电路,使补偿电路产生大小相等、方向相反的补偿电流,以实现并联有源 EMI抑制。
图1所示为单相半桥逆变器的有源并联共模电磁干扰抑制的原理结构图。在图1中,Cg为桥臂中点的对地杂散电容;CO为补偿桥臂外加输出电容;C为穿芯电容;Tcm为共模变压器;R为共模电流检测电阻。桥臂共模电流通路为VA-Cg-C-Tcm,补偿电流通路为VO-COC-Tcm。Tcm和R将共模电流转化为电压VCM,通过VCM评估共模电流大小,从而调整补偿电路的控制。
并联EMI抑制原理是:通过调整补偿电路的PWM,使得VO与VA大小相等方向相反,在保证CO=Cg的前提下,总的共模电流将对消为 0。补偿过程如下:根据逆变器桥臂PWM信号VG1和VG2可以得到桥臂中点电压VA,为实现完全对消,相应的可知补偿输出电压 VO,从而决定了补偿电路的PWM信号。
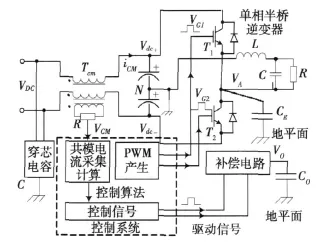
图1 半桥逆变器的有源并联共模电磁干扰抑制
然而,由于 PWM信号传输时间与电路有关,不能保证完全一致,存在时间差,且功率器体的动态特性或多或少存在个体差异,导致实际上的 VA和 VO跳变与理想有一定的差距,当然可以离线调整[4],但现实不可行。因此,有必要研究总共模电流与传输时间差之间的关系。本文通过分析不同评估指标,从表征特点与计算方面说明共模电流能量为一种最佳的共模电流评估指标,该结论得到仿真和实验验证。
1 电磁干扰共模电流评估
电磁干扰测试中,通常通过分析共模电流的频谱来评估共模干扰大小[5-7]。在闭环控制系统中要求反馈量最好为一单值函数,在频谱特性中常用的两个单值指标是频谱最大值和频谱平均值。
共模电流频谱最大值是在整个频段中出现的最大值,因此,它只能反映某一频点上的共模电流大小,当存在多个频谱峰值时,频谱最大值就不能很好的反映共模电流的总体水平。共模电流频谱均值是在整个频段范围内的平均值,能较好反映共模电流的总体水平,但当存在较大的谐振峰,频谱均值不能较好地反映这些谐振峰。此外,两者的计算都需要用快速傅里叶变换,其计算量较大。在电磁兼容设计中需要在每个频段点都能够满足要求,不仅代表了总体水平,而且也照顾特殊异常频点,故频谱最大值和频谱均值都不是一个理想的共模电流评估指标。
在频谱特性分析中,频谱能量也是一个重要的指标,首先分析一个开关周期时间内的共模电流能量。其数值定义为:一个有限能量信号的能量等于其快速傅里叶变换频谱中各次频率成分的幅值平方和。从定义可以看出:幅值较大的频点在频谱能量占更大的权重比例,可以得到很好的体现,而且可以反映整个频段的总体水平。故相对频谱最大值和频谱均值来讲,频谱能量更加适合作为共模电流大小的单值评估指标。
一个开关周期内的共模电流频谱能量仅能反映该周期内两个孤立共模电流脉冲的频谱能量,然而开关过程是一直持续的且脉冲宽度是变化的。因此,下面从理论上说明单个周期内的频谱能量完全可以表征整个电网周期内的能量。假设一个周期内共模电流的频谱表达式为:

其中,An、θn为相应频点的共模电流幅值和相位。总共模电流频谱为多个波形相同但相位不同的单开关周期内共模电流频谱的相加。假设 C为载波比,则 1个电网周期内含有 C个开关周期,其共模电流如式(2)所示。
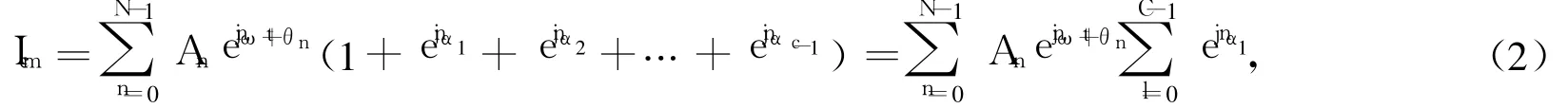
式中,a0aC-1分别为第C个共模电流的相角。考虑共模电流最严重的情况,令a0=a1=…=aC-1=0,此时各个周期共模电流相位不变,式(2)变为:

对比式(1)和式(3),总共模电流频谱幅值为单周期频谱幅值的C倍。因此总共模电流频谱能量为:

式中,εcm为单周期频谱能量;εcm∑为总频谱能量。它们为正比关系,闭环控制系统的共模电流评估反馈只需相对大小,两者都可以使用。因此,一个开关周期内的共模电流频谱能量(以下简称频谱能量)是一个理想的共模电流大小评估指标。
2 仿真研究
以上是理论分析共模电流评估指标,本节通过仿真研究证明频谱能量能否方便应用于补偿电路PWM信号调整的控制。桥臂中点电压和补偿电路输出电压以高频 PWM信号模拟,传输时间差以延时模块代替,共模电流等效流通路径以RLC二阶电路模拟,仿真原理如图2所示。在图2中,icm1、icm2和icm分别为逆变器共模电流、补偿电流以及总共模电流。参数设置如表1所示,RLC振荡频率为160 kHz。
改变延时模块时间参数就能改变 PWM信号时间差,为了更好的说明频谱能量的优越性,同时比较了频谱最大值、频谱均值和频谱能量与传输时间差中间的关系。本文通过改变RLC2的参数仿真3种不同工况下的工作情况。
工况1:逆变器共模电流与补偿电流仅仅存在相位差,此时RLC1和RLC2的参数完全相同。连续调整延时模块 2中的滞后时间参数,在 2个振荡周期内往正负方向均匀变化 80步,正方向为时间差滞后,负方向代表时间差超前。计算每一时间差下频谱能量、频谱均值和频谱最大值,绘制它们与时间差之间的关系曲线,仿真计算结果如图3所示。在图3中,横坐标表示时间差,纵坐标分别为频谱最大值、频谱均值和频谱能量,以下图4和图5同样表示。

图2 共模电流评估仿真研究模型

表1 仿真设置参数
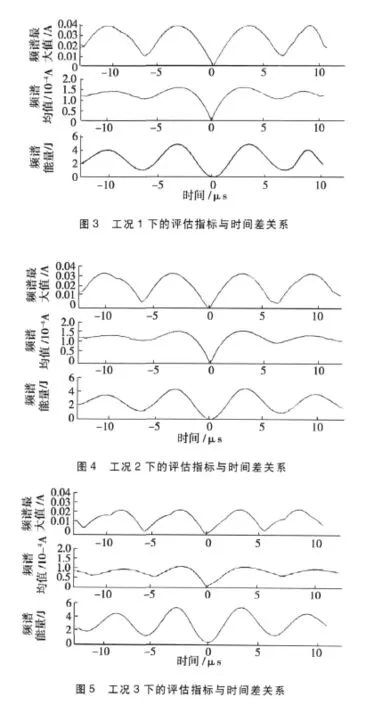
从图3可以看出:频谱最大值、频谱均值和频谱能量关于时间差为 0对称振荡,振荡周期与RLC振荡周期一致。当时间差为RLC振荡周期整数倍时,三者均为极小值;当时间差为RLC振荡周期整数倍的一半时,三者均为极大值。然而,频谱最大值和频谱均值的极值大致不变,频谱能量却在整个仿真时间差内呈现对称衰减振荡特性,即频谱能量极大值随时间差增大而降低,极小值随时间差增大而提高。
工况2:逆变器共模电流与补偿电流不仅存在相位差,而且存在波形失真,表现为单纯的幅值不同。即两电流的振荡频率一样,因此可以通过调整RLC2中的电阻实现,仿真中设置为 200Ω。仿真过程与工况1一致,仿真结果如图4所示,图4中各个指标参数的特征与图3基本一致。
工况3:逆变器共模电流与补偿电流不仅存在相位差,而且存在波形失真,表现为振荡频率不同。可通过调整RLC2中的电容电感实现,本仿真中设置为C=0.818 nF,电阻和电感参数不变,此时补偿电流振荡频率为176 kHz,逆变器共模电流 160 kHz。仿真过程与上述一致,仿真结果如图5所示。
从图5可以看出:频谱最大值和频谱均值不再呈现对称振荡的特征,而频谱能量还基本上呈现对称振荡特性,不过不再关于时间差为 0对称,但并不影响其评估共模电流大小的效果。因此,从仿真结果分析可得出结论:共模电流频谱能量与PWM信号时间差之间的对称衰减振荡特性与工况基本无关,可以作为理想的共模电流评估指标。
3 实验研究
建立单相半桥逆变器的有源并联补偿物理实验模型[7],模型的结构与图1一致。实验模型以DSP为控制器,补偿电路为P-MOSFET构成的推挽电路,DSP采集并计算共模电流频谱能量,根据仿真结果的对称衰减振荡特性,利用智能搜索算法[9]调整补偿电路PWM信号,使得补偿电流和逆变器共模电流完全对消。为了说明调整效果,文中比较了调整前后逆变器总共模电流的时域波形和频域波形,如图6和图7所示。
从图6所示的时域波形可以看到:调整前共模电流较大,幅值约为0.20.35 A,调整后变为约0.10.2 A,从波形对比来看,调整效果是明显的。

由图7的频域波形可知:调整后的逆变器频谱特性得到了较大的改善,在150 kHz10MHz的效果比较明显,整体上下降了1015 dBμV。然而,本补偿电路在高于10MHz的频率范围内没有什么效果,其原因在于硬件电路(包括补偿电路和信号处理电路)的带宽影响,不过从实验结果来看,逆变器共模电流在高于10MHz范围内本身就很小。所以,从总体上来讲,调整前后共模电流得到了很好的抑制,同时,说明了共模电流频谱能量的评估指标在共模干扰抑制系统有效性。
4 结论
在有源并联共模电磁干扰抑制中,PWM信号传输时间差将导致补偿电路的输出电压与桥臂中点电压不能完全保证严格的反相,使得补偿电流与共模电流完全对消,从而大大影响共模电磁干扰的抑制效果,需要通过共模电流的大小来相应的调整补偿电路的PWM信号。
共模电流频谱能量、频谱最大值和频谱均值均为电磁兼容研究中评估指标,频谱最大值和频谱均值需要复杂的傅里叶计算使得其不适合用于逆变器的控制中,而频谱能量的计算简单而且在不同补偿工况下均能较好的反映共模电流大小与 PWM信号传输时间差之间的关系。通过 3种不同工况下的仿真研究说明了频谱能量与传输时间差之间呈现对称衰减振荡特性,能够较好的应用于补偿电路 PWM信号的调整控制系统中,是理想的共模电流评估指标。
建立单相半桥逆变器的有源共模电磁干扰抑制物理实验模型,从时域波形和频域波形都验证了调整的补偿效果,进一步说明共模电流频谱能量在有源共模电磁干扰抑制中的有效性和实用性。
[1] Laszlo T.Electromagnetic Compatibility in Power Electronics[M].New York:IEEE Press,1995.
[2] Liu Q,Wang D,Boroyevich F.Frequency-domain EMI Noise Emission Characterization of Switching Power Modules in Converter Systems[C]//20th Annual IEEE Applied Power Electronics Con ference and Exposition,APEC2005.USA: IEEE,2005:787-792.
[3] 咸哲龙,钟玉林,孙旭东,等.用于传导电磁干扰分析的接地回路模型与参数[J].中国电机工程学报,2005,25(7): 156-161.
[4] 张凯,周运斌,章勇高,等.基于驱动脉冲自校准的全桥电路共模抑制技术[J].中国电机工程学报,2007,27(13): 58-63.
[5] 和军平,陈为,姜建国.电源线EMI滤波器内部杂散电磁耦合及其作用[J].电工技术学报,2006,21(10):12-17.
[6] Un E,Hava A M.Performance Analysis and Comparison of Reduced Common Mode Voltage PWM and Standard PWM Techniques for Three-phase Voltage Source Inverters[C]//The Twenty-first Annual IEEE Applied Power Electronics Conference and Exposition,APEC'06.USA:IEEE,2006:303-309.
[7] 章勇高,高彦丽,张凯.抑制共模电磁干扰的并联有源补偿电路设计[J].电工电能新技术,2008,27(4):90-94.
[8] Dunham J.Fourier Series and Orthogonal Polynom ials[M].New York:Dover Publications,2004.
[9] Zhang Y G,Zhang K,Zhou Y B,et al.Common Mode EMISuppression Based on Simulated Annealing Algorithm[C]//Proceedings of the 6th WCICA 2006.China,2006:8448-8452.
