三维抛物型方程的紧交替方向差分格式

陈贞忠 ,马小霞

(1.新乡学院数学系,河南新乡 453000;2.焦作大学基础部,河南焦作 454003)

0 前言

近期出现了许多求解抛物型偏微分方程的差分格式[1-8],但交替方向法仍然是求解二维和三维抛物型方程比较理想的数值方法。该法的最早提出者是Peaceman和Rachford,他们提出了二维问题的PR格式[9],此后,又产生了适用于二维和三维问题的 Douglas格式[10],所有这些格式的精度都较低,截断误差仅为O(τ2+h2)。

本文对三维常系数非齐次抛物型方程的初边值问题

导出了一个高精度恒稳定的紧交替方向差分格式,截断误差阶达到O(τ2+h4)。然后,使用外推算法得到了O(τ3+h6)阶精度的近似解,实验结果与理论分析完全相符。

1 差分格式的建立与截断误差

将求解区域进行网格剖分。设τ=△t为时间步长;h=△x=△y=△z为空间方向步长;为在节点(jh,kh,lh,nτ)处的网函数值,方程(1)的解函数为u(x,y,z,t)。

记u(jh,kh,lh,nτ)=u(j,k,l,n),由Taylor展开可得:

由式(4)和式(5)得(1-▽t)-1=exp(τ),从而 τ=-ln(1-▽t),即:

在(j,k,l,n+1)处考虑方程(1)有:

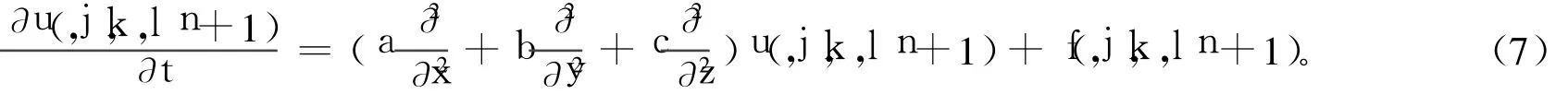
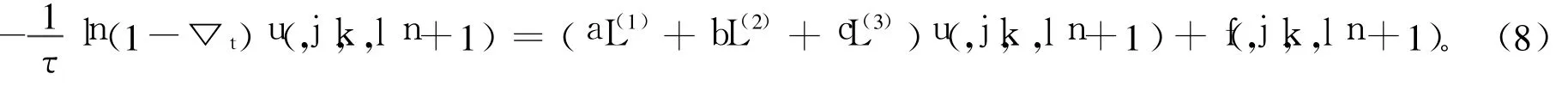
构造如下4个差分算子:

取η0=,则有:

故当η0=时,式(9)成立。取η1=,则有:

同理取η2=η3=2 ,则有:

式(16)左端可以化为:

式(16)右端可以化为:

由于:

则式(16)可化为:

可得方程(1)的差分格式:

可知格式的截断误差为ο(τ2+h4)。

2 紧交替方向算法

式(19)可分解为:

观察交替方向算法(20)在每个时间层上只需用追赶法解 3个三对角的方程组,因此计算量较小。

3 差分格式的稳定性与收敛性

利用Fourier稳定性分析方法,令:

将上式代入格式(20)的误差方程,即式(20)的齐次形式中,经计算整理,并利用关系式

根据s1的取值范围可知:

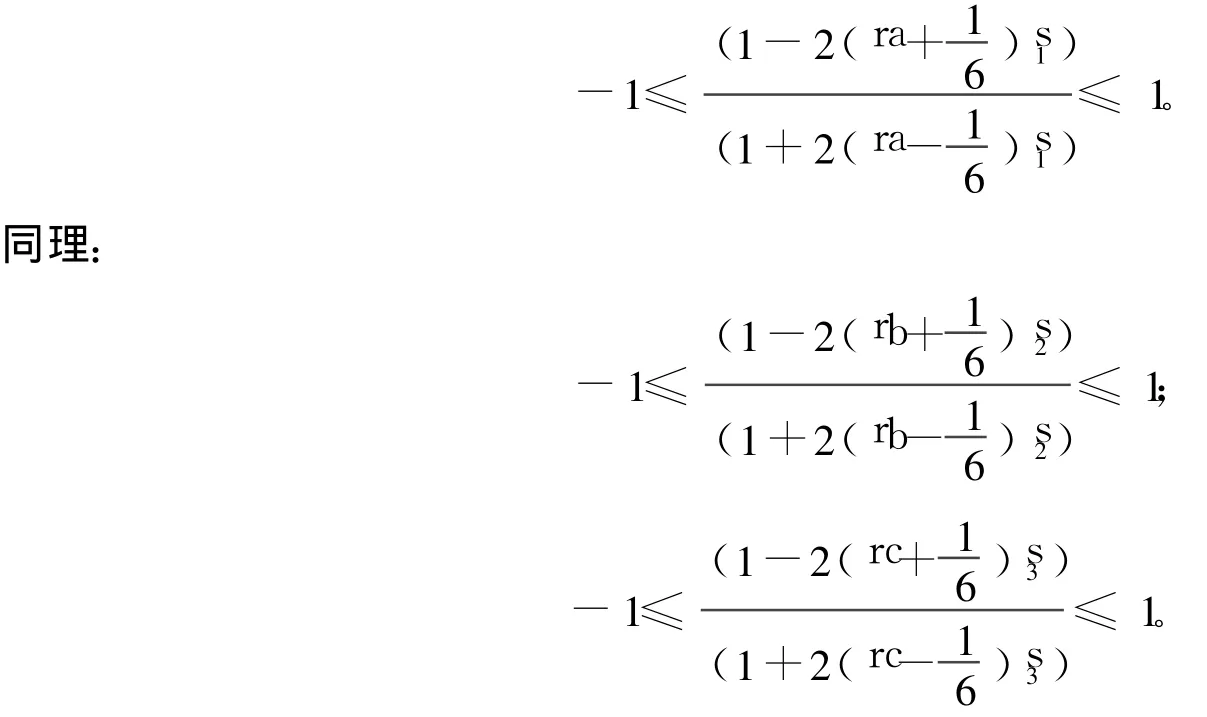
定理 紧差分格式(20)绝对稳定且以ο(τ2+h4)的收敛阶收敛。

4 外推算法

为了提高格式(20)的数值解的精度,使用Richardson外推法,根据前边的论述知:

5 数值实验

在区域D:{0≤x,y,z≤1,t≥0}上对初边值问题:

用本文格式(20)和三维问题的Douglas格式[11]求数值解,并与精确解u(x,y,z,t)=e-4tsin(x+y+z)相比较,取h=1/10;τ=rh2=r/100;r=1/2,1,计算到n=200时的结果见表1。

表1 各种算法计算结果与精确解数值比较表

由表1可以看出:本文格式(20)解与精确解均有较好的吻合,它较文献[11]中的Douglas格式至少精确 2位有效数字,本文格式(20)外推一次所得数值结果与精确解至少有 9位有效数字吻合,这与理论分析一致。

[1] 曾文平.多维抛物型方程的分支绝对稳定的显格式[J].高等学校计算数学学报,1997,19(2):112-121.

[2] 马明书.解三维抛物型方程的一个新的高精度显格式[J].应用数学和力学,1998,19(5):65-469.

[3] 孙鸿烈.解高维热传导方程的一族高精度显式差分格式[J].高校应用数学学报:A辑,1999,14(4):427-432.

[4] 马明书,王同科.三维抛物型方程的一族高精度分支差分格式[J].应用数学和力学,2000,21(10):1087-1092.

[5] 刘继军.二维热传导方程的三层显式差分格式[J].应用数学和力学,2003,24(5):537-543.

[6] 李雪玲,孙志忠.二维变系数反应扩散方程的紧交替方向差分格式[J].高等学校计算数学学报,2006,28(1):83-95.

[7] 马菊意,杨辉.二维抛物线方程的一个高精度PC格式[J].工程数学学报,2008,25(2):373-376.

[8] 马明书,王晓峰,马文娟.二维变系数非齐次抛物型方程的紧交替方向差分格式[J].河南科技大学学报:自然科学版,2008,29(3):88-90.

[9] Peaceman DW,Rachford JH H.The Numerical Solution of Parabolic and Elliptic Differential Equations[J].J Soc Ind Appl Math,1959,3:28-41.

[10] Douglas JJ.Alternating Direction Methods for Three Space Variables[J].Numer Math,1961(4):41-63.

[11] 胡健伟,汤怀民.微分方程数值解[M].北京:科学出版社,1999:229-240.