基于EMD分解和支持向量机的齿轮箱故障诊断与研究

（中北大学机械工程与自动化学院，太原030051）

基于EMD分解和支持向量机的齿轮箱故障诊断与研究

刘晓娟，潘宏侠
（中北大学机械工程与自动化学院，太原030051）

齿轮箱存在故障时，其振动信号往往表现出非平稳特性，并且故障特征信息往往淹没在强大的背景噪声中，难以实现有效诊断。提出了采用基于EMD方法的特征能量值提取法及支持向量机的智能模式诊断方法，并将二者结合运用于齿轮箱的故障诊断，实现了齿轮箱故障的智能识别与诊断。实验结果证明了EMD方法与支持向量机相结合用于齿轮箱故障诊断的正确性与可行性。

齿轮箱故障诊断EMD支持向量机

1 引言

在科学技术水平不断迅猛发展的今天，现代工业中的机械设备正日益朝着结构复杂化、过程自动化、运行智能化的方向发展。在各类机械设备中，由于齿轮箱具有传动力矩大，结构紧凑等特点，成为了机械设备中主要的传动设备之一，在航空工业、农业机械、电力系统、运输机械等现代工业中得到了广泛的应用，其一旦发生故障往往会造成机器设备失效，进而造成不可估量的经济损失，乃至人员伤亡的严重后果[1]。

当齿轮箱发生故障时，其振动信号往往会表现出非平稳的特性，而且故障特征常常被强大的背景噪声所淹没，这为后期故障特征的提取和诊断的有效实现带来了很大的困难。传统的以Fourier变换为核心的信号处理方法在处理齿轮箱故障这种信噪比低、干扰强烈的非平稳信号时，效果不佳，迫切需要一种新的信号处理方法来有效实现对齿轮箱故障信号的降噪与特征提取任务[2]。本文以齿轮箱作为研究对象，主要利用EMD方法和支持向量机完成了对齿轮箱故障信号的特征提取和故障模式识别，实现了齿轮箱典型故障的诊断，体现出EMD方法与支持向量机相结合的故障诊断方法的优越性，具有重要的理论意义与实际应用价值。

2 EMD特征提取方法

EMD方法是基于信号局部特征时间尺度，能把复杂的信号函数分解为有限个固有模态函数（IMF）之和，每个固有模态函数都表示了原始信号的一个固有振动模态，它们很好地体现了信号的局部特性[3]。其分解从本质上讲是对一个非平稳信号进行平稳化处理，将信号中不同尺度的波动或趋势逐级分解出来，产生一系列具有不同特征尺度的数据序列，每一个序列成为一个固有模态函数(IMF)，它们都是平稳的。再对这些平稳的固有模态函数进行处理便可提取信号的特征信息，为机械设备的故障诊断提供依据。

2.1 EMD方法的“筛分”过程

EMD是通过一种被称为“筛分”的过程将复杂的非线性非平稳信号分解为若干个本征模态函数(IMF)与一个余项的和。它包括两部分：一是均值的求取过程，另一个是分量的提取过程。运用EMD方法将一个复杂的信号分解为若干个固有模态函数（IMF）之和，它基于这样一个基本假设：即任何复杂的信号都是由一些不同的固有模态函数组成，任何时候，一个信号都可以包含许多固有模态函数，如果模态函数相互重叠，便形成复杂信号。

采用EMD方法实现对任何信号x(t)的分解，具体步骤如下[4,5]：

（1）确定信号x(t)中所有的局部极值点，利用三次样条插值函数拟合形成信号x(t)的上、下包络线；

（2）将上包络线和下包络线的均值记作m1，求得

h1=x(t)-m1（1）

（3）判断h1是否为IMF；若h1不满足IMF的条件，把h1作为原始数据重复步骤（1），直至h1满足IMF的条件，记

c1=h1（2）

其中，c1为信号x(t)第1个满足IMF条件的分量。（4）将c1从x(t)中分离出来，得到

r1=x(t)-c1（3）

将r1作为原始数据重复步骤（1）～（3），重复循环n次，得到信号x(t)的n个满足IMF条件的分量。这样就有

当rn成为一个单调函数不能再从中提取满足IMF条件的分量时，循环结束。

这样由式（3）和式（4）得到

其中，rn称为残余函数。

EMD的分解过程就是所谓的“筛分”过程，它是从特征时间尺度出发。首先把信号中特征时间尺度最小的模态分离出来，然后分离特征时间尺度较大的模态函数，最后分离特征时间尺度最大的分量。其目的是消除模态波形的叠加并使波形轮廓更加对称。EMD方法具有自适应的特点，更适用于非线性和非平稳信号的分析处理。

2.2 基于EMD分解的特征能量提取方法

对齿轮箱进行故障诊断，关键是获得有效的特征值。EMD分解法具有自适应性，非常适合于处理非平稳和非线性信号。基于EMD的特征能量提取法，就是在EMD分解的基础上提出的一种有效提取故障特征的方法。

主要有以下几个步骤：

（1）对齿轮各种状态下的信号进行EMD分解，获得不同频率成分的IMF分量。

（2）求个频率成分的总能量。可以取前几个故障信息比较明显的特征分量，并计算各个分量的总能量。

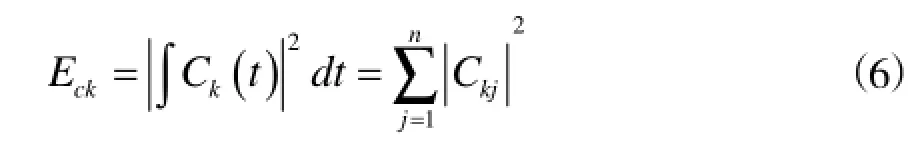
其中，Ckj（j=1，2，…）表示k层分解的第j个离散点的信号幅值。

（3）构建特征向量，并进行归一化。

对上式进行归一化处理，

归一化后的特征向量为

3 支持向量机方法

支持向量机（Support Vector Machine，SVM）是在统计学理论基础上发展起来的新的通用学习方法，其内容是在1992到1995年间基本完成的，属于统计学理论中最年轻的部分，目前仍处于不断的发展阶段。它建立在VC维理论和结构风险最小化原则基础上，具有理论严密、适应性强、全局优化、训练效率高和泛化能力好等优点，能够较好地解决小样本、非线性、局部极小等问题。

支持向量机分类算法中的模型选择问题是指对于某一给定的问题，如何寻找到最适合的核函数，其中包括核函数类型的确定、核参数的优化以及针对具体给定数据的核函数的修正等方面。模型的选择显著影响着机器泛化能力的好坏，在设计支持向量分类机时，不合适的参数选择往往会导致分类过程的失败，使分类机不能满足实际应用的要求，因此支持向量机模型的选择是SVM从理论到实际应用的关键。

在支持向量机问题表达和实现的过程中，包含几个待定的设计参数，一是核函数的种类和参数，二是正则化参数C。支持向量机参数的选择对支持向量机的学习性能影响很大，合理的参数选择可以使支持向量机具有更高的训练强度和更强的推广能力。

3.1 支持向量机分类

支持向量机分为线性支持向量机和非线性支持向量机两类：

（1）线性支持向量机

对于两类的线性分类问题，建立线性支持向量机转化为求解如下一个二次凸规划问题。

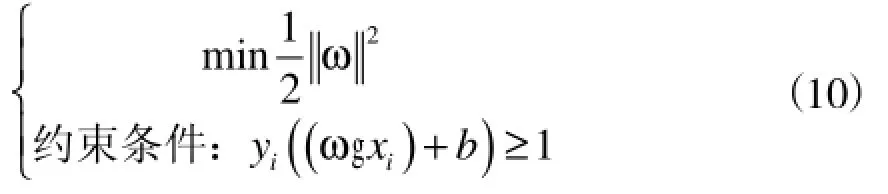
由于目标函数和约束条件都是凸的，根据最优化理论，这一问题存在唯一的全局最优解。应用Lagrange乘子并考虑满足KKT（Karush-Kuhn_Tucker）：

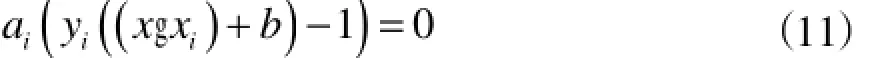
可求得最优超平面决策函数为

对于线性不可分的情况，可通过引入松弛变量ξi≥0，修改目标函数和约束条件，应用完全类似的方法求解。与（4-3）类似的新的凸规划问题为：

在上式中，若ξi都为0，上式就会变为上述的线性可分问题。上式中大于0的ξi对应错分的样本，表示允许一定的错分情况。容许错分的分类超平面称为软间隔分类超平面。

（2）非线性支持向量机

支持向量机真正有价值的用途是用来解决非线性问题。首先，原始数据经过预处理，进行特征提取，然后采用适当的核函数进行变化，通过非线性变换将输入空间的数据映射到一个高维乃至无穷维的特征空间，从而在特征空间中可以应用线性支持向量机的方法解决样本空间中的高度非线性分类和回归的问题。支持向量机算法结构如图1所示。

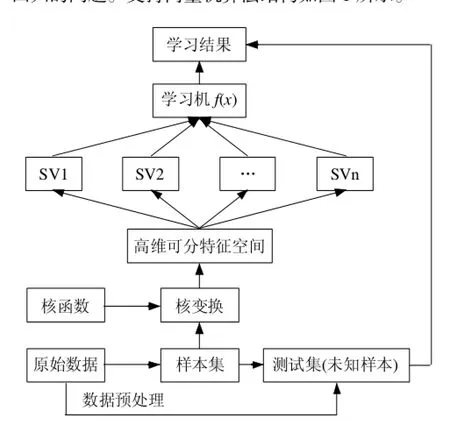
图1 支持向量机算法结构图

在特征空间F中应用线性支持向量机的方法，分类决策函数变成如下形式：

其次，利用核函数进行转换通常是隐式的，由于构造支持向量机的最后表达式是以内积的形式出现的，因此就采用内积来表达这种转换，而不是映射函数本身，这就免去了映射函数难以显示表达的问题。

3.2 核函数

支持向量机将结构风险最小化原理、对偶原理、最优化方法和核函数等几项技术有机结合在一起，有效地解决了传统机器学习方法中出现的“维数灾难”和“过学习”等困难。在解决非线性学习机器的计算能力和泛化能力方面，核函数起决定性的作用。

核函数理论很早就被提出来了，与之相关的Mercer定理更是可以追溯到1909年。支持向量机的性能在很大程度上依赖于核函数的选择，使用不同的核函数，其表现出来的性能有很大的不同，因此选择一个合适的核函数是支持向量机算法的关键[6]。

SVM中不同的内积核函数将形成不同的算法，目前研究的核函数主要有以下3种：

（1）多项式核函数

对于给定的训练样本，系统的VC维取决于多项式的次数q，因此可以通过选择合适的q值来控制系统的VC维。

（2）径向基核函数（RBF）

径向基核函数又称高斯核函数，其表达式为：

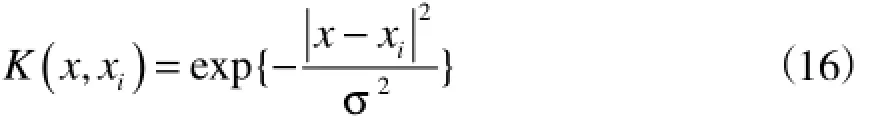
径向基函数是普遍使用的核函数，因为它对应的Hilbert空间的位数是无穷的，优先训练样本在该Hilbert空间中肯定是线性可分的。

（3）Sigmoid核函数

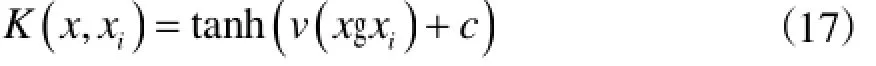
S型核函数采用双正切函数，当且仅当和取适当的数值时，这个函数才能满足Mercer条件。此式支持向量机实现的是包含隐层的多层感知器，隐层节点数由算法自动确定。

4 基于EMD和支持向量机的齿轮箱故障诊断

4.1 实验装置

本实验在JZQ-250型齿轮箱故障诊断实验台上进行，其结构如图2所示，齿轮箱由输入轴、中间轴、输出轴、2对直齿轮、3对轴承和箱体组成。输入轴经由联轴器与电机相连，输出轴与磁粉制动器连接。实验测试时输入轴转速由变频器控制电机进行调节。在输入轴、中间轴和输出轴两端轴承上方的箱体上分别安装6个测点振动加速度传感器，以测量齿轮箱运行时的振动信号。

图2 实验台组成框图

4.2 实验数据处理

分别在齿轮箱断齿和正常状态以及外圈裂纹故障3种信号中随机抽取16个样本，其中8个做为测试样本，其余8个作为训练样本。再对所测得的信号进行EMD分解，取IMF分量的前8个分量，计算各个分量的能量值，并进行归一化后将其输入到支持向量机。运用EMD能量特征提取法获得的故障特征向量训练样本和测试样本归一化后的数据如表1和表2所示。

由于齿轮箱故障类型较少，故可采用“一对一”算法，建立3个故障子分类器SVM1，SVM2，SVM3。将EMD分解后得到的特征向量值输入到支持向量机中，并采用径向基核函数，得到满意的结果。对SVM1定义y=1为正常，y=2表示断齿；对SVM2，y=2表示断齿，y=3表示外圈裂纹；对SVM3，y=1为正常，y=3表示外圈裂纹。判别采用投票决策法，结果表明SVM全部识别成功。表3给出了3种状态测试样本的识别结果，显然分类结果与实际情况完全一致。从表中可看出建立SVM故障分类器的可行性。

表1 输入向量机训练样本特征向量值

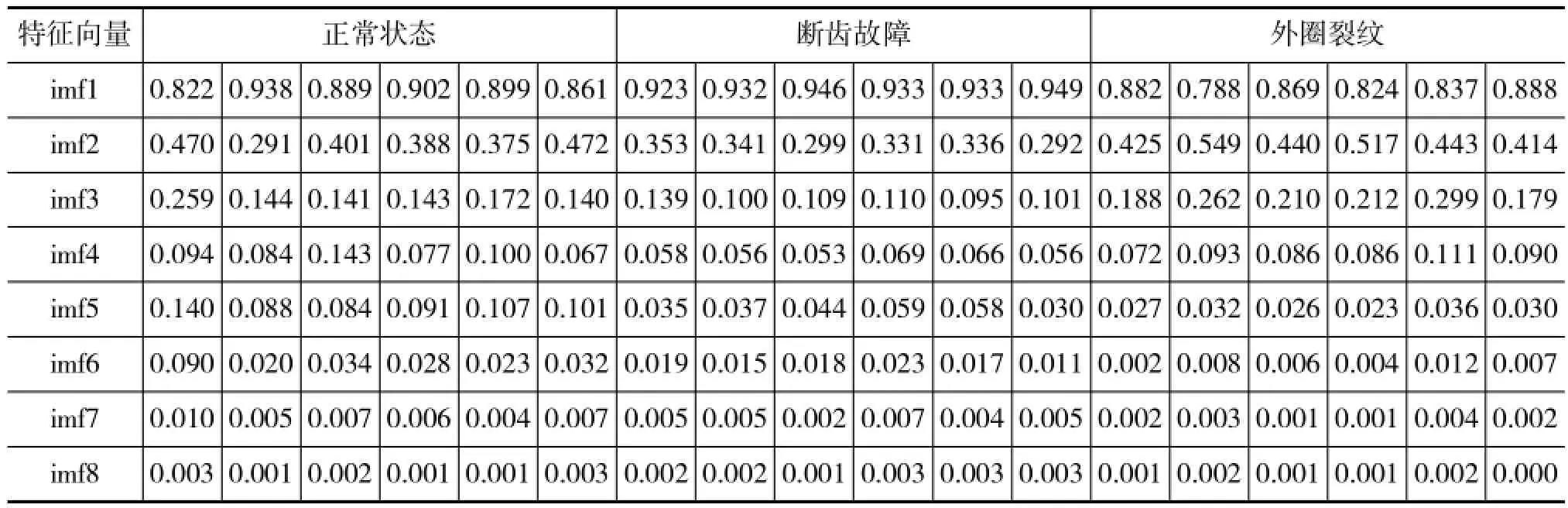
表2 输入向量机测试样本特征向量值

图3～图8为齿轮箱正常状态和各种故障状态下的时域振动信号曲线图和对应的振动信号的EMD分解图，从各种状态下信号的EMD分解图中可以看出，分量IMF的个数不相同，轴承外圈裂纹状态和断齿状态信号的IMF分量数为11，正常状态和内圈点蚀状态信号的IMF分量数为10，且由于后面的IMF分量的能量都较小，因此选取各信号IMF分量的前8个分量进行特征值计算。从图中也可以看出EMD分解法具有很好的时频特性。

表3 多分类SVM齿轮箱故障识别结果

图3 齿轮箱正常时域曲线图

5 结论

本文对齿轮箱正常状态和断齿状态下测得的信号利用EMD方法进行分解，进而用支持向量机的

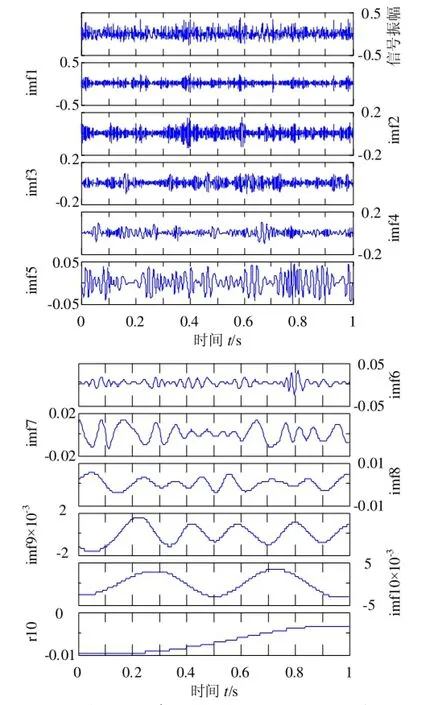
图4 齿轮箱正常状态时域信号的EMD分解

图5 齿轮箱断齿状态时域曲线图

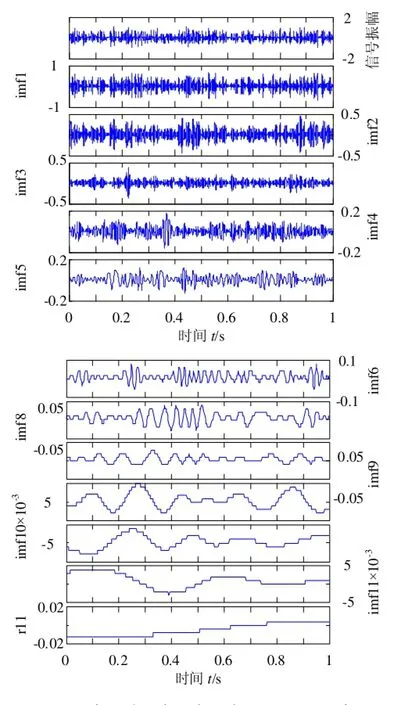
图6 齿轮箱断齿状态时域信号EMD分解

图7 齿轮箱外圈裂纹时域曲线

图8 齿轮箱外圈裂纹状态时域信号EMD分解

方法进行模式识别，证明了其有效性。由此说明，EMD分解方法与支持向量机相结合诊断方法在机械故障诊断中具有很强的现实意义。

1丁玉兰，石来德.机械设备故障诊断技术[M].上海：上海科学技术文献出版社，1994.

2 Liu B,Riemenschneider S,Xu Y.Gearbox fault Diagnosis Using Empirical Mode Decomposition and Hilbert Spectrum[J].Mechanical Systems and Signal Processing.2006(20):718-734.

3于德介，程军圣.EMD方法在齿轮故障诊断中的应用[J].湖南大学学报，2002，29(6)：48-51

4 Norden E.Huang,Zheng Shen,Steven R.Long,et al.The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-stationary Time Series Analysis[J].Proceeding of Royal Society London,1998,454(A):903-995.

5 Huang Norden E,Shen Zheng,Long Steven R,et al.A New View of Nonlinear Water Waves-The Hilbert Spectrum.[J].Ann.Rev.Fluid Mech.,1999, 31:417-457.

6魏于凡.支持向量机在智能故障诊断中的应用研究[D].保定：华北电力大学，2007.

Intelligent Diagnosis Research of Fault s in Gear Box Based on Support Vector Machines and EMD resolution method

Liu Xiaojuan,Pan Hongxia
（College of Mechanical Engineering and Automatization，North University of China,Taiyuan 030051,China）

Wh en the fault of gear box occurs,the vibration signals often show non-stationary characteristics and the fault information is often submerged in the strong background noise.This paper, based on EMD resolution method and support vector machines,is research on the techniques of the fault energy feature extraction and intelligent diagnosis of gearbox.The final result shows that the method is correct and feasible.

gearbox;fault diagnosis,EMD,support vector machines

10.3969/j.issn.1671-0614.2011.03.006

来稿日期：2010-03-23

刘晓娟（1986－），女，硕士研究生，主要研究方向为机械故障监测与诊断。