基于有限元子模型的曲轴强度及耐久性分析

（江苏江淮动力股份有限公司，江苏盐城224001）

基于有限元子模型的曲轴强度及耐久性分析

刘保林
（江苏江淮动力股份有限公司，江苏盐城224001）

针对用传统方法分析曲轴强度及耐久性时遇到的模型规模大、计算耗时长等缺点，引入了有限元子模型法并对其应用进行研究。以某单缸柴油机曲轴为例，首先使用子模型法计算曲轴各圆角在单位载荷下的应力，然后再结合载荷历程曲线计算曲轴在最大扭矩工况和额定工况的安全系数。计算过程和结果表明了用有限元子模型法分析曲轴强度和耐久性的可行性和有效性。

曲轴有限元子模型强度耐久性

1 引言

曲轴是在复杂工况下工作的，同时承受着扭转应力和弯曲应力，而且这些应力又都随时间发生周期性变化，因此有必要对曲轴的静态应力、动态应力和疲劳强度进行计算[1]。曲轴的主轴颈圆角、曲柄销圆角、油孔等局部结构都是容易发生疲劳破坏的位置，在计算分析时需要非常细密的有限元网格才能保证计算结构的准确性[2]。在对曲轴进行网格划分时，四面体单元容易生成，但精度较差，为了满足精度要求需要大大增加总单元数，导致总自由度数增加而使得计算耗时长、计算结果文件大，后处理不方便[3]；而六面体单元精度高，但需要手动进行拓扑划分网格，前处理工作量较大，甚至有时无法实现。

针对曲轴有限元计算中存在的这些问题，本文提出了基于有限元子模型的曲轴强度分析方法，仅对圆角、油孔等危险区域的网格划分成细密的六面体单元，使应力梯度较小，从而保证应力峰值和最大应力位置准确，同时有效地缩短计算时间和控制计算成本。

2 子模型的基本知识

首先简单介绍一下子模型的一些基本术语[4]：全局模型（Global model）、子模型（Sub-model）、子模型边界（Sub-model boundary）及驱动变量（Driven variable）。

对于要分析的结构的完整模型称为全局模型；将全局模型中最关心的部分切下来，称为子模型。而子模型边界是指子模型与全局模型之间具有公共特征的边或面。驱动变量一般是位移，全局模型在子模型边界上的位移结果被作为边界条件来引入子模型。如果全局模型和子模型在子模型边界上的节点分布不同，则分析程序可以对全局模型在此处的位移结果进行插值处理。图1以曲轴半拐为全局模型，将主轴颈圆角区域部分切出作为子模型，而子模型与全局模型的4个结合面定义成子模型边界。

图1 全局模型与子模型

子模型结构通常都比较简单，很容易划分成形状规则、质量好的六面体单元，并对应力集中部位进行细化。由于子模型尺寸较小，生成的单元数量少，计算快、效率高。

另外在使用子模型分析法时还要注意，全局模型在子模型边界上的位移结果是否准确，会在很大程度上影响子模型的分析结果精度。因此要保证全局模型在子模型边界上有足够细化的网格，另外还要尽量选择位移变化不剧烈的位置作为子模型边界[4]。

3 曲轴圆角子模型的静力分析

本文以某单缸柴油机曲轴为例，采用有限元子模型法分析其强度及耐久性。如图2所示，主轴颈1的直径为Φ70 mm，主轴颈2的直径为Φ75 mm，主轴颈圆角半径R3 mm，曲柄销圆角半径R4.5 mm，从左到右依次定义为MJ1、CP1、CP2和MJ2。

对图2所示的单缸柴油机曲轴需要建立4个子模型就可以完成2个主轴颈圆角及2个曲柄销圆角的强度分析。取第1主轴承中心面与曲柄销中心面之间部分为第1曲柄，曲柄销中心面与第2主轴承中心面之间部分为第2曲柄，二者独立划分网格，成为2个全局模型。

图2 曲轴三维模型

图3 中左图是第1曲柄的全局模型，用一阶四面体单元划分，单元尺寸也不需要很小，共包括32 895个单元、7 937个节点。图3中右图是第1曲柄的主轴颈圆角子模型和曲柄销圆角的子模型。为了保证计算精度，需要较高的网格密度，尤其是在圆弧段需要划分8层以上网格。用一阶六面体单元对圆角子模型划分网格，圆弧段划分了10层，每个子模型包括45 360个单元、54 720个节点。

在完成全局模型和子模型的网格建立之后，需要计算单位载荷下圆角子模型的应力，为下一步的疲劳分析提供基本的应力输入。首先以全局模型为分析对象，约束曲柄销端面节点的全部自由度，在主轴颈端面的节点上分别施加X、Y、Z、Φx、Φy、Φz六个自由度的单位位移激励，共6个载荷步；然后再约束主轴颈端面节点的全部自由度，在曲柄销端面的节点上分别施加X、Y、Z、Φx、Φy、Φz六个自由度的单位位移激励，共6个载荷步。这样共得到12个载荷步下全局模型的应力结果。

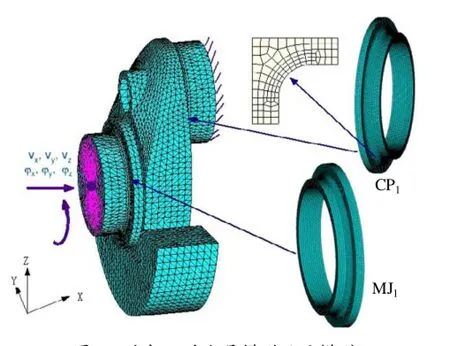
图3 曲柄1的全局模型及子模型

然后以圆角子模型为分析对象，将上面计算得到的12个载荷步的全局模型的位移结果作为圆角子模型的边界，分析后就可以得到12个载荷步下圆角子模型的应力结果。

图4是曲柄1全局模型及子模型的静力分析结果，对比后不难发现由于全局模型网格粗糙，圆角处的应力较小，应力集中并不明显，不能满足疲劳分析需求；但是圆角子模型的应力集中明显，应力梯度小，能够满足疲劳分析的要求。

图4 曲柄1全局模型及子模型的静力分析结果

4 曲轴圆角的耐久性分析

4.1 子模型的耐久性分析方法

简单的疲劳分析需要3方面的信息：几何信息、载荷信息和材料特性[5]。通过虚拟的疲劳仿真计算，可在实物样机制造出来之前就能了解整个零部件内部的应力变化及安全系数分布，从而评价结构是否满足设计要求。对于传统的虚拟疲劳仿真流程来说，除了几何信息来源于结构的有限元模型之外，一般还需要2个方面的输入：一是材料的疲劳特性参数，二是结构应力－应变的时间历程。材料参数可按照相关疲劳试验的标准从试验中获得，也可从材料手册或材料数据库软件中查得。

不同于传统的疲劳仿真分析流程，基于子模型的曲轴耐久性分析不需要结构动态应力计算结果，而是结合子模型单位载荷下的静力结果及载荷－时间历程，通过线性叠加得到一个循环内子模型的动态应力，用于耐久性分析，整个分析流程如图5所示。

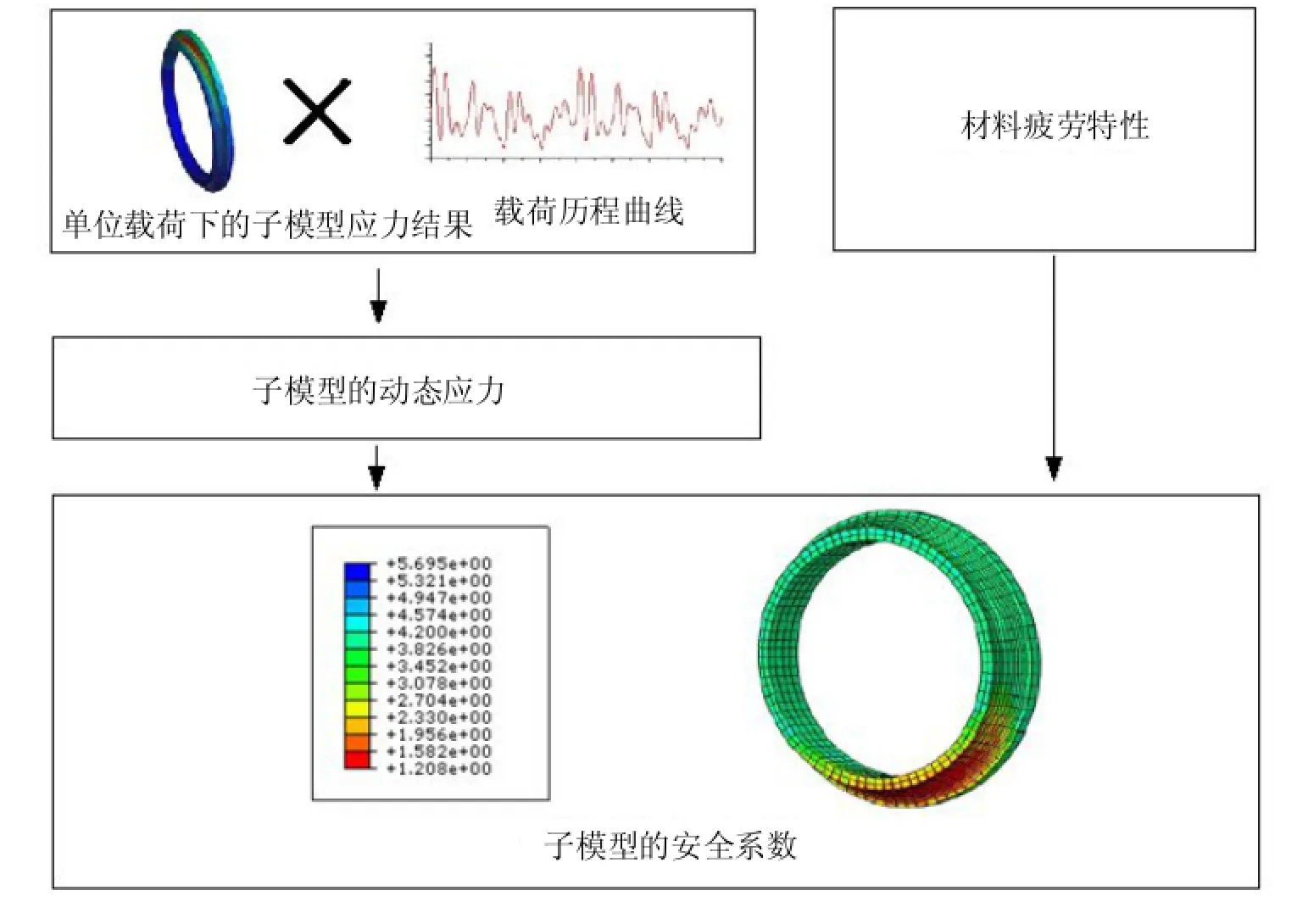
图5 子模型的耐久性分析流程示意图

单位载荷下子模型的应力计算方法已在本文的第2部分作了介绍，而载荷历程可通过试验或多体动力学仿真方法得到[6]。

在考虑到曲轴及相连接部件的柔性耦合作用下，进行曲柄连杆机构与气缸体模型的弹性耦合动力学仿真。曲轴轴系的多体动力学分析是工作状态下的时域仿真计算，包括了动力学载荷计算和弹性体结构的动态响应。建模时要考虑曲轴系的柔性作用，另外系统各部件之间的连接关系通过非线性连接副建立[7]。动力学模型的外部激励包括各缸气体爆发压力和曲轴飞轮端的反向扭矩，是动力学系统的输入。

本文通过多体动力学仿真方法分别得到了图2中第1主轴承中心面、曲柄销中心面、第2主轴承中心面的3个平移自由度和3个旋转自由度，共6个自由度的位移－时间历程曲线。

该曲轴材料为QT900-2，设计寿命为1×107次循环，存活率为99.99%。疲劳分析时考虑应力梯度、表面粗糙度、平均应力、结构尺寸、统计分布等因素对安全系数的影响，根据本企业标准要求，安全系数应大于1.6。

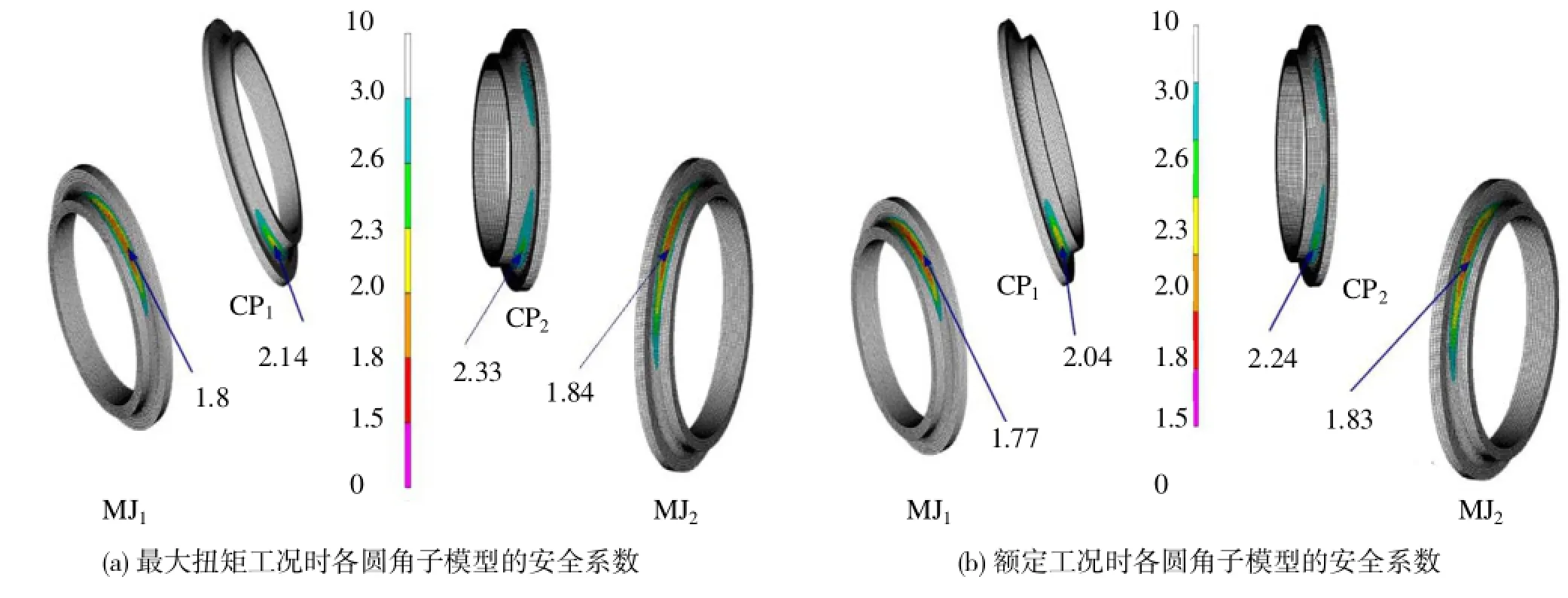
图6 圆角子模型的安全系数云图

4.2 曲轴圆角的疲劳结果分析

根据工程经验，曲轴危险工况一般出现在最大扭矩工况与额定工况，因此本文计算了最大扭矩工况（1 650 r/min）和额定工况（2 200 r/mn）的曲轴圆角安全系数。图6列出了这2个工况下的计算结果。计算结果表明，2 200 r/min时各圆角的安全系数都要小于1 650 r/min时的计算结果，说明额定工况是最危险的工况，而且最小安全系数值为1.77，出现在第1主轴颈圆角处，大于企业的设计要求1.6，满足设计要求。另外，不难发现第2主轴颈圆角和第2曲柄销圆角的安全系数都要分别大于第1主轴颈圆角和第1曲柄销圆角的安全系数，这是因为第2主轴颈的直径大于第1主轴颈的直径，使得曲柄销与主轴颈的重叠度变大，有利于提高安全系数。

5 结束语

（1）将子模型方法引入到曲轴强度及耐久性分析中，与传统方法相比，在满足同等计算精度的前提下，可以显著降低模型规模、提高效率。

（2）文中分析的曲轴最小安全系数为1.77，大于设计标准，满足设计要求，另外增大曲柄销与主轴颈的重叠度可以提高疲劳安全系数。

1万欣，林大渊．内燃机设计[M]．天津：天津大学出版社，1992．

2彭禹．基于虚拟样机技术的发动机子系统设计方法研究[D]．浙江大学，2007．

3丁峻宏，张晓云，李根国．基于高性能计算的曲轴系统动力学与疲劳仿真[J]．农业机械学报．2010，41(9)：218-222．

4石亦平，周玉蓉．ABAQUS有限元分析实例详解[M]．北京：机械工业出版社，2007．

5周传月，郑红霞，罗慧强等．MSC.Fatigue疲劳分析应用于实例[M]．北京：科学出版社，2005．

6 Mourelatos Z P.A Crankshaft System Model for Structural Dynamic Analysis of Internal Combustion Engines[J].Computers and Structures.2001,79(21): 2009-2027.

7陈渊博，郝志勇，张焕宇．基于弯曲疲劳试验的柴油机曲轴疲劳寿命分析及改进[J]．内燃机工程，2011，32(1)：75-78．

Strength and Durability Analysis of Crankshaft Based on Finite Element Sub-model Method

Liu Baolin
（Jiangsu Jianghuai Engine Co.,Ltd.,Jiangsu Yancheng 224001,China）

Aiming at disadvantages such as large degree of freedoms,long time taken while analyzing the strength and durability of crankshaft using conventional method,finite element sub-model method is introduced and investigated for its application.Taking the crankshaft of a single cylinder diesel engine as example,first static analysis under unit load excitation is performed for crankshaft fillets using sub-model method.Afterwards combining static analysis result and displacement-time history data under two load cases(peak torque at 1650 r/min and rated power at 2200 r/min),safety factors for all fillets are analyzed. The entire process and result demonstrate the feasibility and efficiency of the finite element sub-model method for crankshaft strength and durability analysis.

crankshaft,finite element,sub-model,strength,durability

10.3969/j.issn.1671-0614.2011.03.005

来稿日期：2010-05-05

刘保林（1975-），男，工程师，主要研究方向为发动机工作过程和性能优化及有限元分析。