可换环上严格上三角矩阵李代数的拟导子
2011-03-27关琦卞洪亚陈炳凯
关琦,卞洪亚,陈炳凯
(中国矿业大学理学院,江苏徐州 221008)
可换环上严格上三角矩阵李代数的拟导子
关琦,卞洪亚,陈炳凯
(中国矿业大学理学院,江苏徐州 221008)
设R是含幺可换环,Nn(R)表示R上的所有n×n严格上三角矩阵组成的李代数,对Nn(R)上的一个线性变换φ,若存在Nn(R)上的一个线性变换φ¯,对任意的x,y∈Nn(R)都有[φ(x),y]+[x,φ(y)]=φ¯([x,y]),则称φ为Nn(R)上的拟导子.本文定出了Nn(R)上的任一拟导子的具体形式,并对导子的概念进行了推广.
严格上三角矩阵;导子;拟导子;可换环
0 引言
近年来,国内外许多学者研究代数系统上的导子,Jφndrup[1]决定了上三角矩阵环的导子.王登银等[2-3]刻画了可换环上上三角矩阵李代数的导子和一般线性李代数的抛物子代数的导子.偶世坤[4]给出了可换上严格上三角矩阵李代数的导子.Larson[5]将导子的概念加以推广,定义了局部导子的概念.很多学者开始研究局部导子[6,7].最近,Leger和Luks[8]也将导子的概念加以推广,提出了李代数的拟导子的概念.设L为李代数,φ∈Hom(L,L),若存在φ¯∈Hom(L,L),对任意的x,y∈L都有
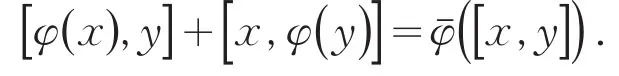
则称φ为L上的拟导子,我们将Tn(R)上所有的线性变换的集合记为gl(L),所有的拟导子的集合记为QDer (L),所有的导子的集合记为QDer(L),所有内导子的集合记为ad(L).因此我们得到以下包含关系:
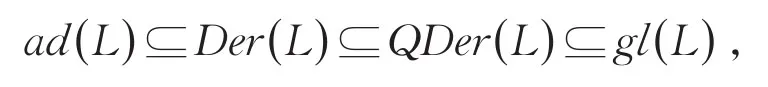
由以上包含关系可知,L上的导子一定为L上的拟导子,可见拟导子是对导子概念的推广.但反过来,L上的拟导子是导子吗?以下的例子给出了否定的答案.
例1纯量变换.设a∈R,考虑映射φ:Nn(R)→Nn(R),x↦x;取φ¯:Nn(R)→Nn(R),x↦2x,则由拟导子的定义易知φ是一个拟导子,但它不是一个导子.
例2设a∈R,考虑映射:

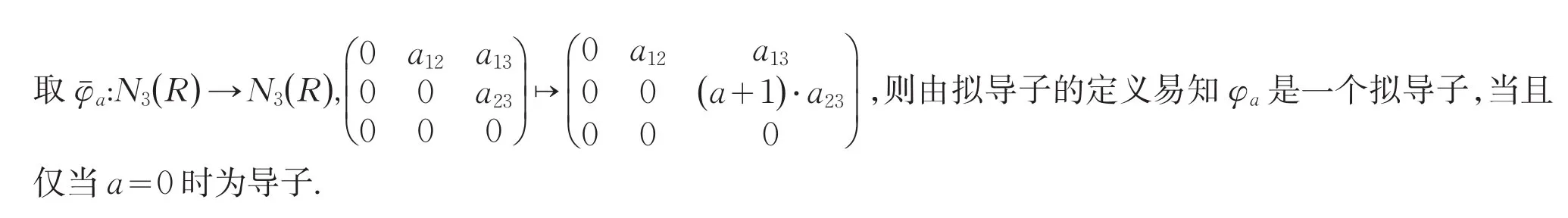
1 Nn(R)的标准拟导子

通过验证这是Nn() R的拟导子,我们称它为可扩的拟导子,当且仅当f=0时λf是导子.
利用上面定义的这些标准的拟导子,我们来刻画Nn() R上的拟导子,下面给出本文的主要定理.
定理1.1设φ是Nn(R)上的线性变换,则φ是Nn(R)上的拟导子,当且仅当

2 引理及定理的证明

考虑⑵式左边第i+1列元可知φ(E1j)第i列元除(1,i)位置外均为0,所以


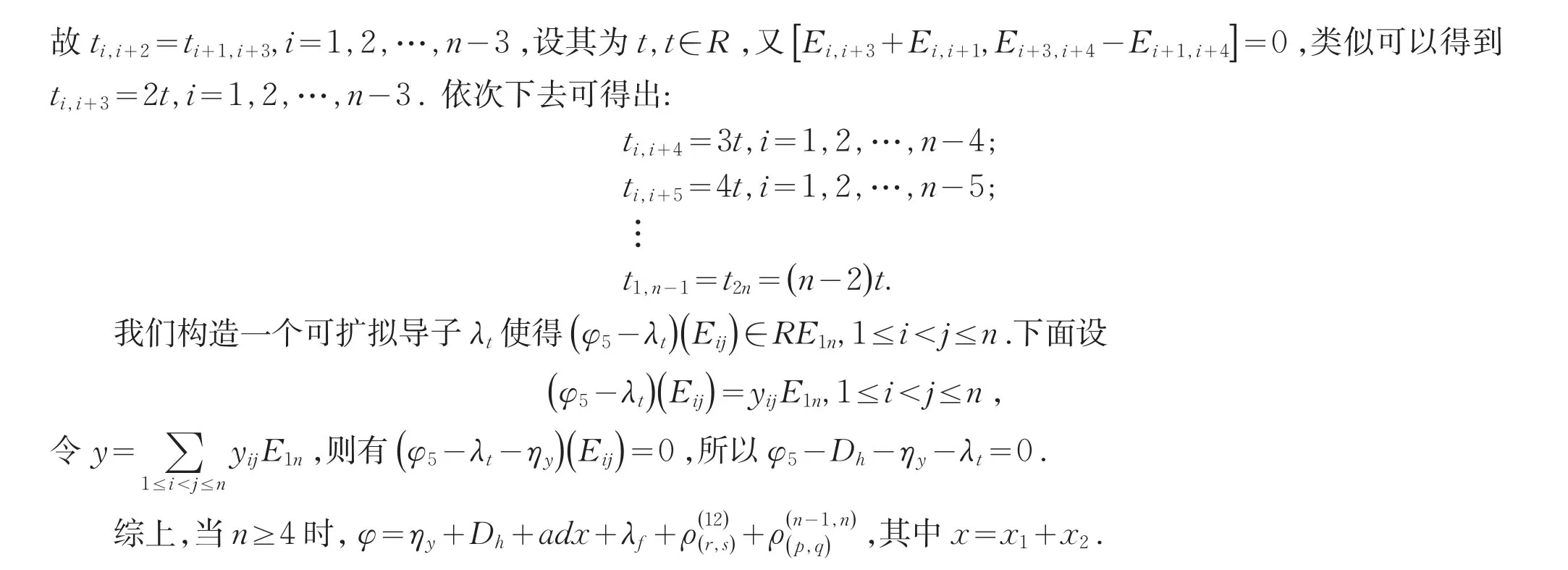
[1]JφndrupS.Automorphisms and derivations of upper triangular matrix ring[J].Linear Algebra Appl,1995,221:205-218.
[2]Wang Dengyin,Yu Qiu,Ou Shikun.Derivations of certain Lie algebras of upper triangular matrices over commutative rings[J]. Journal of Mathematical Research and Exposition,2007,27(3):474-478.
[3]Wang Dengyin,Yu Qiu.Derivations of the parabolic subalgebras of the general linear Lie algebra over commutative ring[J].Linear Algebra Appl,2006,418:763-774.
[4]Ou Shikun,Wang Dengyin,Yao Ruiping.Derivations of the Lie algebra of strictly upper triangular matrices over a commutative ring [J].Linear Algebra App,2007,424:378-383.
[5]Larson D R,Sourour A R.Local derivations and local automophisms of B(H)[J].Proc Sympos Pure Math,1990,51:187-194.
[6]Kadison R.Local derivations[J].J Algebral,1990,130:494-509.
[7]Chrlst R.Local derivations on operator algebras[J].JFunct Anal,1996,135:76-92.
[8]Leger G F,Luks E M.Generalized derivations of Lie algebras[J].J Algebras,2000,228:165-203.
[9]陈清华,王登银,周津名.可换环上严格上三角矩阵李代数上的BZ导子[J].数学杂志,2011,31:55-61.
Quasi-Derivations of the Lie Algebra of Strictly Upper Triangular Matrices over a Commutative Ring
GUAN Qi,BIAN Hong-ya,CHEN Bing-kai
(College of Sciences,China University of Mining and Technology,Xuzhou 221008,China)
LetRbe an arbitrary commutative ring with identity.Denoted byNn(R)the Lie algebra overRconsisting of all strictly upper triangularnbynmatrices.A linear transformationφonNn(R)is called a qusi-derivation of it if there exists a liner transformationφ¯onNn(R)such that[φ(x),y]+[x,φ(y)]=φ¯([x,y])for∀x,y∈Nn(R).In this paper,the authors characterize all quasi-derivations ofNn(R)and generalize the notions of derivations to a more general case.
strictly upper triangular matrices Lie algebra;derivation;quasi-derivation;commutative ring
O152
A
1008-2794(2011)10-0042-06
2011-08-15
关琦(1987—),女,安徽宿州人,中国矿业大学理学院2009级硕士研究生,研究方向:代数及其应用.
