超混沌Chen系统周期映射下的广义同步

汪昭

（常熟理工学院物理与电子工程学院，江苏常熟 215500）

超混沌Chen系统周期映射下的广义同步

汪昭

（常熟理工学院物理与电子工程学院，江苏常熟 215500）

研究了超混沌Chen系统的广义同步化问题.基于Lyapunov稳定性理论，提出了混沌系统在周期性映射下的广义同步方法.用理论和数值计算验证了该方法.最后讨论了各参数对同步的影响.

超混沌系统；广义同步；周期映射

混沌信号的同步是混沌和非线性理论应用于通信工程的核心问题之一.从Pecora和Carroll开创性地提出混沌同步并在电路中实现以来[1]，因为混沌同步运用广泛，受到国内外学者的重视[2].随着研究的深入，同步概念由最初的精确同步（identical synchronization,简称IS）拓展到了广义同步（generalized synchronization,简称GS）[3].文献[4]给出了一类不含平方项混沌系统的精确同步方法.在混沌通信的实际应用中，由于参数失配和各种失真不可避免，同时也出于二次加密的需要，广义同步比精确同步具有更广泛的应用.

广义同步是混沌系统轨道经过二次映射后再进行同步的方法.常规的二次映射有线性映射[5]和非线性映射[6].常见的研究中，映射规则通常不显含时间t.本文以超混沌Chen系统为例，研究了混沌系统的一种特殊含时映射系统，即周期性函数映射下的广义同步方法.

1 广义同步的定义和响应系统的设计

1.1 广义同步定义

定义如下两个非线性系统：

式（1）和式（2）分别为n阶驱动系统和响应系统，式（1）是一个典型的混沌或超混沌系统.其中xi,yi∈R，X=(x1,x2,x3...xn)T，A为n×n维矩阵，φ(x)是非线性向量函数.

现定义一个实数域上的映射zi(t)=H(xi,t)，且H(xi,t)可微.

若当t→∞时，yi(t)=zi(t)，则可认为驱动系统和响应系统达成了广义同步.特殊情况下，若zi(t)=H(xi,t)=xi(t)，为精确同步（IS），所以IS是GS的一种特例.

1.2 超混沌Chen系统的广义同步

超混沌系统是一类具有四维或四维以上的微分系统，且至少有两个或两个以上正Lyapunov指数.2004年，Li等通过设计非线性状态反馈控制器从Chen系统中得到了超混沌系统[7].超混沌Chen系统的微分方程如下：

当参数a=35,b=3,c=12,d=7，并且0≤r≤0.085时，该系统表现为混沌运动，当a=35,b=3, c=12,d=7，且0.085≤r≤0.798时，该系统表现为超混沌运动，当a=35,b=3,c=12,d=7，且0.798≤r≤0.90时系统表现为周期性运动.定义驱动系统和响应系统之间的映射为zi(t)=H(xi,t).

设计一个响应系统Y，满足Y˙=F(y,x,t).令

可证明（4）式可与（3）式达成广义同步.

证明定义广义同步误差系数，用e表示：

显然V≥0，当ki＜0时，显然V·≤0，根据Routh-Hurwitz稳定性理论，此时响应系统可实现混沌同步.证毕.

不失一般性，定义一个周期映射规则：H(xi,t)=xisinωt.由（4）式，响应系统可以写成如下形式：

理论上，该响应系统可以与周期映射后的混沌系统进行同步.下面我们利用数值仿真的方法对该响应系统的有效性进行验证.

2 数值仿真和结果

使用MATLAB的ODE45方法对驱动系统和响应系统进行模拟仿真，以验证响应系统的有效性.为了保证驱动系统处于超混沌状态，我们选取以下参数：a=35,b=3,c=12,d=7，r=0.6；定义k=k1=k2=k3=-3；ω=π，初值：t0=0，驱动系统初值如下：（x1=10,x2=15,x3=30,x4=10），响应系统初值如下：（y1=-10,y2=-14,y3=5,y4=8）.

如图1所示为四条误差曲线，四条误差曲线分别在2s内稳定收敛于0，即超混沌Chen系统（3）与响应系统（9）达到了同步，可见本文设计的广义同步方法是有效的.

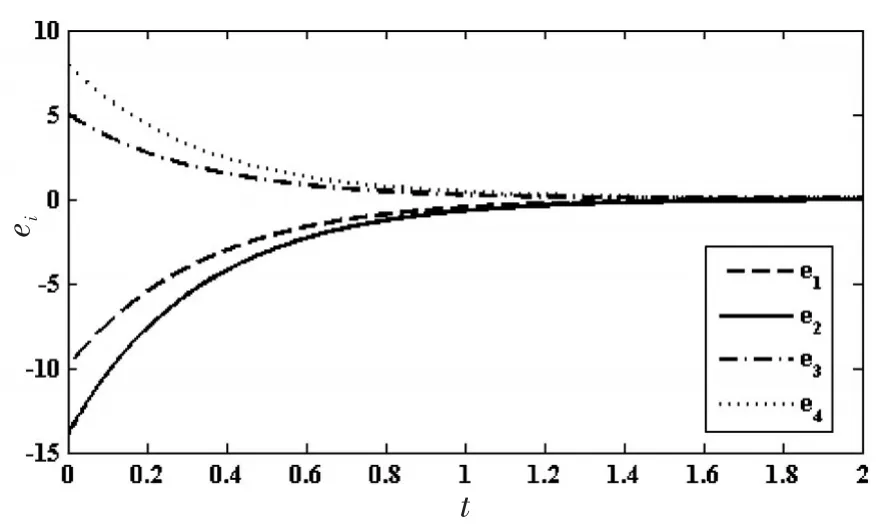
图1 广义同步误差系数随时间变化曲线

3 讨论

广义同步的效率受到驱动系统、映射系统和响应系统各种参量的影响.这些影响主要体现在同步的效率速度和同步稳定性两个方面.Lyapunov函数值的情况是系统同步的主要指标.本文主要利用观察Lyapunov函数值变化的方式，具体分析各参量对同步的作用和影响.

3.1 反馈系数k对同步效率的影响

一般来说，反馈系数k绝对值越大，同步速度越快，保证其他参数不变，观察不同的k值下Lyapunov函数值的变化情况（如图2所示）.

图2所示k分别为-3，-4，-5，-10条件下Lyapunov函数值的变化情况.由图2可以看到，k的绝对值越大，Lyapunov函数收敛越快.所以反馈系数k可以有效调节响应系统的收敛速度.当然，也可以通过分别调整k1,k2,k3,k4的值，以达到单独控制各同步误差曲线的收敛速率的目的.

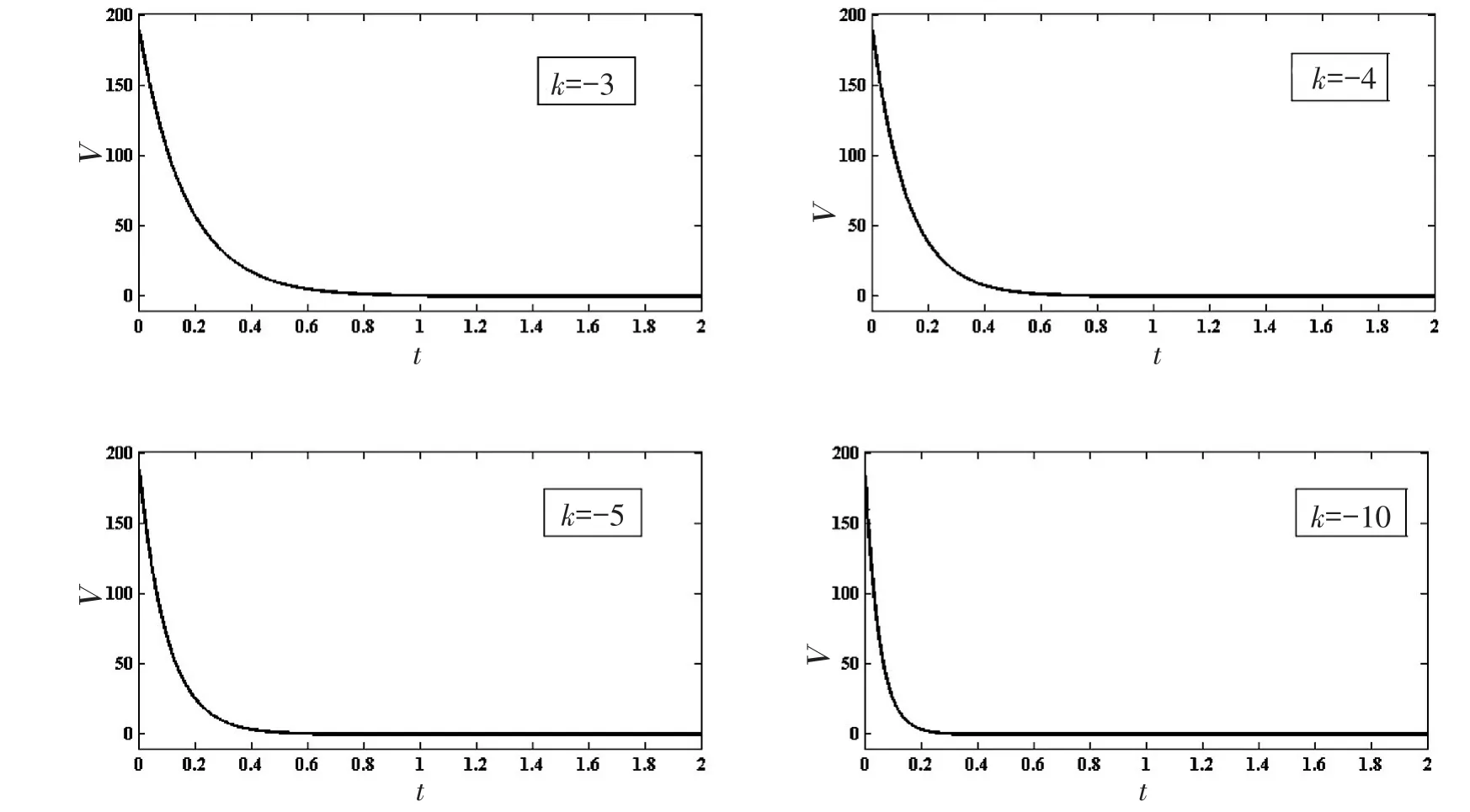
图2 不同k值下Lyapunov函数的收敛情况

3.2 响应系统对驱动系统数据积分采样步长对广义同步的影响

响应系统是一个反馈系统，其动力学性质取决于自身当前状态和驱动系统当前状态的共同作用.数值模拟通常都是离散系统.响应系统（9）的积分过程中必须要对映射驱动系统信号进行采样，得到的数值是一些离散值，并且在下一次采样之前，响应系统积分计算使用的驱动系统信息维持不变.系统积分采样频率大小会影响同步系统的稳定性和计算效率.设采样间隔时间为S，分别在不同的采样时间间隔内研究Lyapunov函数的收敛稳定性，得到的结果如图3所示，时间间隔分别为0.05 s、0.02 s、0.01 s、0.001 s.

参数同上文，k=-3，如图3所示，当s=0.05秒时，Lyapunov函数在收敛与0之后又反复震荡，峰值达到100.函数值在该过程中显得非常不稳定，且具有一定的随机性.这种情况下，同步系统无法满足实际应用的要求；当s=0.02秒时，Lyapunov函数相对稳定，收敛后振荡的峰值在10-20左右，但仍然可以看出明显的波动，当s=0.01秒时，函数曲线收敛后已经基本平直，函数值只是在少数点上出现了幅度较小（小于10）的波动，s=0.001秒时的曲线已经基本平直.由此可见，采样频率越大，广义同步越稳定.但是，并非采样频率越大越好，提高采样频率会造成响应系统的计算量变大，会影响同步的效率.所以，必须根据实际应用要求确定响应系统精度，选择恰当的采样频率，兼顾响应精度和效率.

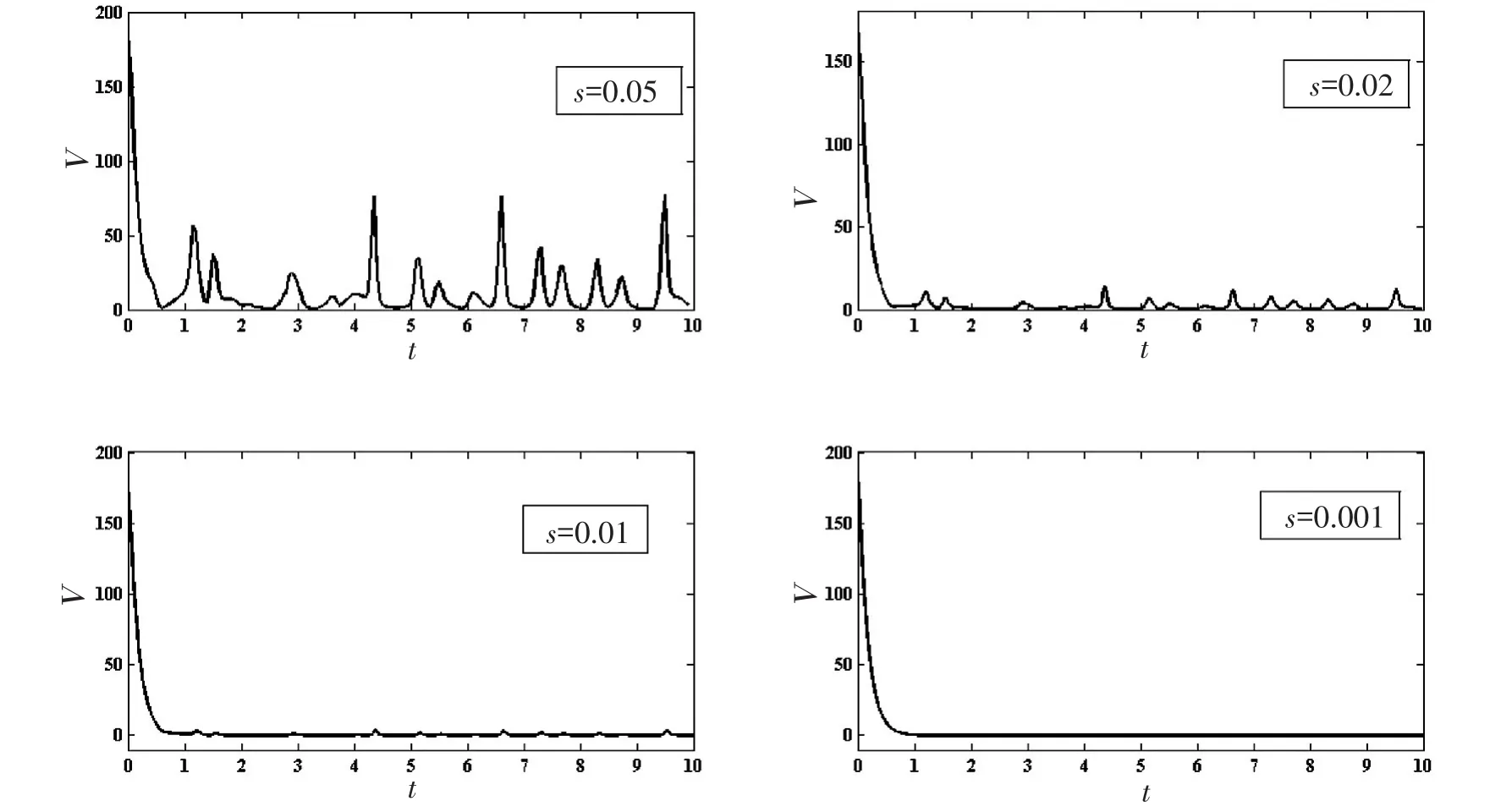
图3 不同采样时间间隔下Lypunov函数的收敛情况.

3.3 映射系统频率对广义同步的影响

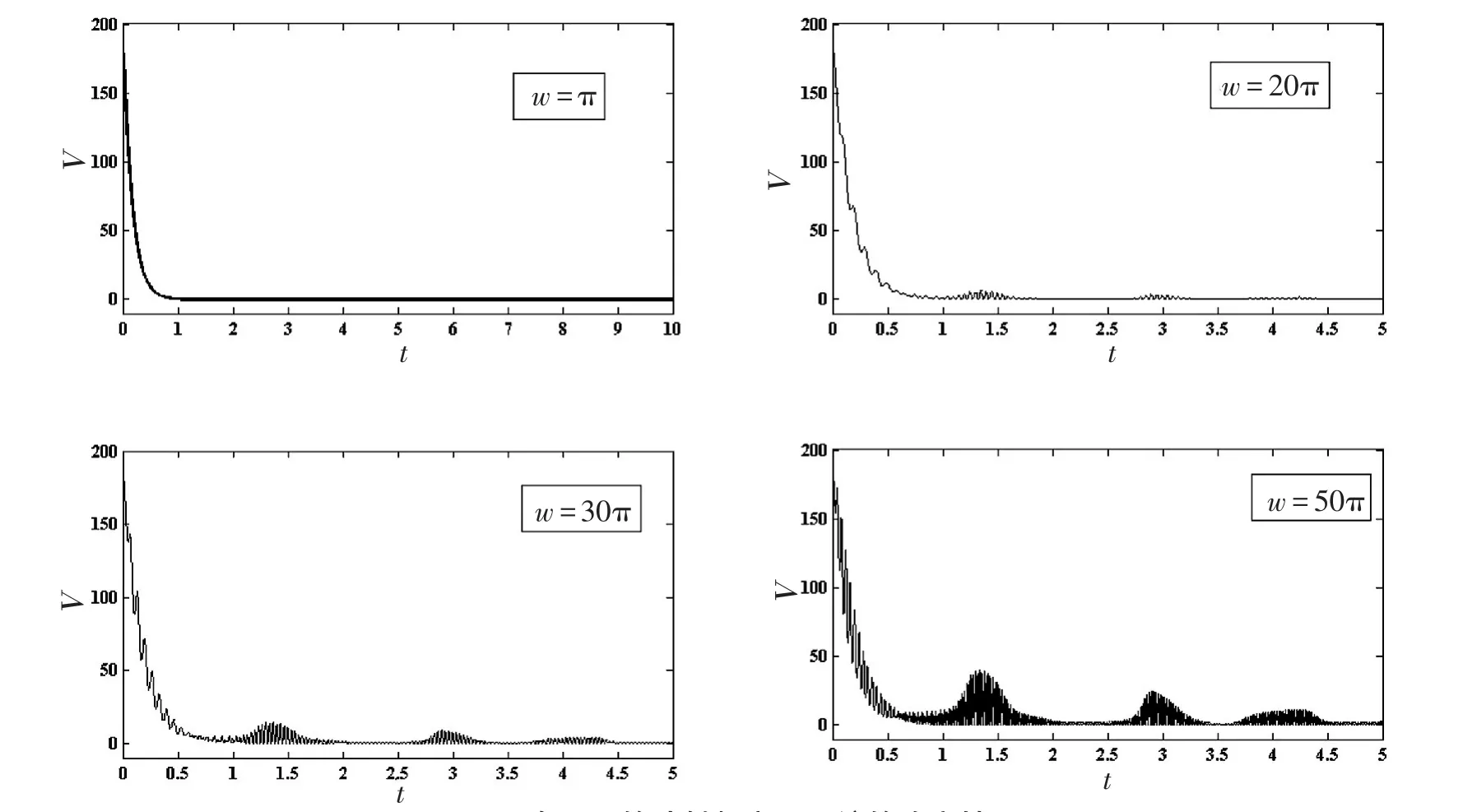
图4 在不同的映射频率下系统的稳定性

综上所述，若发现映射系统频率增加造成广义同步误差偏大时，需要通过减小反馈系统的采样步长来解决上述问题.

4 总结

本文提出了一种在周期映射下，超混沌Chen系统的广义同步问题，并且研究了各参数对同步的影响.含时映射具有一定的普遍性，该方法可以应用到其他的混沌或超混沌系统的广义同步中.

当然，这个问题还有许多方面值得探究和思考：假设驱动系统和响应系统无法实现时间同步，则在响应系统中缺少参数t的情况下，是否可能达成两个系统的广义同步，如可能，该如何做？另外我们观察到在图3和图4中，由采样步长和映射频率改变而造成的Lyapunov函数不稳定起伏曲线图，尽管幅值不同，但位置和相对比例具有一致性，这种相似结构的成因是否与混沌系统自相似结构有关，有待进一步研究.

[1]PECORA L M，CARROL T L.Synchronization in chaos system[J].Phys Rev Lett,1990,64（8）：821-824．

[2]程艳云.混沌同步及其运用[J].南京邮电大学学报（自然科学版），2007，27（3）：80-87.

[3]方锦清.非线性系统中混沌控制方法、同步原理及其应用前景（二）[J].物理学进展，1996,16（2）：174-176.

[4]汪昭.基于线性反馈方法的一类不含平方项混沌系统的同步[J].常熟理工学院学报，2011，25（2）：42-46.

[5]陈明杰，李殿璞，张爱筠.混沌系统的一种广义同步方法[J].哈尔滨工程大学学报，2005，26（1）：59-62.

[6]王小娟，杨志民.Lorenz混沌系统的一种广义同步方法[J].西北师范大学学报（自然科学版），2007，43（5）：47-49.

[7]Li Y X,Tang W K S,Chen G R.Generating hyperchaos via state feedback control[J].Nonliner Dyn,2002,29（1）:3-22.

Generalized Synchronization of Periodic Mapped Hyperchotic Chen System

WANG Zhao

(School of Physics and Electronics Engineering,Changshu Institute of Technology,Changshu 215500,China)

In this paper，the nonlinear generalized synchronization of hyperchaotic Chen system is presented. Based on the Lyapunov stability theory,a new generalized synchronization for chaotic system,which is periodic mapped,is proposed.Theoretical analysis and numerical calculation are provided to show its feasibility.The effect of parameters to the synchronization is also discussed.

hyperchaotic system;generalized synchronization;periodic mapping

O415.5

A

1008-2794（2011）10-0080-05

2011-09-08

常熟理工学院青年教师科研启动基金（KY2009120）资助项目．

汪昭(1982—)，男，江苏常熟人，常熟理工学院物理与电子工程学院实验师，硕士，研究方向：量子混沌，混沌通信．