一种测量谐振系统对地电容的新方法

程玉凯，徐光勇

(1.中国矿业大学信电学院，江苏徐州 221008；2.山东潍坊供电公司，山东潍坊 262500）

一种测量谐振系统对地电容的新方法

程玉凯1，徐光勇2

(1.中国矿业大学信电学院，江苏徐州 221008；2.山东潍坊供电公司，山东潍坊 262500）

介绍了一种测量谐振系统对地电容的新方法，首先向谐振系统中性点注入一定宽度、一定幅值的方波脉冲信号，再测量系统某一电气量（如中性点电压）的振荡频率，求得系统对地电容.本文通过理论分析得出了对地电容的算法，并对方波宽度和幅值做了约束.最后通过计算机仿真分析了阻尼电阻和中性点偏移电压对测量振荡频率的影响，提出了消除影响的措施.

对地电容；谐振系统；方波注入法；仿真分析

0 引言

谐振系统对地电容测量主要有两种方法：被动调感法和信号注入法.被动调感法的原理主要是通过对消弧线圈电感进行调节，观察相应电气量的变化，通过列写方程来求得对地电容，如中性电压极值法、两点法等，由于其调节复杂，测量精度不高，且会改变系统的运行状态，所以现在已经较少使用[1-3].信号注入法的基本原理是向中性点或者母线PT二次侧注入一个电流信号，通过测量注入信号两端电压变化，求得电容电流，由于其对系统几乎不造成影响，测量精度相对较高，因此得到了广泛应用.信号注入法又可分为两类，一类是扫频法，一类是分频法[2，4，5].它们各有优缺点：扫频法是通过改变注入的可调频电流信号的频率使系统在某一频率达到谐振，利用谐振时的等值关系，求得对地电容，这种方法测量简单，精度较高，但为了减小误差，需要选择的扫频步长尽可能小，因此测量时间较长，实时性不好；变频法是向中性点或者母线PT二次侧注入一个或者两个特殊频率（一般不能为工频的整数倍）的电流信号，通过测量信号两端的电压矢量参数，列写方程，求得对地电容，这个方法虽然操作简单，测量安全，但一个很大的缺点是选择注入信号频率的复杂性：若是选择过高，则求得系统的容抗过小，会使得电容测量值远远偏离实际值，若是选择频率过低，消弧线圈和PT励磁阻抗分流作用增强，使测得的接地电容的值产生很大的误差.

本文介绍的方波脉冲注入法，是在这两种信号注入法的基础上提出的，因为不同频率的正弦信号叠加可以等效为一定宽度的脉冲方波信号，于是当向系统注入一定宽度的方波脉冲信号时，会使得谐振系统发生并联振荡，只要检测出这个振荡的频率，经过一定的算法就可以求出系统的对地电容.

1 方波脉冲注入法测量对地电容的理论分析

1.1 对地电容测量的等值电路

系统对地电容测量的等值电路如图1所示.

2 方波脉冲宽度和幅值的选择

方波脉冲信号并不是随便选取的，若选择注入信号能量过大，它会对电力系统产生影响，对配电网的安全运行不利；若选择信号能量过小，则会对系统接地电容的测量值造成较大的误差，因此必须对注入的方波脉冲的能量进行约束[6，7].方波脉冲能量的主要体现是其脉冲宽度和幅值.

2.1 对方波脉冲宽度约束

电路在T时刻，注入信号两端的电压Uin(T-)可表示为：

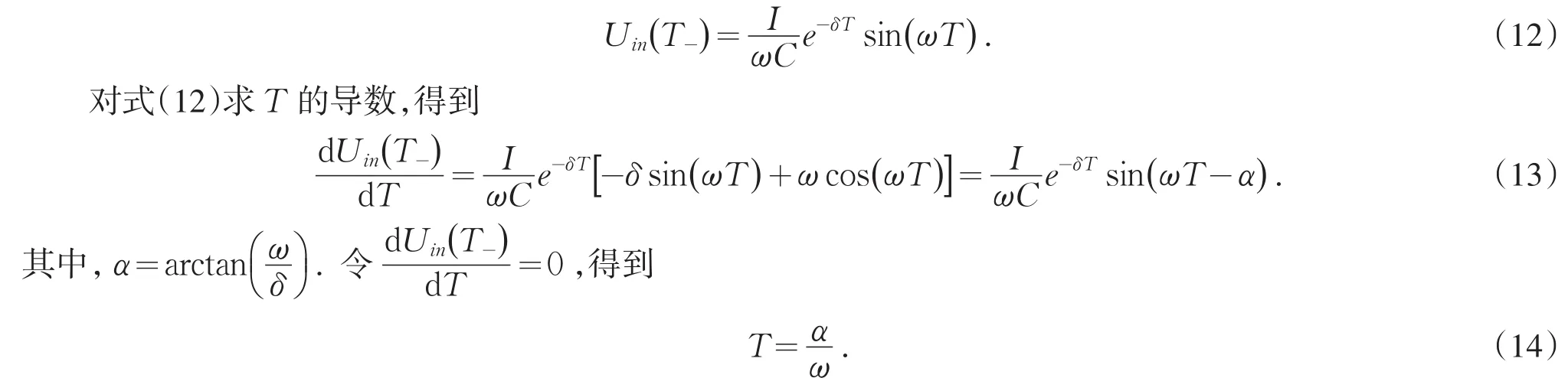
2.2 方波脉冲幅值的选择

规程规定，配电网中性点电压不能大于系统相电压的15%，所以当注入中性点的脉冲幅值选择过大时，会对系统产生不利影响，因此必须对其进行限制[7-10].由式（9）可知，当中性点位移电压不存在或者很小时，必须满足

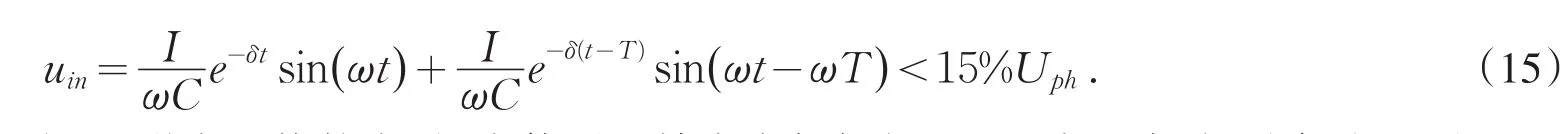
另外，当幅值选择过小，且噪音干扰较大时，会使测量精度大打折扣.经过大量实验，我们发现对于10 kV系统来说，方波脉冲的幅值应该选择在50～300 V.

3 计算机仿真验证

本文选择Matlab/Simulink进行仿真分析，具体设置参数为：10 kV系统，预设三相对地电容之和为25.8 μF，设置消弧线圈电感为5.95 H.注入的方波脉冲信号幅值为70 V，脉冲宽度为30 ms.

本文的仿真主要是分析验证中性点偏移电压和阻尼电阻对系统振荡频率测量的影响.首先分析当中性点偏移电压较小（这里设置为0）时的情况.下面两图中，上面的图为未投入阻尼电阻时中性点电压波形图，下图为当设置阻尼率10%时中性点电压的波形图.

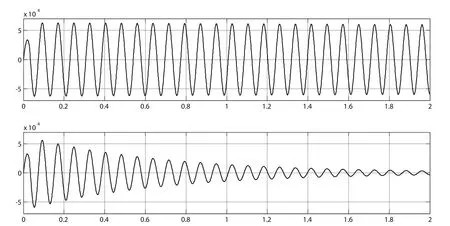
图2 有阻尼和10%阻尼时中性电电压波形（上图为无阻尼投入，下图为有阻尼投入）

由图2可以看出，当未投入阻尼时（理想状态下），系统状态为等幅振荡，对频率测量只需要检测过零点处时刻，即可得到所要测量的频率；当投入阻尼时，由于其消耗方波脉冲的能量，导致波形呈现衰减振荡，对其进行过零时刻检测时，发现得到的测量频率结果与未为投入阻尼时相同，这说明阻尼的投入，只是使系统发生衰减振荡，不会对振荡频率造成影响.

下面再看当中性点存在较大偏移电压时（系统对地总电容不变），不投入阻尼和投入阻尼的情况，如图3所示.

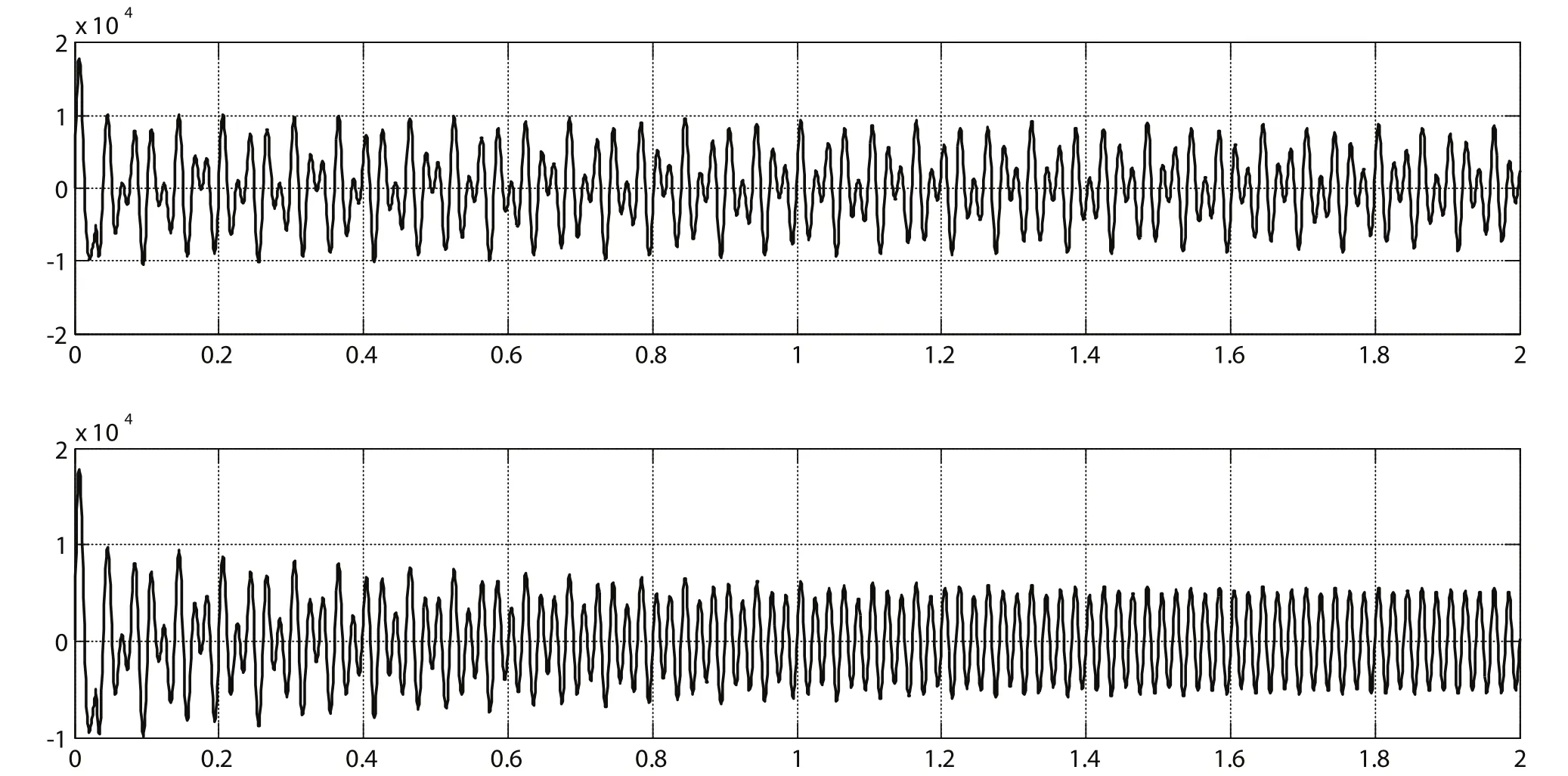
图3 中性点偏移电压较大时注入信号两端的电压波形（上图为无阻尼投入，下图为有阻尼投入）

由图3可知，当系统中性点偏移电压较大且无阻尼时，中性点电压产生严重的畸变，这主要是由于振荡信号与工频信号叠加产生的结果，因此很难测量系统的振荡频率；当投入阻尼时，中性点电压也产生了畸变（特别是在0～0.7 s），0.7 s以后波形趋于稳定，这是由于阻尼在0.7 s以后使得信号衰减到对工频信号影响很小的地步，因此，0.7 s以后出现的波形频率为工频，这样也是无法测量振荡频率的，必须采取一定的措施滤除工频信号的干扰.

将未注入方波脉冲时中性点电压作为对比量，采用自适应滤波算法对得到的信号滤波（滤波中性点偏移电压干扰），可以得到图4的波形.

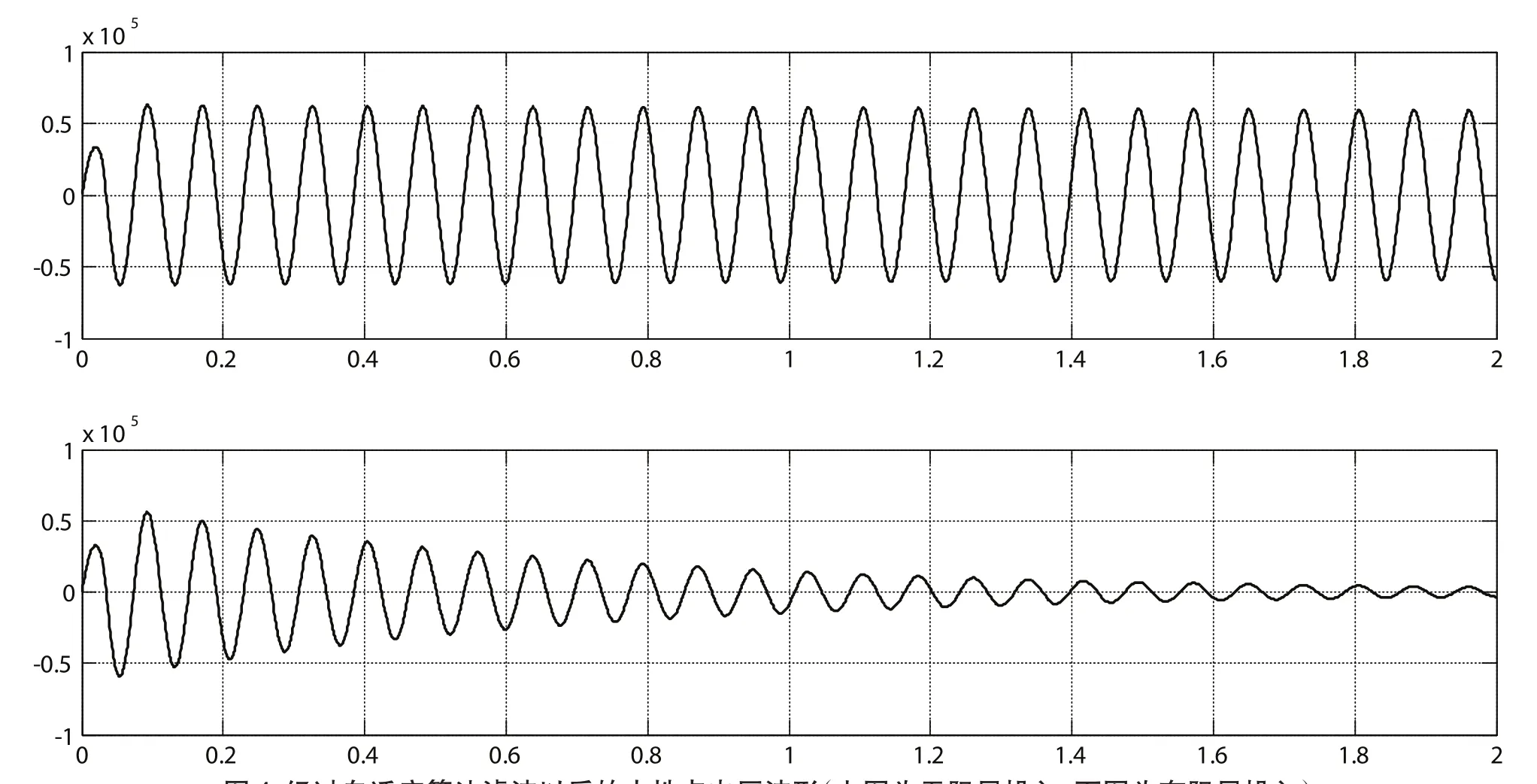
图4 经过自适应算法滤波以后的中性点电压波形（上图为无阻尼投入，下图为有阻尼投入）

从图4可以很容易地检测出我们所需要的频率，根据图2和图4所示的波形，测得连续三个过零点之间的间隔为0.769 s，即系统的振荡周期为0.769 s，于是振荡频率f=13 Hz，然后根据式（11）得到我们所求的C=25.22 μF，预设值C=25.8 μF，误差率为2.24%.

根据本方法改变系统对地电容值重复测量，得到的测量值与理论值之间的误差率如表1所示.

其中理论值为在Matalab/Simulink环境下搭建模型中对地电容设定值，测量值为根据本方法得到的对地电容数据.

由表1可以看出本方法测量系统接地电容误差率较小，精度较高.

表1 测量值与标准值的误差率

4 结论

本文介绍了一种新的电容电流测量方法，它通过向电网注入方波脉冲信号，测量系统振荡频率的方法，求得对地电容值.通过理论分析和计算机仿真，可以看出本方法操作安全，计算简单，测量精度较高，因此实用性较强.

[1]易文韬，李甦康.配电网电容电流测量方法探讨[J].江西电力，2010（1）:13-17.

[2]王崇林.中性点接地方式与消弧线圈[M].徐州：中国矿业大学出版社，1999：1-111.

[3]马强.配电网谐振接地系统若干问题的研究[D].保定：华北电力大学，2006.

[4]Caixu A.new arc-suppression coil with magnetic bias and its characteristics analysis[C].Electrical Machines and Systems，Sixth International Conference，2003，2:903-906.

[5]连鸿波，裴善鹏，曲轶龙，等.谐振接地电网的电容电流自动跟踪测量[J].郑州工业大学学报（工学版），2005，26（2）：51-54.

[6]Lian Hongbo，Yang Yihan，Zhu Xukai.Research on the compensation Mode and New Principal-auxiliary Arc-suppression Coil in the Resonant Ground System Power System Technology[J].International Conference on Volume,2004（1）:723-728.

[7]阿吉古丽·买买提.小电流接地系统的接地电容电流的测量[J].新疆电力技术，2008（1）：24-26.

[8]冉启鹏，陈欣，代正元，等.10kV配网系统电容电流的测算[J].云南电力技术，2010（6）：46-49.

[9]任忠库，孙亮，刘颖.系统电容电流测试及消弧线圈调整[J].黑龙江电力，2009（6）：457-459.

[10]曾祥君，刘张磊，马洪江，等.配电网电容电流实时测量技术[J].电力系统自动化，2008（3）：61-65.

A New Method of Measuring Ground Capacitor in Resonant System

CHENG Yu-kai1,XU Guang-yong2

(1.School of Information and Electrical Engineering,China University of Mining and Technology,Xuzhou 221008,China; 2.Power Supply Company of Weifang,Weifang 262500,China)

A new method of measuring the ground capacitor of resonant system is introduced.by injecting a certain width and amplitude square wave pulse signal into neutral point,then measuring the amount of an electrical system(such as the neutral point voltage)of the oscillation frequency,and finally using a certain algorithms,system-to-ground capacitance is obtained.In this paper,the theory of this method is analyzed;thus capacitance of the algorithm is obtained,and the width and amplitude of each wave are restricted.Finally,through computer simulation,the impact of the damping resistors and neutral point voltage offset on the oscillation frequency measurements is discussed,and the method of eliminating the impact of proposed measures is put forward and the simulation results prove the theory analyzed.

ground capacitance;resonant system;method of square wave injection;simulation analysis

TM835.4

A

1008-2794（2011）10-0085-06

2011-09-11

程玉凯（1987—），男，山东潍坊人，中国矿业大学信电学院硕士研究生，研究方向：供电安全及智能电器.