基于双树复小波变换与非线性扩散的图像去噪
2011-03-27王宏志
武 伟, 王宏志
(长春工业大学计算机科学与工程学院,吉林长春 130012)
0 引 言
基于偏微分方程的图像处理是近年来研究的一个热点[1-6],其来源于物理学中的热传导,结合变分方法、泛函分析、微分几何等数学工具,建立和偏微分方程相关的模型,使其在图像分割、图像平滑、图像识别等图像处理领域得到了广泛的应用。其中非线性扩散方程是图像去噪领域中应用最为广泛的模型,由Perona和Malik[4]于1990年提出,该非线性扩散模型根据图像梯度对图像进行不同程度的平滑滤波,具有各向异性。随着研究的深入,人们发现经典P-M方法虽然在特征保持方面成果显著,但从数学模型的观点看,其模型却存在一定缺陷,由于扩散函数是基于图像梯度计算出来的,从而对噪声很敏感,一旦噪声强度加大,在滤除噪声的同时,对图像的视觉破坏也相当严重。因此,人们对P-M模型进行了大量的改进。
文献[7]得到正则化后的P-M扩散方程; Whitaker和 Pizer[8],Weickert[9]以及 Carmona[10]等改进了P-M 扩散模型;2000年,Chen[11]等得到了较好的非线性扩散模型。在同样的理论框架下,Osher与 Rudin[12-13]关于冲击滤波器(Shock Filter)和Rudin,Osher,Fatemi[14]关于全变差去噪的研究工作显示了理解偏微分方程在图像处理中应用的必要性与重要性。
双树复小波变换是为克服通常的离散小波变换的缺陷而提出的。当对应小波基(近似)满足Hilbert变换关系时,双树复小波变换能够极大地减小通常的实小波变换中的平移敏感性,改善方向选择性。这些优点使双树复小波变换在图像去噪领域得到了广泛的应用。
1 双树复小波变换
传统的离散小波变换存在平移敏感性和缺乏方向选择性等缺点,为了克服这些缺点,Kingsbury[15-16]等提出了双树复小波变换(DT CWT)。双树复小波变换采用了二叉树架构的两路DWT,一树生成变换的实部,一树生成虚部,如图1所示。

图1 双树复小波变换
Kingsbury的思路是:对于第一层分解,如果两树滤波器之间的延迟恰是一个采样间隔,那么就可以确保b树中第一层的二抽取正好采样到a树中因二抽取所丢掉的采样值(这样就等价于没进行二抽取,而且非常易于实现,如在b树前加一个采样周期延迟即可);对于以后的各层分解,为了保证两树在该层和所有前层上产生的延迟差的总和相对于原始输入为一个采样周期,两树对应滤波器的相频响应之间应有半个采样周期的群延迟,且两滤波器的幅频响应相等。为了保证线性相位而采用双正交小波变换,Kingsbury要求一树的滤波器为奇数长,另一树的滤波器为偶数长。如果在每树的不同层次间交替采用奇偶滤波器,那么这两树就会呈现好的对称性。
2 非线性扩散方程
Perona和Malik[4]提出了一种非线性扩散方程,该方程通过时间变化的更新(即迭代)使得图像逐渐平滑,从而达到去除噪声的目的。其数学表达式为:

式中:

其中,▽u是图像的梯度,定义为:

div(v)为散度,定义为:

一般情况下,扩散函数c是图像的梯度函数,随着梯度的增加而单调下降,见式(2)。该扩散系数决定了扩散进行的方式,提供了一种局部自适应的扩散控制策略,使得扩散尽可能在噪声的位置进行,而在图像的边缘位置停止。
P-M方程的离散形式为:

这样P-M方程作用于图像的模板为:

这里像素s的权值不再是个固定值,而是跟像素s的空间位置有关,如果像素位于梯度大的位置,由于c(x,y,t)是以|▽u(x,y,t)|为变量的单调下降函数,所以其相应的权值就会小,平滑力度就弱;反之,如果像素位于梯度小的位置,其平滑力度就强。而图像的边缘通常是梯度较大的,而其它区域梯度较小,所以,P-M方程能在保留甚至加强边缘的情况下实现对图像噪声的去除。
3 双树复小波变换与非线性扩散结合去噪
1999年,Kingsbury[15]提出了DT-CWT变换,它具有以下特点:近似平移不变性,良好方向选择性,有限数据冗余,高效计算效率,较好重构效果等。DT-CWT变换可以通过2棵离散小波树(Tree a,Tree b)并行实现实部和虚部运算(见图1)。2棵树分别作用于图像的行和列,产生双树结构。每级分解后得到2个低频带(低频部分用于产生下一尺度上的低频与高频部分),同时得到6个方向(±15°,±45°,±75°)的高频子带,可以更好地描述纹理和边缘等细节特征。
利用双树复小波在纹理和边缘等细节处理的优点,结合非线性扩散滤波提出了一种新的图像去噪方法。首先对噪声图像进行双树复小波分解,生成6个方向的高频子带图像,然后针对这些子带图像复小波系数矩阵的不同特点进行非线性扩散。最后进行双树复小波逆变换,得到最终滤波后的图像。
算法的主要步骤如下:
步骤1:对图像进行一次双树复小波变换。设二维图像 u(x,y)分解后的低频子带图像为AL1,AL2;高频子带图像分别为WH1,WH2,WH3,WH4,WH5,WH6。
步骤2:将得到的高频子带图像分别进行非线性扩散滤波。
步骤3:用非线性扩散滤波处理后的高频子带图像进行双树复小波逆变换重构原图像。
4 实验分析
实验选取256×256的灰度图像作为仿真图像,以PSNR(peak signal-to noise ration)来评价图像质量。加入均值为0,方差为σ的高斯噪声,分别采用双树复小波、非线性扩散、文中方法进行去噪,得到的图像如图2所示。



图2 三种方法去噪后的图像
阈值参数取0.05,非线性扩散的时间空间步长分别为t=0,h=1,迭代次数50,这里阈值参数是根据多次实验结果选取的最佳值,为了体现算法的有效性,同时尽量降低计算复杂度,所以迭代次数为50,实验结果见表1。
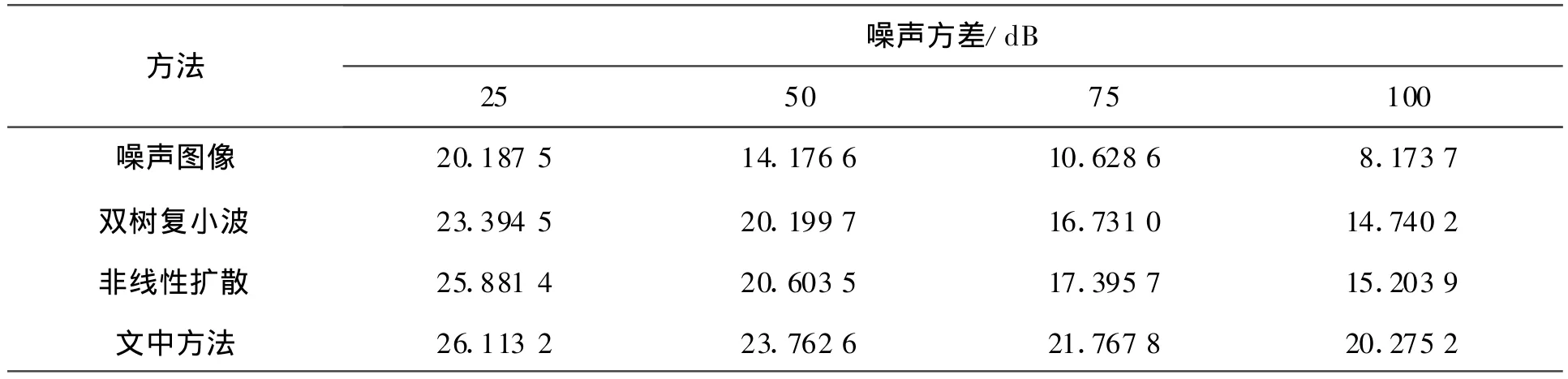
表1 采用三种去噪方法的PSNR比较
5 结 语
利用双树复小波与非线性扩散的优点,将两者结合提出了一种混合去噪方法。通过实验分析,该方法优于传统的双树复小波和非线性扩散法,能更好地去除噪声并保留图像的边缘和细节等信息。实验验证了算法的有效性。
[1] Rudin L,Osher S,Fatemi E.Nonlinear total variation based noise removal algorithms[J].Phys D,1992,60(1/4):259-268.
[2] M razek P,Weickert J,Steidl G.Correspondences between wavelet shrinkage and nonlinear diffusion [A].Scale Space Methods in Computer Vision[C]. Berlin:Springer Press,2003:101-116.
[3] Rudin L,Osher S.Total variation based image restoration with free local constraints[A].Proceedings of the IEEE International Conference On Image Processing[C].Piscataway:IEEE Press,1994:31-35.
[4] Perona P,Malik J.Scale-space and edge detection using anisotropic diffusion[J].IEEE T rans on Pattern Analysis and Machine Intelligence,1990,12(7):629-639.
[5] Qu Tianshu,Dai Yi-song,Wang Shu-xun,et al. Adaptive wavelet thresholdingdenoisingmethod based on SURE estimation[J].Electronic Journal.,2002,30(2):266-268.
[6] Yuan Zejian,Zhang Nan-ning,Zhang Yuan-lin,et al.A design method for nonlinear diffusion filter and its application[J].Chinese J.Computers,2002,25(10):1072-1076.
[7] Scherzer O,Weickert J.Relations between regularization and diffusion filtering[J].J.M ath.Image Vision.,2000,12(1):43-63.
[8] Whitaker R T,Pizer S M.A multi-scale approach to non-uniform diffusion[J].CVIGP;Image Understanding,1993,57(1):99-110.
[9] Weickert J.Multiscale texture enhancement Computer analysis of images and patterns[J].Lecture Notes in Computer Science,1995,970:230-237.
[10] Carmona R A,Zhong S F.Adaptive smoothing respecting feature directions[J].IEEE Transactions on Image Processing,1998,7(3):353-358.
[11] Chen Y,Vemuri B,Wang L.Image denoising and segmentation via nonlinear diffusion[J].Computer and Mathematics with Applications,2000,39(5/6):131-149.
[12] Osher S,Sethian J A.Fronts propagating with curvature-dependent speed;Algorithms based on Hamilton-Jacobiformulations[J].Journalof Computational Physics,1988,79(1):12-49.
[13] Osher S,Rudin L I.Feature-oriented image enhancement using shock filters[J].SIAM Journal of Numerical Analysis,1990,27(4):919-940.
[14] Rudin L I,Osher S,Fatemi E.Nonlinear total variation based noise removal algorithms[J]. Physica D.,1992,60:259-268.
[15] Kingsbury N G.Complex wavelets for shift invariant analysis and filtering of signals[J].Appl. Comp.Harmonic Anal.,2000,10(3):234-253.
[16] Kingsbury N G.The dual-tree complex wavelet transform:A new efficient tool for image restoration and enhancement[A].Proc.European Signal Processing Conf[C].[S.l.]:Rhodes,1998:319-322.
