曲轴的参数化有限元分析
2011-07-09田忠静王金辉李海梅
田忠静, 王金辉, 李海梅
(吉林省通化市农机研究设计院,吉林通化 134000)
0 引 言
曲轴是压力机传递运动和动力的重要零件,具有结构复杂、加工制造困难、承受载荷较大并且受力状态复杂等特点[1],其结构如图1所示。
曲轴的结构参数不仅影响着整机的尺寸和重量,而且在很大程度上影响着曲柄压力机的可靠性与寿命。

图1 曲轴结构图
曲轴在每次冲压时都要往复运动一周,应力对其影响相当大,而在如此频繁的应力作用下,曲轴的主要失效形式为疲劳断裂[2],所以有必要对其上的关键点进行分析,以便找到薄弱的易损坏点。找到容易损坏的地方后,就可以采取相应的措施进行防护或改进设计。但这一切的前提条件是要找到受应力破坏最大的地方。传统的校核方法对曲轴的断裂失效分析主要集中在静态极限强度理论[3],而日益发展的科学技术对曲柄压力机要求日趋严苛,这就需要对其更进一步分析,所以利用有限元分析软件对其进行动态分析非常必要。
1 有限元数学模型的建立
有限元法是将实体对象分割成不同大小、种类、小区域,称为有限元。根据不同领域的需求推导出每一个元素的作用力方程,组合整个系统的元素并构成系统方程组,最后将系统方程组求解[4]。
由于该曲轴零件是一个对称的模型,利用对称性原理,可以只分析一半,以此来代表整个零件的受力结果[5]。
曲轴的材质为45#钢,采用弹性模量和泊松比来描述材料的性能,设弹性模量为2e+5 MPa,泊松比为0.25。
在曲轴的两个轴径处添加轴承载荷,大小为50 000 N,方向相反[6]。
在对称面上添加约束:X,Y,Z方向的平移位移为0;在Y轴上取两点,靠下的点X,Y方向的旋转量为0;靠上的点Y方向的平移位移为0[6]。
选择“十节点四面体单元”,将全局单元尺寸大小选择20,划分网格,其结果如图2所示。

图2 曲轴的计算模型
用控制变量的方法运行计算,分析曲轴不同参数组合的最大拉应力和最大剪应力,记录结果。
曲轴分析模型示意图如图3所示。

图3 曲轴分析模型示意图
曲轴尺寸见表1。
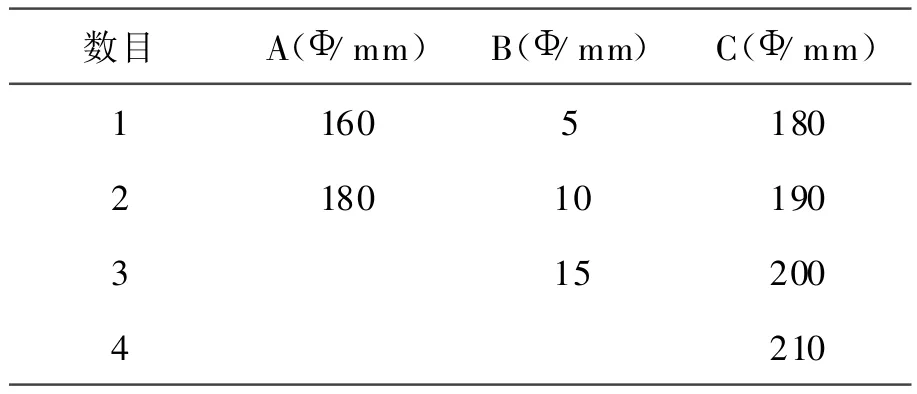
表1 曲轴尺寸表
由图3可知,按照表1改变各处数值,分析A,B,C这3处在不同尺寸情况下的拉应力和剪应力,其结果见表2。
2 数据分析
表2中所列出的数据是该曲轴处于不同参数组合时应力的变化规律,以最大拉应力为研究对象,将所有数据组合曲线化,如图4所示。

图4 曲轴各处数据组合的应力曲线图
分析可见,第一组数据极具代表性,若以其作为分析典型,分析结果可能会较好、较稳定,其数据见表3。
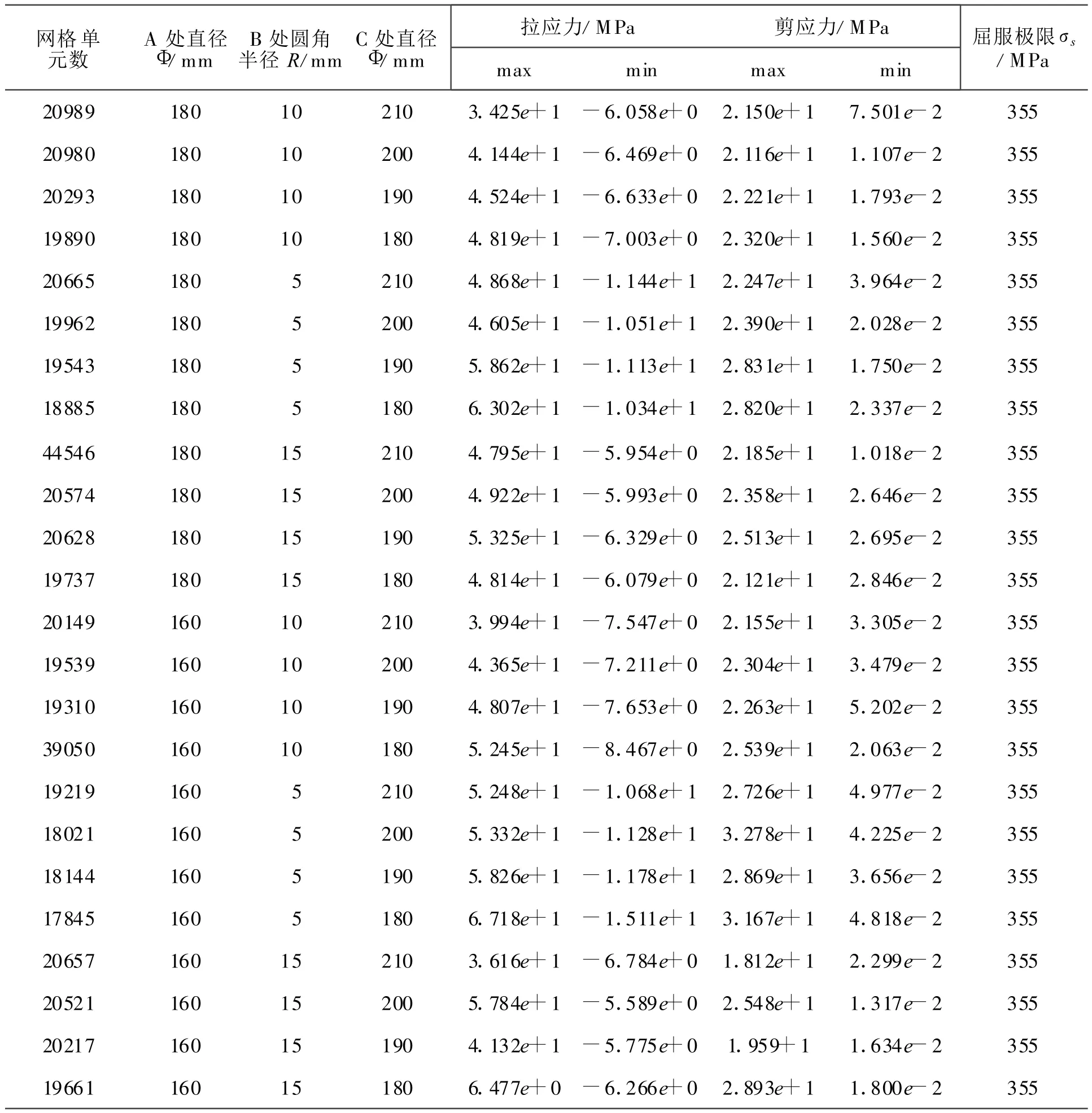
表2 曲轴应力值

表3 第1组数据组合下的应力值表
利用ANSYS分析软件,查看表3中4种尺寸数据组合的曲轴应力分布图如图5所示。
由以上的4组应力分布图可见,它们大同小异,都是在B处出现了最大的拉应力,但其属于应力集中,屈服后其屈服范围向周围扩展会导致应力分散,并不会对曲轴构成威胁。除了B处以外,C处表面上的颜色对应色谱上的值也很大,同时,C处工作时所受的作用力是一个循环应力,其对C处的破坏力要比圆角B处大得多,因此,C处圆柱面的下方是最危险的,故应对其进行深入分析。
由于该曲轴的材料为45#钢,而45#钢是一种塑性材料,对于塑性材料来说,拉应力对其破坏力较大,所以应对最大拉应力作深入分析,忽略剪应力的影响。
由图4可见,最大拉应力的数值分布近似于一条直线,因此设直线y=a1+a2x,用最小二乘法来求直线方程。
设变量J代表了4个应力值的点与直线距离之平方和:
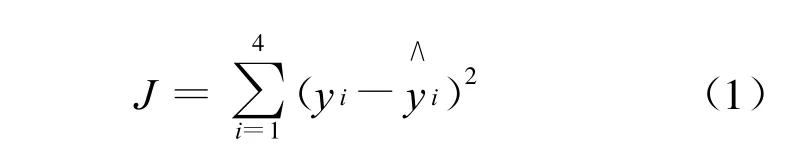
式中:yi实际应力值点的数值;
根据所设的直线方程

将其代入式(1),得:
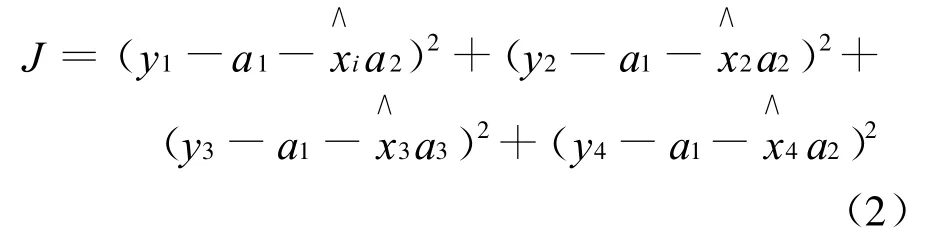
当J最小时,4个点才最靠近直线,也就是说,这时直线最接近理想状况。要使J最小,则要满足

由式(3)可得
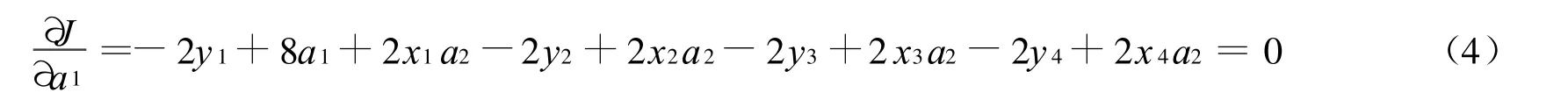

由式(4)和式(5)可得:

可将式(6)写成线性齐次矩阵方程形式:

其中
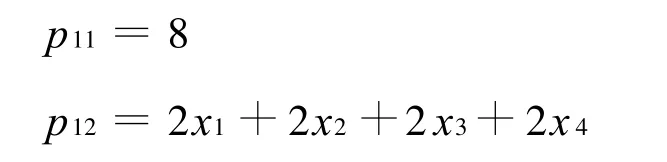

两边同乘以一个逆矩阵得:

代入实际数据,从而解得:

所以直线方程为:
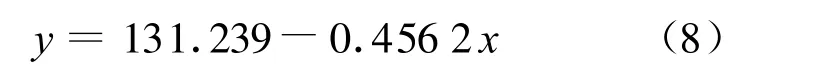
在实际中,横坐标x代表C处的直径d,纵坐标y代表最大拉应力σmax,所以在实际中可将此直线方程形式写成:
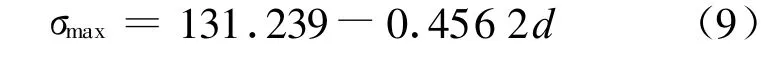
其方程曲线如图6所示。

图6 曲轴最大拉应力随C处直径变化的方程曲线图
3 结 语
在经过数据分析之后,结论如下:
1)最危险处在C处圆柱面的下方。
虽然在圆角处有着最大的应力,属应力集中,但是屈服后,其屈服范围向周围扩展导致应力分散,并不会对曲轴构成威胁。而C处的应力数值虽然不是最大,但从数值上来讲也已经在应力色谱中达到了中等偏大的级别。而且在工作环境中要考虑到,C处在工作时所受的作用力是一个循环应力,因此,该循环应力对C处圆柱所产生的破坏力要比圆角处大,所以在C处圆柱面的下侧是最危险的。
2)以C处的直径变化为未知数的曲轴最大拉应力方程为:

C处直径越大,则应力越小,抗应力破坏能力越强。
由图6可见,当C处直径在180~210 mm之间从小变大时,该处的最大拉应力随之由大变小,这意味着当C处直径越大,该处的抗破坏能力越强,曲轴越安全。
3)该方程仅在C处直径在180~210 mm之间变化时,确保有效。
因为在数据分析时,C处直径是在180~210 mm之间取4个值进行分析,而且后面的公式总结也是基于C处直径在180~210 mm之间所做出的,所以,这个经验公式只能确保在此区间内有效。
4)经计算,经验公式误差很小,可以认为是准确的。
由图6可见,经验公式的直线与实际数值的偏差,误差范围基本在2.08%~3.33%之内,全都小于5%,所以,当C处直径在180~210 mm之间变化时,经验公式是基本有效的。
综上所述,当A处、B处的尺寸保持不变,仅改变C处的直径,由Φ 180变到Φ 210时,描述该曲轴上的最大拉应力的变化的直线方程为:
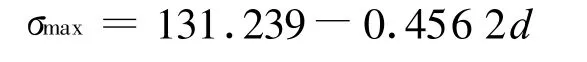
该方程粗略代表了曲轴压下冲压机时所受的最大拉应力随C处直径变化的基本走势,这对于研究当C处尺寸变化时,曲轴的最大拉应力是有很重要作用的,这个式子可以方便对C处的其它变化值进行研究分析,为曲轴的优化提供了非常有价值的参考资料,有助于对其受力情况进行评估。
[1] 周志鸿,李晓,孙常盛.基于ANSYS的曲柄压力机曲轴刚度分析[J].锻压技术,2007(5):120-123.
[2] 毛履国.压力机工艺系统刚度特性分析[J].锻压机械,2001(2):53-54.
[3] 史宝军,鹿晓阳,王保岭.开式压力机床身有限元分析与结构优选[J].力学与实践,2000(3):35-38.
[4] 娄路亮,李付国,李庆华.压力机曲轴的可靠性分析[J].锻压技术,1999(5):30-32.
[5] 李人宪.有限元法基础[M].北京:国防工业出版社,2002.
[6] Saccd Moaveni.有限元分析-ANSYS理论与应用[M].2版.王崧,董春敏,金云华,译.北京:电子工业出版社,2005.
[7] 龚曙光.ANSYS工程应用实例解析[M].北京:机械工业出版社,2003.
[8] 小飒工作室.最新经典ANSYS及Workbench教程[M].北京:电子工业出版社,2004.
