自适应周期滤波器及其学习算法

孙明轩，毕宏博

(浙江工业大学信息工程学院，浙江杭州310023)

0 引言

自适应滤波器自行调整滤波器参数，使滤波性能随时间逐步得以改善。根据优化准则不同，通常可分为两种算法［1、2］:最小均方算法和递推最小二乘算法。针对此两种自适应滤波算法的已发表结果多针对平稳过程。在实际应用场合，常常遇到所需处理的信号为非平稳随机变化的情形，这引起了人们的关注［3－7］。在非平稳随机信号中，有一类特殊的信号称为周期平稳随机信号，它的均值和自相关函数呈现周期性或几乎周期性。常用的处理方法是进行Fourier级数展开，采用Notch滤波器或Comb滤波器［8］。周期平稳随机信号可由平稳随机信号通过线性周期时变系统产生。因而，可借助于周期时变系统的Floquet理论来处理这类非平稳信号［9］，但这种方法限于线性系统。本文考虑被处理信号(期望响应)作为某周期时变系统输出的情形，为了获得其参数估计，采用周期学习机制(原则上适于非线性系统)［10、11］。提出周期最小均方(Periodic Least Mean Square，PLMS)和周期最小二乘(Periodic Least Squares，PLS)两种学习算法。本文首先给出自适应周期滤波器的一般结构及其学习机制的实现步骤，然后借鉴LMS算法和RLS算法的推导过程，给出PLMS算法和PLS算法，并完成仿真算例说明算法的有效性。

1 自适应周期滤波器

记di+kN(i=0，1，2，…，N－1;k=0，1，2，…)为滤波器在第k周期的期望响应，它由下述方式产生:

式中，xi+kN为n维输入向量，vi+kN为量测噪声;w+kN为n维权值向量，满足下述周期特性:

式中，Δwi+(k－1)N的确定取决于所考虑的优化问题的目标函数。常见的学习算法有两种:最小均方算法和最小二乘算法。

提出的周期学习机制的具体实现步骤如下:

(1)给定初始权向量值wi，i=0，1，…，N－1，并置k=0;

(2)在第k个周期，输入信号xi+kN，通过周期时变系统产生di+kN;

(3)施加相同的xi+kN，产生第k个周期的滤波器输出yi+kN，并计算Δwi+(k－1)N;

(4)依据学习算法计算下一周期的权值wi+kN(或wi+(k+1)N);

(5)检验迭代停止条件，若条件满足则停止运行;否则置k=k+1，转至S2。

2 周期学习算法

给出两种周期学习算法:一种是周期最小均方算法;另一种是周期最小二乘算法。

2.1 PLMS算法

由于考虑权值周期时变的情形，试图利用信号周期性，推导出PLMS算法，以提高滤波性能。考虑下述指标函数:

目标是选取wi+kN使得目标函数式5最小。利用负梯度策略，先得到指标函数J(wi+(k－1)N)关于wi+(k－1)N的瞬时梯度向量为:∇J(wi+(k－1)N)=－2ei+(k－1)Nxi+(k－1)N。依据式4，可得第k个周期i点的权值修正公式为:

式中，μ为学习增益。式6即PLMS算法。

2.2 PLS算法

借鉴递推最小二乘的推导过程，可以推导出PLS算法。因为考虑逐周期滤波误差的平方和为目标函数，需将各周期内i点相应的数值存储记录下来，为此定义:Di+kN=［di，d i+N，L，di+kN］T，Xi+kN=［xi，xi+N，L，xi+kN］T，由式1、2可得:

式中，Vi+kN代表各周期内i点的量测噪声。采用下述指标函数:

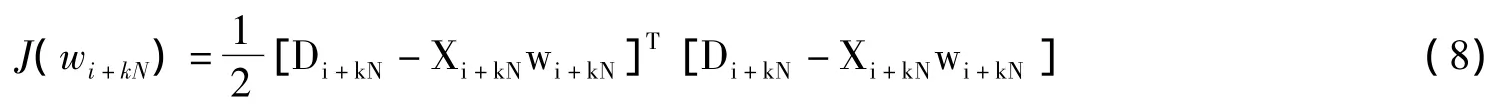
使式8最小，经计算可得:

式9得出的批处理算法可将获得的输入输出数据一次性处理，给出估计权值，但其中的求逆运算会使运算量随时间不断加大。参考递推最小二乘算法，构造周期最小二乘学习算法，以回避求逆运算。令:

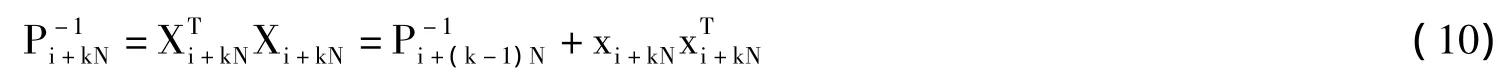
根据矩阵求逆公式(A+BCD)－1=A－1－A－1B(C－1+DA－1B)－1DA－1:

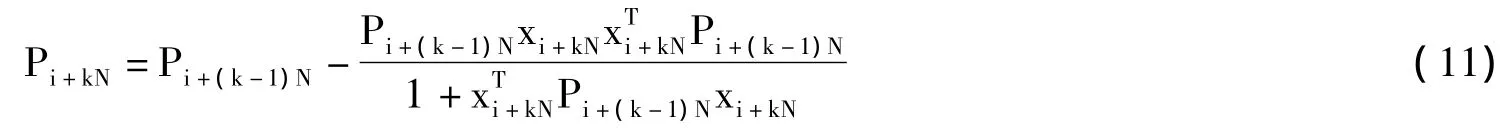
等式两边同乘xi+kN:

利用式9、10、12可得:

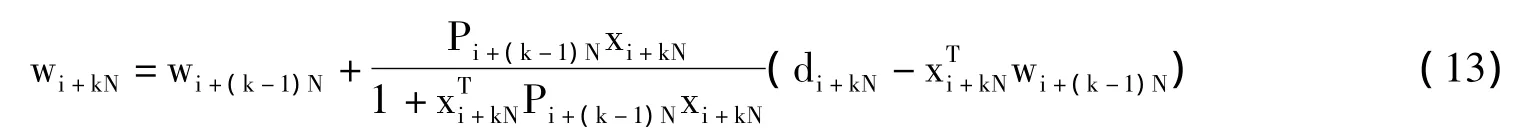
式11、13构成PLS算法。像期望的那样，这一算法中无矩阵求逆计算。上述推导类似递推最小二乘算法，但递推最小二乘算法是沿时间轴进行的，而学习算法是逐周期计算的。

3 数值结果

考虑期望响应d(n)=x(n)w1(n)+x(n－1)w2(n)+v(n)，其中，x(n)取值为［－1，1］上均匀分布的随机变量;权值w1(n)=1+0.1sin(2n/16)，w2(n)=0.5+0.1cos(2n/16)，周期N=16;取学习算法中的初始权值为w(n)=［0.1，0.1］T;量测噪声取为0.01randn(1)。仿真时，置时间区间为n∈{0，1，2，…，500}。

分别采用PLMS和PLS学习算法，检验自适应周期滤波器的滤波效果。PLMS算法的参数估计结果如图1所示，滤波误差如图2所示。为了比较，采用LMS算法时获得的结果如图3、4所示。

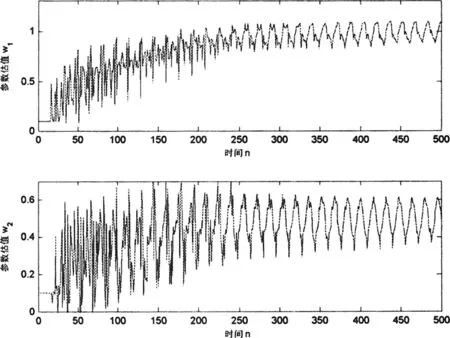
图1 参数估计

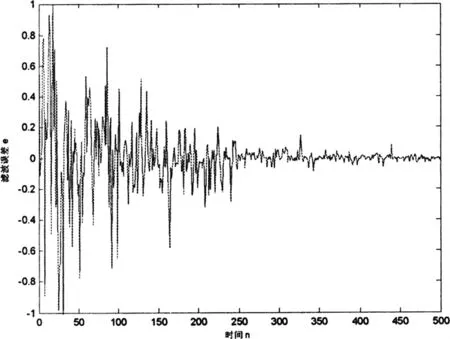
图2 滤波误差

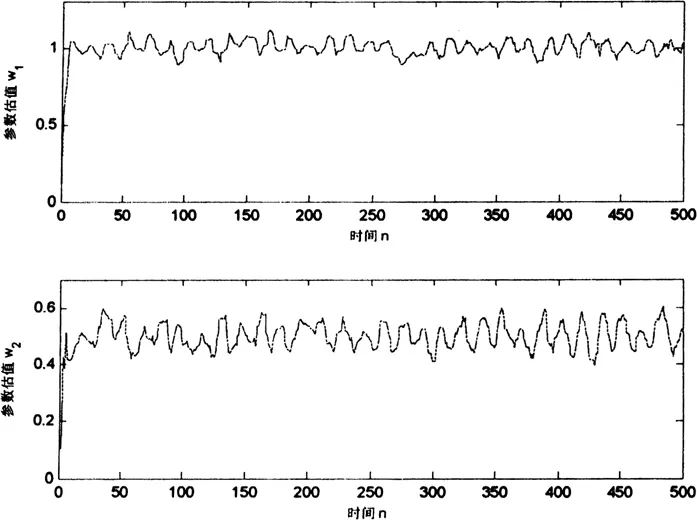
图3 参数估计

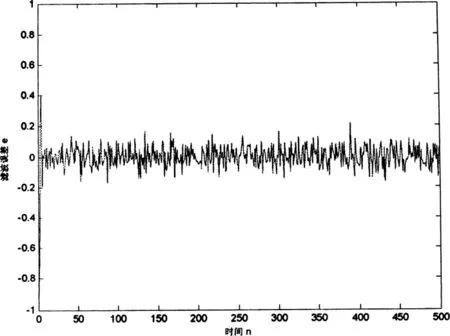
图4 滤波误差

采用PLS算法的参数估计结果如图5所示，滤波误差如图6所示。为了比较，采用RLS算法得到的结果如图7、8所示。

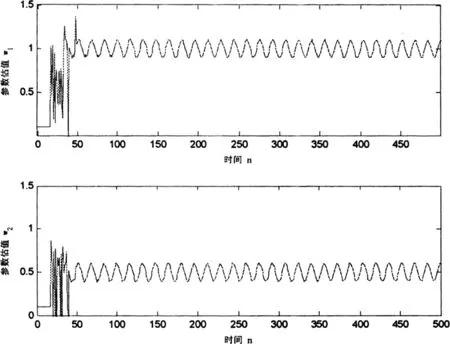
图5 参数估计

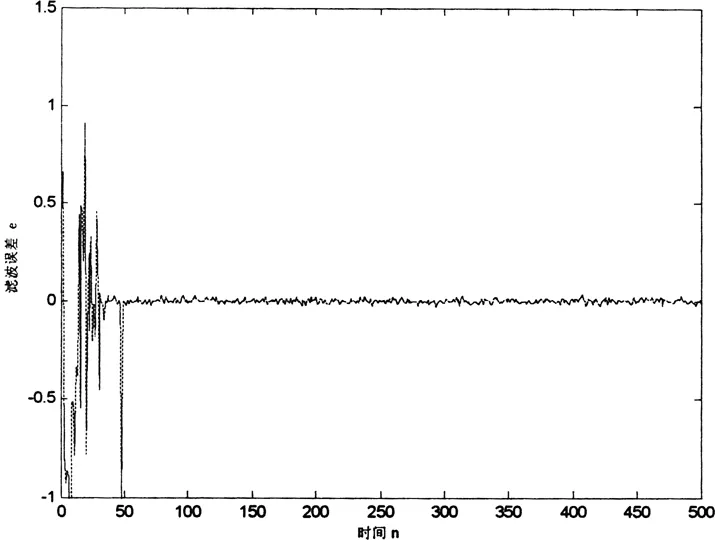
图6 滤波误差

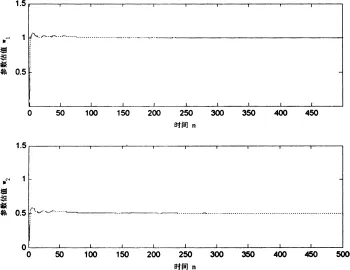
图7 参数估计

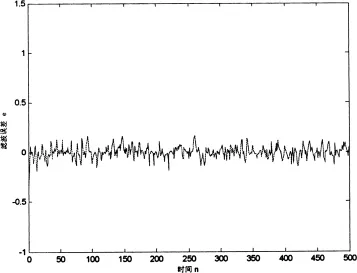
图8 滤波误差

从仿真结果看，与现有的滤波方法相比，采用基于PLS学习算法和PLMS学习算法的自适应滤波方法，对于周期平稳过程的滤波效果是显著的。

4 结束语

针对期望信号为周期平稳系统响应的滤波问题，本文提出了自适应周期滤波方法，采用周期学习机制构造了PLMS和PLS两种算法。通过仿真算例，与现有的滤波方法进行比较，说明了所提出的自适应周期滤波方法是适用的。

［1］Widrow B，Stearns S D.Adaptive Signal Processing［M］.Englewood Cliffs:Prentice Hall，1985:99－106.

［2］Haykin S.Adaptive Filter Theory［M］.Englewood Cliffs:Prentice Hall，2002:231－238.

［3］Widrow B，McCool J M，Larimore M G，etal.Stationary and nonstationary learning characteristics of the LMS adaptive filter［J］.Proceedings of IEEE，1976，64(8):1 151－1 162.

［4］Eweda E.Optimum Step Size of Sign Algorithm for Nonstationary Adaptive Filtering［J］.IEEE Transactions on Circuits and Systems，1990，38(11):1 897－1 901.

［5］Gazor S.Prediction in LMS-type adaptive algorithms for smoothly time varying enviroments［J］.IEEE Transactions on Signal Processing，1999，47(6):1 735－1 739.

［6］Godavarti M，Hero A O.Partial update LMS algorithms［J］.IEEE Transactions on Signal Processing，2005，53(7):2 382－2 399.

［7］Kivinen J，Warmuth M K，Hassibi B.The p-norm generalization of the LMS algorithm for adaptive filtering［J］.IEEE Transactions on Signal Processing，2006，54(5):1 782－1 793.

［8］Niedzwiecki M，Kaczmarek P.Generalized adaptive notch and comb filters for identification of quasi-periodically varying systems［J］.IEEE Transactions on Signal Processing，2005，53(12):4 599－4 609.

［9］Richards J A.Analysis of Periodically Time-Varying Systems［M］.New York:Springer-Verlag，1983:20－22.

［10］Sun M X，Ge S S.Adaptive repetitive control for a class of nonlinearly parametrized systems［J］.IEEE Transactions on Automatic Control，2006，51(10):1 684－1 688.

［11］孙明轩，王郸维，陈彭年.有限区间非线性系统的重复学习控制［J］.中国科学，2010，40(3):433－444.