一种基于稀疏重建的高分辨力方向估计方法

石绘红，章惠全，徐文

(浙江大学信息与电子工程学系，浙江杭州310027)

0 引言

利用传感器阵列进行源定位是当前一个热门研究领域，在声学、电磁学等领域得到了广泛应用，高分辨力是源定位技术的重要目标。目前源定位方法有很多［1］，但都存在一些缺点。近几年出现了利用目标信号在空间域的稀疏特性进行源定位的方法［2，3］，与传统方法相比，它们具有较高的分辨能力而且适用于任意阵形。其主要思想是将源位置离散化，定位问题转变为离散网格点上的信号强度求解问题。这类方法的关键是找到满足系统方程的稀疏解。根据压缩传感［4］理论，当观测矩阵满足等容受限原则［5］时，可以利用重建算法重建出稀疏信号。稀疏重建策略有贪婪算法［6］和凸优化算法［7］等。本文主要考虑单频信号、时域采样且波源不相关情况下的波达方向估计(角度空间的源定位)，基于数据相关矩阵建立观测方程，利用1-范数约束和凸优化方法重建信号的空间谱，从而获得DOA的估计。进一步采用了局部网格细化方法，增加分辨力且降低算法计算量。由于采用相关矩阵R和1-范数，本文称之为l1-R方法，与现有的同类方法相比，l1-R方法具有最小的求解维度和更好的估计性能。最后，本文通过数值仿真验证了该方法的高分辨能力以及近似最优的性能。

1 问题描述

假设有一接收传感器阵列，阵元数为M，有K个频率为ω的单频信号sk，k=1，2，…，K，分别以θ1，θ2，…，θK的入射角度到达接收阵。考虑远场情况，阵列接收到的信号可表示为:

式中，y=[y1，…，yM]T，hk=[eφ1(θk)，eφ2(θk)，…，eφM(θk)]T为第k个信号的阵列响应向量，φm(θk)为入射角为θk的信号到第m个阵元的相移函数，w为高斯白噪声。考虑多次快拍的情况，可以写成矩阵形式:

式中，Y=［y1，y2，…，yL］，H=［h1，h2，…，hK］，S=［s1，s2，…，sL］，sl=［s1(l)，s2(l)，…，sK(l)］T，W=［w1，w2，…，wL］，l=1，2，…，L为快拍数。若每次快拍统计独立，各信号之间不相关，有:

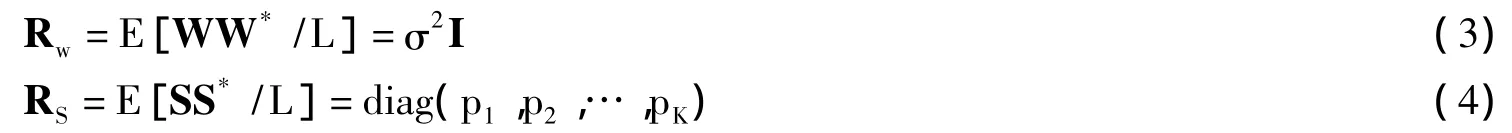
式中，E［·］表示期望，I为单位矩阵，σ2为噪声方差，diag(·)表示对角矩阵，pk为第k个信号的功率。

DOA估计问题即是要求解H中的K个信号的角度θ1，θ2，…，θK。基于传统波束形成的方法，如Bartlett、最小方差无偏(MV/Capon)方法采用“驾驶向量”的思想，用hk的拷贝与阵列信号Y进行相关运算，以估计信号方向，其中MV/Capon方法由于利用了数据相关矩阵信息，相比与Bartlett方法具有较高的分辨能力;基于子空间的方法，如MUSIC，通过对相关矩阵做特征分解获得信号子空间与噪声子空间，然后估计信号方向，这类方法一般需要信号的个数作为先验信息，而且与MV/Capon方法类似对SNR及信号相关性较敏感;基于最大似然(ML)估计的参量方法通过最大化似然函数来同时估计所有信号方向，这类方法具有最优的统计性能，但基于非凸优化，计算量很大，同时也需要信号个数的先验信息;还有一些其它方法，如Root-MUSIC、ESPRIT等方法，具有较高的分辨能力，但它们一般只适用于均匀直线阵(ULA)的情况。

本文将DOA估计问题表示成一个高度欠定方程的求解问题，利用源信号在角度空间域的稀疏特性，寻找满足观测方程的最稀疏解，从而获得信号方向的估计。

2 基于稀疏重建的方向估计

本文将感兴趣的角度区域离散化为N个网格点，网格点数大于信号数(N＞K)，假设所有DOA都在网格点上。与式1类似，阵列接收到的信号可以表示为:

式中，hn对应角度为θn上信号sn的阵列响应向量，若θn方向不存在信号，则sn为零，所以只有K个非零的sn，该式与式1等价。同样考虑多次快拍的情况，有与式2相同的表示式。此时，式2是一个有无穷多解的欠定方程，但由于实际信号S是稀疏的，所以要寻求该欠定方程的最稀疏解。

式2中需要求解的S是一个N×L维复数矩阵，计算量很大，希望可以降低S的维度。提出了l1-SVD方法［2］，将S维度降至N×K。本文考虑根据式2得到:

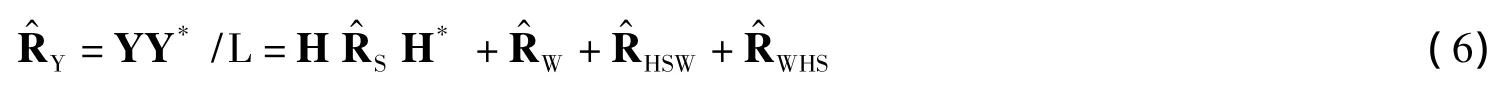
要寻求满足方程式7的最稀疏解，严格来说是要求解最小化0-范数的组合优化问题，但实现上比较困难。实际中采用较多的是退化的0-范数最小化，即通过下式求解b:

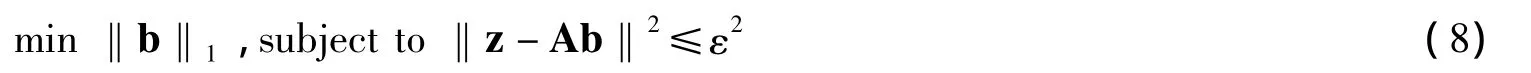
式中，规化常数ε2需要根据噪声强度适当选择，若ε2太小，算法对噪声很敏感，若ε2过大，导致重建结果全为零。式8可以通过凸优化方法求解，如二阶圆锥规化(SOCP)等。

基于稀疏重建的方向估计方法的分辨能力依赖于网格间隔，整个搜索区域内细化网格会增加计算量。本文采取了先使用简单且对SNR不敏感的Bartlett方法实现粗糙的方向估计，然后在信号较可能出现的区域细化网格［2］，以增加分辨能力且降低算法的计算量。

整个求解实现过程框图如图1所示，首先用Bartlett方法预定位，然后在信号较可能出现的区域形成局部细化的网格，并构建系统方程7，最后用SOCP算法重建信号的空间谱。

图1 l1-R方法的实现框图

3 数值仿真

本文仿真采用半波长间隔的ULA，阵元数M=20，快拍数L=32。

用l1-R方法估计方向如图2所示。源数目为3，DOA分别为0°、5°和25°，强度均为1，噪声为白高斯噪声，方差σ2=4。先用Bartlett方法预定位，在其主瓣－5°～10°和20°～30°范围内网格细化到0.5°，再进行稀疏重建，可见该方法可以较精确地重建出信号方向和幅度。

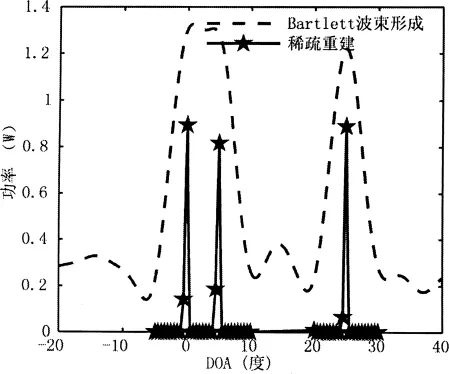
图23 个源目标的l1-R方位估计结果

估计偏差和均方误差(MSE)的性能仿真分析分别如图3、图4所示。MUSIC、l1-R、l1-SVD这3种方法在不同源间隔情况下的估计偏差比较如图3所示。假定已知源数目为2，角度较小的称为源1，角度较大的称为源2，源强度相同，SNR为20dB，源位置在－10°～10°区间随机产生，每种情况各进行200次蒙特卡罗仿真。从图3中可以看出，当源间隔为1°时，MUSIC和l1-SVD方法有较大的估计偏差，随着源间隔的增加MUSIC方法的估计偏差减小，但l1-SVD方法只能无偏地估计间隔足够大的源;与l1-SVD和MUSIC方法比较，l1-R方法具有较小的估计偏差。当源数目为2，间隔为3°时，l1-R和l1-SVD、MUSIC等一些其他方法在不同噪声方差下的MSE，以及与Cramér-Rao下限(CRB)的比较如图4所示。MSE的定义是err2=∑(－θk)2/K。源强度均为1，每种情况各进行500次蒙特卡罗仿真，其中，l1-R、l1-SVD方法在Bartlett主瓣内划分41个网格，其他参数与图2中相同。从图4中可以看出，Bartlett方法具有较低的分辨力;MV和MUSIC方法在噪声方差较小时，性能接近CRB;除了噪声较小的情况(此时，l1-R的误差主要由网格精度引入，l1-SVD的误差主要由估计偏差引入)，l1-R和l1-SVD方法性能接近于CRB和ML方法，具有近似最优的性能;此外，l1-R方法具有较高的RMS，其性能优于l1-SVD方法。总之，l1-R方法具有较高的RMS和SNR，估计性能较好;采用了局部网格细化方法，分辨能力较高;此外，它与ML方法性能近似，但其计算量小于ML方法。

4 结束语

本文提出了基于稀疏重建算法的DOA估计方法——l1-R方法。该方法充分利用了目标信号在空间域的稀疏特性，基于数据相关矩阵建立系统方程，用1-范数约束目标的稀疏性，经重建算法能够得到很好的估计性能。本文通过数值仿真验证了l1-R方法的有效性、高分辨能力和近似最优性。本文提出的方法对实际应用具有较好的借鉴作用。

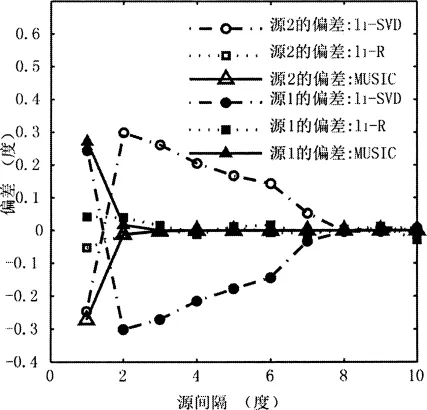
图3 不同源间隔下的估计偏差

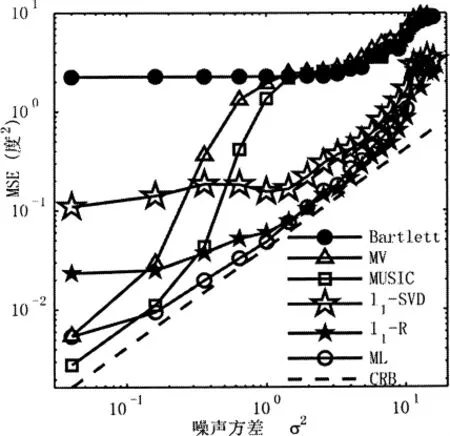
图4 不同噪声方差下的均方误差

［1］Krim H，Viberg M.Two decades of array signal processing research the parametric approach［J］.IEEE Signal Processing Magazine，1996，13(4):67－94.

［2］Malioutov D，Cetin M，Willsky A S.A sparse signal reconstruction perspective for source localization with sensor arrays［J］.Signal Processing，2005，53(8):3 010－3 022.

［3］Gurbuz A C，McClellan J H，Cevher V.A compressive beamforming method［C］.Las Vegas NV:IEEE International Conference，Acoustics，Speech and Signal Processing，2008:2 617－2 620.

［4］Candes E J，Wakin M B.An introduction to compressive sampling［J］.IEEE Signal Processing Magazine，2008，25(2):21－30.

［5］Candes E J，Romberg J K，Tao T.Stable signal recovery from incomplete and inaccurate measurements［J］.Pure Applied Mathematics，2006，59(8):1 207－1 223.

［6］Tropp J A，Gilbert A C.Signal recovery from partial information via orthogonal matching pursuit［J］.Information Theory，2007，53(12):4 655－4 666.

［7］Boyd S，Vandenberghe L.Convex Optimization［M］.Cambridge UK:Cambridge Univ.Press，2004:561－615.