基于搜索的RSSI节点定位算法

蔡优笔，王建中

(杭州电子科技大学信息与控制研究所，浙江杭州310018)

0 引言

在无线传感器网络中，位置信息对无线传感器网络的监测活动至关重要，节点的位置信息也是基于位置信息的路由算法的前提。现有定位技术中，一般是利用无线传感器网络中少量已知的节点来获取其它未知节点的位置信息。位置已知的节点称为锚节点，位置未知的节点称为未知节点。一般来说，目前的定位算法可以分为两类:基于测距的定位算法和无需测距的定位算法［1］。基于测距的定位算法通过测量节点间的距离或角度信息，使用三边测量、三角测量或极大似然估计定位法计算节点位置典型的测距技术有RSSI，TOA，TDOA和AOA等;无需测距的定位算法主要是利用节点间的几何拓扑关系、连通信息或网络多跳路由来估计节点位置。主要有凸规划、质心算法、DV-hop算法、Amorphous算法、APIT算法等。基于RSSI的测距技术，因传感器节点本身具有无线通信能力，而且一般的无线射频电路本身具备RSSI的测量功能，无需额外的硬件，是一种低功率、廉价、实现简单的测距技术，是目前研究的热点，同时也得到了业界的广泛应用。例如:微软研发中心的Radar定位系统［2］，哈佛大学的MoteTrack定位系统等［3］。本文在充分研究现有基于RSSI定位算法的基础上，通过对无线电传播路径损耗模型的分析，提出了一种定位精度高，成本较低的基于搜索的RSSI节点定位算法。

1 基于搜索的RSSI节点定位算法

1.1 RSSI测距原理及问题分析

基于RSSI的测距原理是依据无线信号传播路径损耗模型进行节点间距离的估计［4］。由于无线信号在传播过程中存在多径、绕射、障碍物等因素，一般采用对数－距离路径损耗模型。

式中，Ls(d)表示经过了距离d后的路径损耗，单位为dBm;Ls(d0)表示经过了距离d0(通常d0取1m)后的路径损耗，单位为dBm;Xσ为均值为零，方差为σ2的高斯随机分布函数，n为无线电传播路径损耗系数，一般取2。

由式1得:

式中，A1表示参考距离d0=1m时，节点接收到的无线信号强度，RSSI为多次RSSI值的均值。

由以上分析可知，决定RSSI测距精度的因素有两个:一是减少噪声Xσ和多径传输对RSSI测量值的影响，提高RSSI测量精度;二是精确估计出式2中反映定位区域内信号传输特性的路径损耗模型参数A1和n。

1.2 路径损耗模型参数估计与定位

路径损耗模型参数估计原理如图1所示:M为未知节点，三角形BiBjBk的3个顶点Bi，Bj，Bk分别为距离未知节点M最近的3个锚节点。锚节点Bi，Bj，Bk两两之间能够互相通信，距离分别为dij，dik，djk。利用锚节点的位置信息来估计该定位区域内路径损耗模型参数A和n，再根据式2计算未知节点M与锚节点Bi，Bj，Bk之间的距离di，dj，dk，实现未知节点与锚节点间的测距并提高未知节点与锚节点之间的测距精度。

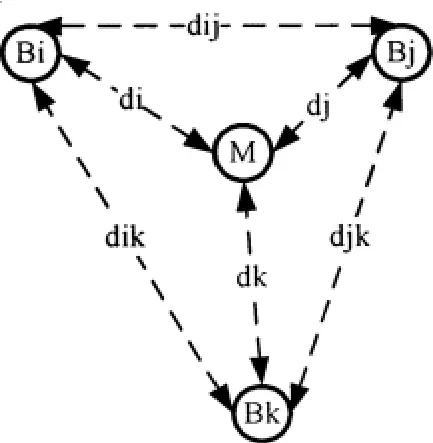
图1 路径损耗模型参数估计原理图

三角形BiBjBk区域内路径损耗模型参数A和n的估算实现如下:图1中，假定RSSIi，RSSIj，RSSIk分别是未知节点M接收到的已知锚节点Bi，Bj，Bk的信号的RSSI值，RSSIab，dab分别是已知锚节点Ba接收到的已知锚节点Bb的信号的RSSI值和锚节点Ba，Bb之间的距离(a，b=i，j，k)，di，dj，dk分别是未知节点M与锚节点Bi，Bj，Bk之间的距离。

则存在如下关系:

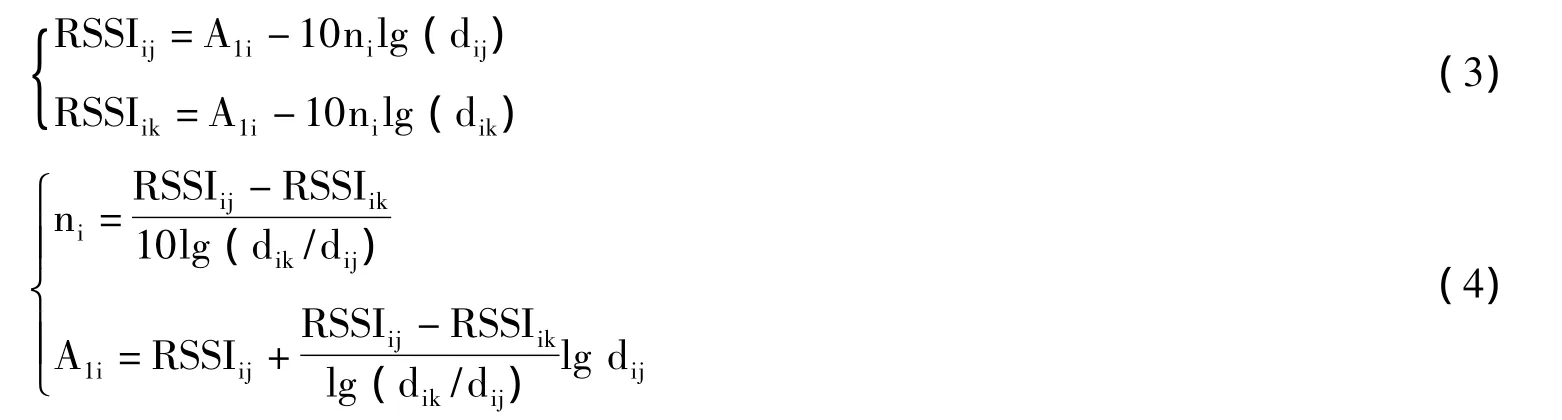
同理可得到三角形BiBjBk中另两个锚节点相对应的nj，A1j和nk，A1k。为了简单起见，取三角形BiBjBk区域的路径损耗模型系数如下:

将A1，n以及RSSIi，RSSIj，RSSIk的值代入式2计算未知节点M与锚节点Bi，Bj，Bk之间的距离di，dj，dk，用三角形质心定位算法计算出未知节点M的位置坐标。

1.3 定位坐标的循环求精

为了减小测距误差对定位的影响，提出了两种循环求精定位算法——Cooperative ranging和Two-Phase positioning［5］。

本文提出一种基于概率计算法搜索未知节点的最终坐标。具体过程为，建立未知节点的分布概率模型:

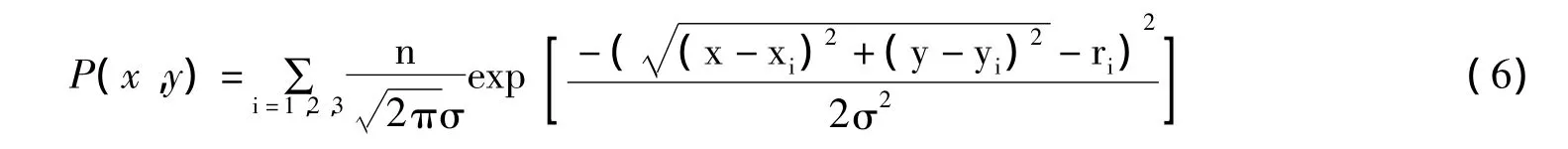
式中，P(x，y)是未知节点在无线传感器网络中(x，y)处的分布概率，n为无线电传播路径损耗系数，(xi，yi)是第i个参考节点的坐标信息，ri是未知节点到第i个参考节点的距离，σ是功率测量误差标准差。

将定位计算阶段得到的未知节点坐标代入式6，得到未知节点M在(x0，y0)的分布概率，再以L1为步长，分别得到(x0+L1，y0)、(x0，y0+L1)、(x0－L1，y0)、(x0，y0－L1)处的分布概率，选择以上5个坐标中最大的分布概率所对应的位置坐标作为此次的定位位置(x1，y1)。

重复以上搜索，步长为Ln=0.5Ln－1，直到第N次的定位位置(xn，yn)与第(N－1)次的定位位置(xn－1，yn－1)相同则停止定位搜索处理，并将第N次的定位位置(xn，yn)作为未知节点的最终坐标。

2 仿真

利用Matlab对本文所述定位算法仿真。分别用基于RSSI三角形质心定位算法和本文所提出的定位算法对区域内的未知节点进行定位，最终获得两种定位算法的平均定位精度，如图2所示。

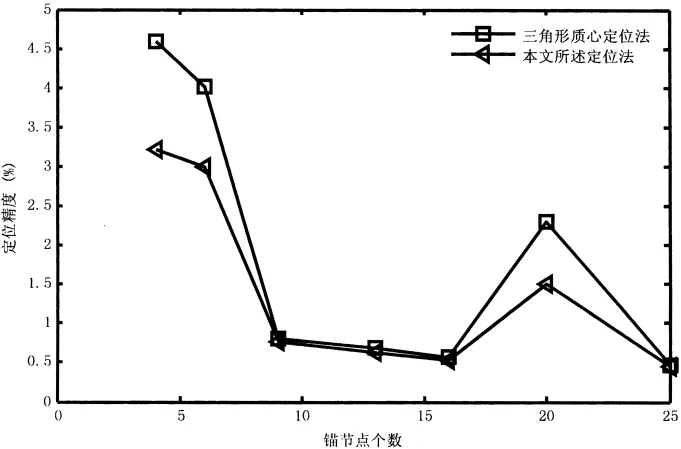
图2 定位算法仿真图

从图2可得知，本文所提出的基于搜索的RSSI定位算法，定位精度在锚节点个数相同的情况下，较传统的基于RSSI的三角形质心定位算法有一定的提高，在锚节点个数为4个和20个时，提升较大。

3 结束语

本文提出的基于搜索的RSSI定位算法，以锚节点之间的精确信息求取无线信号传播路径损耗模型参数，极大减小未知节点的测距误差，在循环求精过程中，引入未知节点坐标概率计算来获取未知节点的最终坐标，和传统的定位算法相比，在增加一点点通信开销和计算开销的情况下，对未知节点的定位精度有所提升。仿真表明:本算法简单，定位精度高，对硬件要求成本低，无需硬件扩展，满足无线传感器网络低成本，低功耗的要求。

［1］He Tian，Huang Chengdu，Blum Brian M，etal.Range-Free localization schemes for large scale sensor networks［C］.New York.Proceedings of the 9th Annual International Conference on Mobile Computing and Networking.2003:81－95.

［2］Bahl P，Padmanabhan V N.RADAR:an in-building RF-based user location and tracking system［C］.Tel Aviv.Proceedings of the Nineteenth Annual Joint Conference of the IEEE Computer and Communications Societies.2000:775－784.

［3］Lorincz Konrad，Welsh Matt.MoteTrack:a robust，decentralized approach to RF-based location tracking［J］.Personal and Ubiquitous computing.2007，11(6):489－503.

［4］陈维克，李文锋.基于RSSI的无线传感器网络加权质心定位算法［J］.武汉理工大学学报，2006，30(2):265－268.

［5］Chris Savarese，Jan M.Rabaey，Jan Beutel.Locationing in distributed ad-hoc wireless sensor networks［C］.Salt Lake.Proceedings of the 2001 IEEE international conference on acoustics，speech and signal processing.2001:2 037－2 040.

［6］梁玉琴，曾庆化，刘建业.基于UKF滤波的WSN节点定位研究［J］.传感技术学报，2010，23(6):878－882.