基于粒子-蒙特卡洛模型的气体电子倍增探测器的研究

杨兰兰 屠 彦 张盼盼 秦娜娜 蔡国龙 陈仲珊 马善乐

(东南大学电子科学与工程学院 南京 210096)

气体探测器技术已进入蓬勃发展的新时期，出现微条气体探测器、微间隙气体探测器、微网结构气体探测器、气体电子倍增探测器(Gas Electron Multiplier, GEM)等新型气体探测器。其中，欧洲核子研究中心(CERN)的Sauli等[1]1997年发明的气体电子倍增探测器，在加速器的粒子追踪、时间投影室的读出探测器、中子检测、医用CT诊断、X射线晶体学、暗物质检测等领域呈现出广阔的应用前景，成为研究热点。

由于结构的限制，多丝正比室无法满足高光度条件下的高分辨率和高计数率要求；微条气体探测器、微间隙气体探测器工作在高增益时，易出现打火，工作不稳定的缺点。而GEM探测器可以多个GEM膜级联使用，将信号多次放大，从而大幅度提高增益，也可降低GEM探测器发生连续放电造成损伤的几率，这一特性使GEM探测器具有稳定的高增益。GEM探测器空间位置分辨率可达30 mm，计数率可达100 MHz/cm2，可满足高光度条件下的高分辨率和高计数率要求。GEM还有如下优点：探测器信号纯由电子放大产生，因此非常快，时间分辨率可达5 ns；GEM膜的柔软性可使其弯曲以适合各种特殊形状探测器的需要；放大电极和读出电极分开，可避免信号放大和读出之间的相互干扰，使信号读出方式灵活；工艺简单，制作方便，重量轻，成本低，寿命长[2,3]。

然而，GEM的测试手段无法定量分析一些特性参数，也无法定量解释GEM雪崩的限制、增益的不稳定性等，因此，GEM探测器的研究与优化就主要利用计算机模拟，如电场分析、物理机理的探讨、有效增益等特性参数的模拟分析等，这些模拟研究为GEM结构的优化和发展奠定了一定的基础。

除在某些特定参数性能的分析上利用简单的流体模型或粒子模型进行分析和模拟外，绝大多数的理论研究都基于欧洲核子研究中心开发的GARFIELD软件。但该软件有其局限性，很难对GEM的物理机理作更深入的探讨，因此须用更符合GEM探测器中粒子运动规律的方法进行模拟。PIC模拟(particle-in-cell simulation)，是模拟Maxwell方程组描述系统演进的有效方法。PIC-MCC模拟是在PIC模拟的基础上增加了带电粒子与中性粒子间的碰撞过程，而这个过程用Monte Carlo方法来模拟[6]。以粒子-蒙特卡罗(PIC-MCC)模型用计算机模拟跟踪大量单个微观粒子的运动，再对组成物体（气态，液态、固态和等离子体态）的大量微观粒子进行统计平均，由此得到宏观物体的物质特性和运动规律。PIC-MCC法已成为研究气体放电领域的强有力工具。

本文将基于PIC-MCC模型探讨GEM探测器的倍增过程，并分析模拟结果和GEM的性能参数的关系，为后续的研究建立理论基础。

1 理论基础及GEM的结构模型

1.1 PIC-MCC方法

图1所示为PIC-MCC方法的计算流程。如图1所示，假设大量的带电粒子具有初始位置xi和速度 vi，对它们统计平均求出空间的电荷rj和电流密度分布Jj，再通过麦克斯韦方程组：

求出各处的电场 Ej和磁场 Bj，这样，每个粒子所受的洛伦兹力Fi就知道了：

粒子所在的空间位置和自身的速度可以用牛顿运动方程来获得[7,8]，其中g为相对论系数。

而下一时刻每个粒子的位置和速度可通过运动方程求出。在此考虑粒子遇边界的处理（吸收或激发），并考虑带电粒子与中性粒子间的碰撞过程，该过程系由Monte Carlo法模拟。如此循环进行，跟踪计算大量带电粒子的运动，再根据感兴趣问题对这些大量带电粒子的某些物理量作统计平均，即可得到宏观的物质特性和运动规律[9]。

图1 PIC-MCC方法计算流程Fig.1 PIC-MCC simulation algorithm.

1.2 GEM的结构模型

图2 是 GEM 膜的俯视图和纵剖面图[10]，其由中间的Kapton 膜(标准尺寸为50 mm)和上下两层铜膜(标准尺寸为5 mm)组成，通过一定的工艺在膜上均匀地制作出双圆台孔(Φ70 mm +Φ50 mm)，孔间距为140 mm。在上下两层铜膜上加一定电压，就能在孔中产生强电场，空间电子在电场的作用下漂移，经过孔时发生雪崩，从而实现电子倍增放大。

图2 GEM探测器的俯视图和纵剖面图Fig.2 The top view and cut-away section view of GEM.

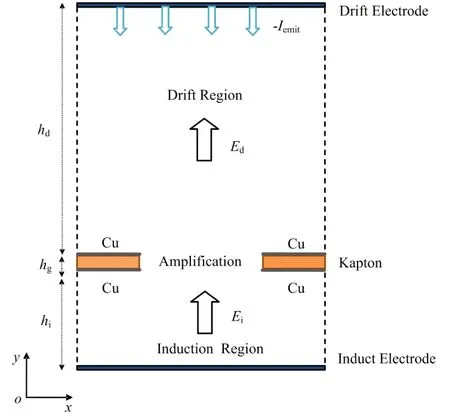
图3 GEM的二维结构模拟示意图Fig.3 Two-dimensional schematic structure of GEM.

考虑到 PIC-MCC模拟耗时较长，本文采用简化的GEM模型(图3)：微孔为圆柱形，直径70 mm；截取一个微孔单元以及周边宽35 mm的Kapton膜(即微孔间距为140 mm)，连同GEM微孔上方的漂移区和下方的收集区构成一个模拟单元；铜膜厚度仅为5 mm，忽略铜膜的厚度，保留铜膜的属性。在上下铜膜上施加电压Vgem=300 V，漂移电极上施加电压 Vd=−360 V，设有初始电流 Iemit=1.28´10−6A从漂移电极上发射(由8000个初始电子产生)，发射脉冲宽度为1 ns。收集电极上施加电压Vi=40 V，收集在GEM微孔中倍增放大的粒子。由于在漂移区和收集区的大部分区域里均为均匀的电场，而粒子模拟耗时较长，因此模拟时采用漂移区高度hd=600 mm ，收集区高度 hi=200 mm， Kapton 膜的高度为hg=50 mm。由上述参数设置，可认为GEM漂移区电场Ed=1 kV/cm，收集区电场Ei=2 kV/cm（实际漂移区和收集区电场并非完全的均匀场，与上述电场值会略有差别，但可用电压/距离来粗估电场）。

在伯克利大学PTSG组开发的XOOPIC软件内核基础上，改进了对本组已有的基于二维PIC-MCC模型的PDP(Plasma Display Panel)粒子模拟软件进行，使其适合GEM的模拟。尝试从跟踪粒子运动和用 Monte Carlo方法模拟粒子间的碰撞来模拟GEM中的电子的倍增放大过程。模拟时选择时间步长为10−13s，空间步长为5 mm，所充气体为一个大气压的纯氙。

2 模拟结果及讨论

2.1 GEM中的电场及粒子倍增放大过程

图4 GEM的中等位线分布(a)、微孔附近的等位线分布(b)，及其电场强度随y的变化(c)随x的变化(d)Fig.4 The potential distribution in (a) and around (b) a GEM hole, and the electric field variation in the y (c) and x (d) direction.

图4为上述结构和模拟条件下计算得到的GEM的等位线分布。漂移区和收集区的电场使电子有向下的加速度，电子在往收集电极运动的过程中，被GEM微孔中心的强电场倍增放大。由图4(a)、(b)，在漂移区绝大部分区域内，等位线均匀分布，也即漂移区的电场主要由漂移电极和膜上铜膜的电压决定，仅在微孔附近由于微孔中心强电场的影响，等位线向上弯曲，从而对电子产生会聚作用，使更多的一次电子进入微孔倍增放大。在收集区的绝大部分区域内，等位线也均匀分布，仅在微孔附近由于微孔中心强电场的影响，等位线向下弯曲，使在微孔中倍增放大的电子在进入收集区后扩散开来。图4(c)给出了微孔中心及微孔附近的电场强度随小孔轴向y的变化，微孔中心轴x=70mm处的电场强度最低，微孔边缘处（靠近铜膜电极处）的电场强度最高，此由尖端效应造成[11]。图4(d)给出了微孔中心(y=225mm)及微孔附近的电场强度随x的变化，同样是微孔边缘处的电场强度要远远大于其他地方的值，这易使微孔边缘处发生放电，所以文献[12]的方案为铜膜电极的开孔半径略大于GEM的微孔半径，以有效抑制微孔边缘处的放电，提高 GEM的增益。

图5为GEM空间中电子和Xe离子数目随时间的变化关系。在约24 ns处，一次电子开始陆续进入GEM微孔中间的强电场区域，电子发生雪崩放大，空间电子和离子的数目急剧增多。在此倍增放大过程中，一部分电子会打到 GEM 微孔边界的Kapton介质层上而损失，并在介质层上形成电荷积累，另一部分被GEM微孔下方的铜电极吸收。由于电子的运动速度较快，大部分电子将通过 GEM微孔到达下方的收集电极而被收集，GEM空间中的电子数目先增后降，最后完全被介质层和电极吸收，空间电子数为零。此倍增放大过程中，空间的离子由于运动速度较慢，相同时间内被介质层和电极收集到的离子数目非常少，空间中的离子数目会持续增加，并慢慢趋于饱和。电子倍增过程结束后，空间的 Xe离子在电场作用下仍然向漂移电极方向运动，并有部分离子被Kapton介质层和GEM微孔上方的铜电极吸收，此时离子的数目会慢慢的下降，但这一过程将持续至ms量级。

图5 GEM空间中电子和Xe离子数目随时间的变化关系Fig.5 Number of electrons and xenon ions vs time.

图6 电子和Xe离子的空间分布随时间的变化情况Fig.6 Space distributions of electrons and xenon ions at different nanoseconds.

图6给出了电子和Xe离子的空间分布随时间的变化情况，该空间分布及运动变化对应于图5的空间粒子数的变化，对应时刻为t1=10.1 ns, t2=32.1 ns, t3=50.5 ns, t4=83.4 ns，t5=94.8 ns。由图 6 可见，当部分一次电子进入GEM微孔的强电场区域发生雪崩放大时，空间的电子和离子数目开始急剧增加。但由于电子的运动速度较快，有的电子在倍增放大时，有的电子仍在漂移区，而倍增放大后的电子则有的被微孔的Kapton介质层吸收，有的被电极吸收，这与前文的分析一致。而微孔空间的离子运动速度较慢，被介质层和电极吸收的数量较少，倍增产生的离子大多还分布在空间中，所以离子的空间分布也可形象地显示出电子的倍增效应。

2.2 GEM的增益

GEM 的增益是重要参数指标，其包括总增益和有效增益。GEM的总增益定义为在GEM的倍增放大过程中产生的总电子数Nt与初始电子Np的比值，即 Gt= Nt/Np；有效增益则是 GEM 的收集电极收集到的电子数 Neff（即产生有效读出信号的电子数）与初始电子Np的比值，即Geff= Neff/Np。

在漂移区向GEM微孔运动的过程中，部分一次电子(Ncuu)会被GEM网格孔上方的铜电极吸收，无法进入小孔进行倍增放大，而进入小孔的一次电子也有一部分(Nd)被GEM微孔的Kapton介质层吸收，还有被微孔下方铜电极吸收的电子(Ncud)，剩下的大部分电子 Neff到达收集电极产生有效的电流信号。在图3的结构和电场情况下，各电极和介质层收集到的电子数的模拟结果为：Nd=125900，Ncuu=0，Ncud=512000，Neff=102400，Nt= 740300。则在上述模拟条件下，一次电子100%进入GEM网格孔，所以Ncuu=0，总增益Gt=93，有效增益Geff=13，有效增益占总增益的比例为17%，这使得被收集电极收集到的电子比例很低。因此GEM的电场分布，特别是由收集极电压和GEM膜间电压决定的GEM下电极附近区域的电场分布，对GEM的有效增益影响很大。在其他条件不变的情况下，调整使得收集区电场Ei=4 kV/cm，则有效增益占总增益的比例可提高到35%，有效增益Geff提高到38。由此可知，GEM的电场参数对GEM的特性有很大影响，对同样的GEM结构，优化电场参数可提高GEM的性能，后续的工作还会对此进行详细的研究。

3 结论

GEM作为一种新型的气体探测器以其高增益、高计数率、高空间分辨率、良好成像特性等优势在粒子物理和辐射成像等领域具有广泛的应用前景，针对GEM的研究已从粒子物理领域扩展到其他许多领域。本文利用粒子-蒙特卡罗模型对GEM中的电子倍增过程进行研究，从微观角度更深入的了解GEM的物理机理，并初步建立了GEM的总增益和有效增益与微观粒子个数和分布之间的关系，即建立起宏观的性能参数和微观粒子之间的关联。本文仅是基于粒子-蒙特卡罗模型对GEM研究工作的一个开端，后续将对GEM的结构、电场、雪崩机制、电荷堆积机制等做进一步的研究。

1 Sauli F.A new concept for electron amplification in gas detectors [J].Nucl Instr Meth, 1997, A386: 531

2 Bachmann S, Bressan A, Kappler S, et al.Development and applications of the gas electron multiplier [J], Nucl Instru Meth, 2001, A471: 115–119

3 Sauli F, Development and applications of gas electron multiplier detectors [J], Nucl Instru Meth, 2003, A505:195–198

4 Sharma A.3D simulation of charge transfer in a Gas Electron Multiplier(GEM) and comparison to experiment[J], Nucl Instru Met, 2000, A454: 267–271

5 Bouianov O, Bouianov M, Orava R, et al.Progress in GEM simulation [J], Nucl Instru Meth, 2000, A450:277–287

6 Vahedi V, Surendra M.Monte Carlo collision model for particle-in-cell method: application to argon and oxygen discharges [J], Comput Phys Commun, 1998, 87: 179–198

7 Birdsall C K, Langdon A B.Plasma Physics via Computer Simulation [M], New York: McGaw-Hill, 1985

8 Buneman O.Time reversible difference procedures[J], J Comput Phys, 1967, 1: 517–535

9 邵福球.等离子体粒子模拟[M], 北京: 科学出版社,2002, 2 SHAO Fuqiu, Plasma particle simulation [M], Beijing:Science Press, 2002,2

10 http://gdd.web.cern.ch/GDD/gemframing.res/gem_assem bly.pdf, [OL] 2011.4.30125

11 周意, 李澄, 安少辉, 等.GEM 电极的三维电场分布计算[J].高能物理与核物理, 2004, 28(3): 299–303 ZHOU Yi, CHENG Li, AN Shaohui, et al.GEM electrode calculated three-dimensional electric field distribution [J],High Energy Physics and Nuclear Physics, 2004, 28(3):299–303

12 Breskin A, Alon R, Cortesi M, et al.A Concise review on THGEM detectors [J], Nucl Instr Meth, 2009, A598:107–111