基于Geant4模拟质子在半导体Si材料中的NIEL值
2011-03-24王同权王兴功刘雪林
路 伟 王同权 王兴功 刘雪林
1(解放军疾病预防控制所 北京 100071)
2(北京清河大楼子7 北京 100085)
由位移能量损失引起的位移损伤效应,会改变半导体材料的特性参数,半导体、光感器件等在辐射场中的位移损伤依赖于灵敏体内沉积的位移能量损失值。经验表明,对于大多数器件、入射粒子类型,损伤因子和非电离能损 (Non-ionizing Energy Loss, NIEL)呈线性关系,位移损伤的计算归结为NIEL和粒子通量的计算,器件的NIEL相关性研究成为位移损伤效应分析的趋势[1]。
模拟质子对半导体器件位移损伤的关键,是给出入射质子在器件内的总位移能量沉积。NIEL对于总位移能量损失类似于LET对于电离能量沉积,20年来,NIEL与入射质子能量的关系由 Burke、Dale、Insoo Jun等人用数值分析、CUPID和NEMO程序等方法计算过,其原理为质子产生的所有反冲原子能量Lindhard分离函数部分总和的均值[2–3]。
Geant4是欧洲核子中心开发的的蒙特卡洛模拟软件,可应用于空间辐射损伤效应分析等方面,其强大的空间建模能力和精细的物理模型,对于空间辐射环境半导体元器件损伤效应分析,可同时模拟质子的屏蔽和损伤效应,减少了计算误差。
本文用Geant4模拟质子在半导体硅中的NIEL值与入射质子能量的关系。
1 NIEL值计算
由质子与Si的相互作用过程可知,反冲原子的源为卢瑟福散射晶格原子(<10 MeV)、核弹性/非弹性碰撞产生的Si晶格原子和核反应产物。
反冲核动能 T可分为两部分,一部分引起 Si材料的位移损伤,另一部分引起进一步的电离或激发。位移损伤的部分为反冲原子能量T的Lindhard分离函数Q部分,Q为反冲原子能量T的函数,其值为反冲原子通过弹性和非弹性碰撞损失的能量。1963年,Lindhard等[4]引入近似输运动力学方程,弹性过程能量损失计算用Thomas-Fermi势。
由此推导 NIEL(单位:MeV·cm2·g-1)值 SNIEL为:
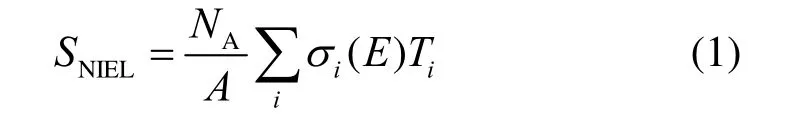
其中,si为i反应截面,Ti为i反冲原子平均能量位移能量损失部分(Lindhard分离函数),NA为阿佛加德罗常数,A为靶原子的质量数。
1968年,Robinson修正了Lindhard函数,分离函数Q可表示为:
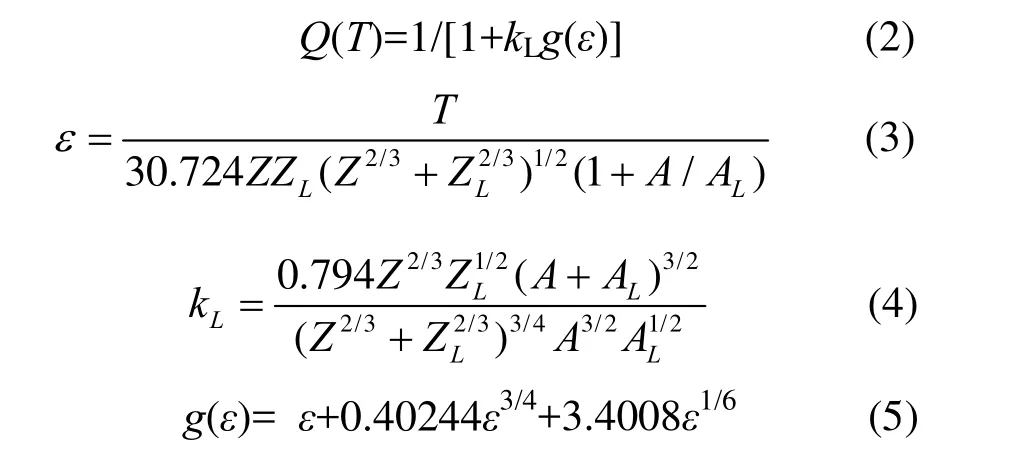
其中,T是反冲原子能量(keV), Z和ZL分别为晶格原子序数和反冲原子序数,A和AL分别为晶格原子质量(amu)和反冲原子质量(amu)。
式(5)适用于反冲原子类型为Si、能量较高的离子,若 E0<0.01 MeV/amu,式(5)的精确度不高。Akkerman等[5–6]修正了200 keV以下的反冲原子能量分离函数,计算结果与更精细的分子动力学计算结果相吻合,并给出了Q函数的表达式,适用于Z≤15的反冲原子,即式(5)的g(ε)由式(6)代替:
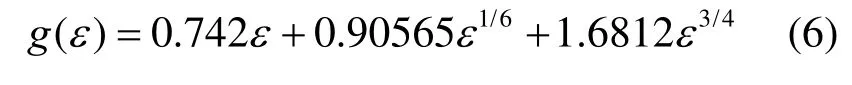
一般说来,质子能量大于300MeV宜用式(5),质子能量小于100 MeV宜用式(6),质子能量介于两者间,可根据反冲原子能量大于或小于 200keV分别取式(5)或(6)。
基于上述计算原理,忽略Rutherford散射初级撞击原子(primary knock-on atom,PKA)贡献,可知本文计算的 NIEL值实际上为质子与核弹性、非弹性碰撞和核反应过程中产生的反冲原子Q部分能量和的均值。
2 程序设计
2.1 GEANT4模拟物理模型[7]
在GEANT4中,粒子产生的物理过程归于电磁相互作用模块和强相互作用模块。电磁相互作用包括多次散射、电离、光电效应、轫致辐射等过程,使用的数据库文件基于 Livermore实验室的ENSDF、EEDL、EPDL97、EADL库;强相互作用包括弹性散射、非弹性散射和原子核嬗变。
程序中质子能谱屏蔽模拟采用 REMSIM 物理模块,半导体损伤模拟采用D H Wright (SLAC)编写的空间电子学物理模块,两者的差别在于对低能中子物理模型的处理不同,后者对低于20 MeV的中子采用基于 ENDF/B-VI反应截面文件的G4NDL3.11模块。弹性散射采用两体碰撞近似类G4LElastic(重荷除外);质子、中子非弹性散射和核嬗变采用Bertini(19.9MeV – 9.9GeV)、LEP(9.5GeV–25GeV)和 QGSP(15GeV–100TeV)三个能量段互补模型;氘、氚、3He、a和重荷粒子的非弹性作用采用类G4BinaryLightIonReaction;电离作用氘、氚采用类G4hIonisation,3He、a和重荷采用类G4ionIonisation。
2.2 模型设计
Geant4模拟的几何模型采用薄靶近似,即相对于不同能量的入射质子,几何(长方体)厚度 h为质子射程的1/10–1/100,长/宽比为几何厚度的10倍,反冲原子产生率较低,故薄靶要足够厚,以使质子发生核作用的几率能抵消随机性误差,生成足够多的反冲原子;反冲原子反冲核Q分离函数中,g(ε)按§2.1说明取(5)或(6);次级粒子阈值为0.01 mm,模拟的质子数为104–5×105,取决于薄靶对于质子射程的相对厚度。NIEL值由式(1)推导为:

其中,h(cm)为薄靶的厚度,Ed(MeV)为薄靶内沉积的位移损失能量,ρ(g/cm3)为半导体Si的密度。
3 结果与讨论
表1为Geant4模拟入射质子能量关系的参数和NIEL模拟值。
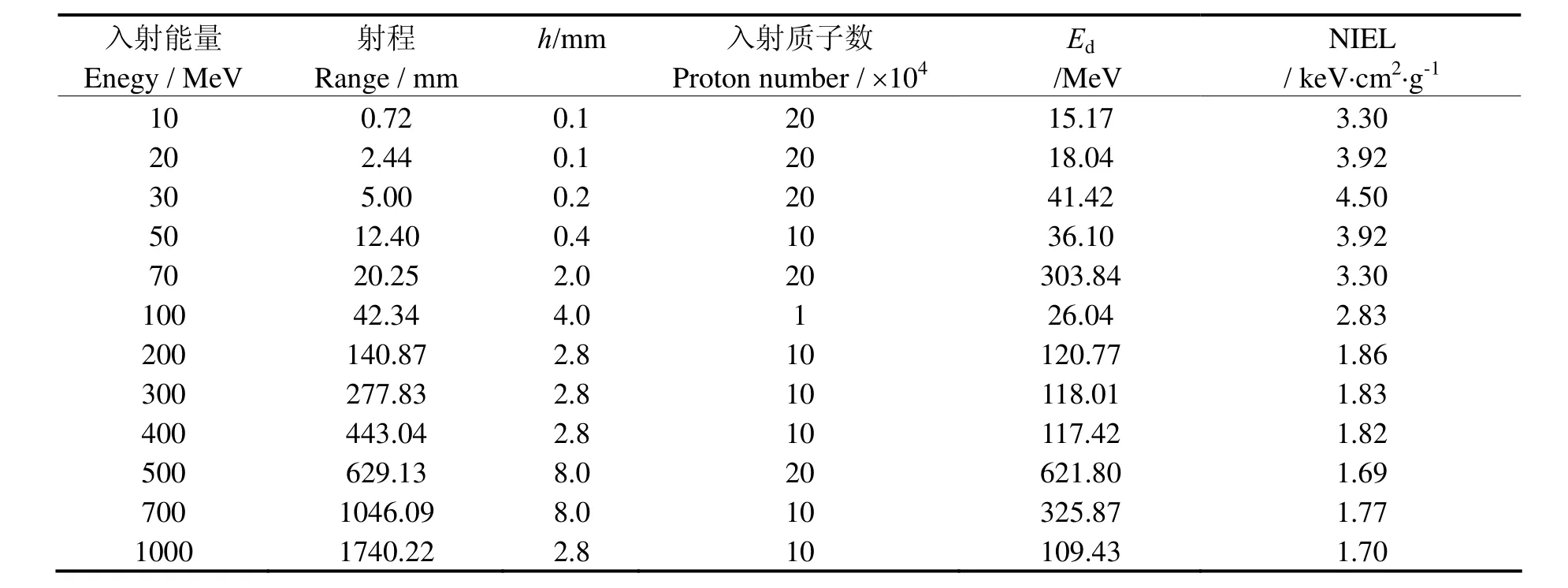
表1 Geant4模拟相关参数和NIEL值结果Table 1 Parameters of Geant4 simulation and NIEL results.
图1为本文的 Geant4模拟值与 Jun等[8]和Summers/Burke等[2]的计算结果的比较,插图为10 MeV–1 GeV能量范围的放大,可见在10 MeV –1 GeV能量范围内,本文用Geant4模拟核相互作用NIEL值是精确的。
对于入射能量范围为10MeV–1GeV的质子,本文的NIEL模拟值和文献[2]、[8]有一定的差别,其原因可分析如下:
(1) 质子能量小于30 MeV时,NIEL值模拟结果和文献[2]、[8]相差较大,主要原因是:此能量范围内,库仑散射在薄靶内位移能量损失贡献最大,而由模拟物理过程可知,Geant4类G4MultipleScattering在处理库仑散射的过程中不生成次级反冲晶格原子,因此,忽略库仑散射项的贡献,导致Geant4模拟NIEL结果在此能量范围偏小;此外,模拟的几何厚度较小,反应概率偏小,产生的反冲原子数目随机性较大,也影响了计算结果的精确度。

图1 Geant4模拟NIEL值与Jun等[8]和Summers/Burke等[2]结果的比较Fig.1 Comparison between NIEL results by Geant4 and by Jun et al.[8] and Summers/Burke et al.[2]
(2) 质子能量大于30 MeV时,NIEL值模拟的结果介于文献[2]、[8]的结果之间,且更接近于文献[2]的值。由文献[2]、[8],Summers/Burke的值为质子与Si核弹性与非弹性NIEL值的和,与本文模拟所考虑的物理过程相同,因此,上述能量范围内本文的模拟结果可靠。
(3) 质子能量大于 200MeV时,Jun值比本文和Summers/Burke小,主要原因可能是采用的物理模型不同:对 NIEL值贡献较大的高 Z(Na、Mg、Al、Si等)反冲原子平均能量差异较大。
4 小结
本文根据入射质子和生成的反冲原子能量大小,采取分段位移能量分离函数,基于Geant4编程对半导体物质的NIEL值进行了模拟,模拟结果为质子与核弹性、非弹性碰撞和核反应过程中产生的反冲原子Q部分能量和的均值,和文献吻合较好。因此,空间辐射经过屏蔽后的器件损伤效应分析,基于Geant4模拟提供了一种有效的途径。
1 Srour J R, McGarrity J M.Radiation effects on microelectronics in space [J].Proceeding of the IEEE Trans Nucl Sci, 1988, 76(11): 1443–1469
2 Dale C J, Chen L, McNulty P J, et al.A comparison of monte carlo and analytic treatments of displacement damage in Si microvolumes [J].IEEE Trans Nucl Sci,1994,41(6), 1974–1983
3 Inguimbert C, Gigante R..NEMO: A code to compute NIEL of protons, neutrons, electrons, and heavy ions.IEEE Trans [J].Nucl Sci, 2006, 53(4): 1967–1972
4 Srour J R, Marshall C J, Marshall P W.Review of displacement damage effects in silicon devices [J].IEEE Trans Nucl Sci, 2003,41(6): 653–670
5 Akkerman A, Barak J, Chadwick M B, et al.Updated NIEL calculations for estimating the damage induced by particles and gamma-rays in Si and GaAs [J].Radiation Physics and Chemistry, 2001, 62: 301–310
6 Akkerman A, Barak J.Partitioning to elastic and inelastic processes of the energy eeposited by low energy ions in silicon detectors [J].Nucl Instru Meth, 2007, B260: 529–536
7 http://www.slac.stanford.edu/comp/physics/geant4/slac_physics_lists/micro/space_elect_physics_list.html [OL]
8 Jun I, Xapsos M A, Messenger S R, et al.Proton nonionzing energy loss (NIEL) for device applications [J].IEEE Trans Nucl Sci, 2003, 50(6): 1924–1928
