基于抖动的高速真随机数发生器的设计和实现
2011-03-24张鸿飞罗春丽姚志明
张鸿飞 王 坚 罗春丽 崔 珂 姚志明 梁 昊 金 革
(中国科学技术大学近代物理系 安徽省物理电子学重点实验室 核探测与核电子学国家重点实验室 合肥 230026)
随机数应用于许多场合,如计算机仿真算法、计算机游戏、统计学等,在密码学的各种应用的中,随机数更是必不可少。在这些应用中,很多算法和协议依赖于随机数来产生不可预测的安全密钥,因此需要高质量的随机数来保证系统的安全。比如在量子密钥分配的各种实现方案中,随机数在密钥的形成过程中起着至关重要的作用,如果这些随机数被第三方窃取或破解,通讯双方通过公共信道讨论探测结果时,窃听者可能完全获取密钥而不被发现。因此,无论是在经典的信息安全领域还是在量子信息领域,都须有一个真随机数发生器(True Random Number Generator, TRNG)。
1 真随机数产生方法
目前有很多办法产生各种真随机数,比如利用混沌系统[1],利用噪声ADC采样[2],利用光的量子效应[3]等,本文设计的随机数发生器是利用电子元件的噪声引起的数字逻辑中的随机晃动(jitter)来产生的。最常见的基于数字电路的真随机数产生方法为:
1.直接放大法[2,4]:放大电路中的电阻热噪声等物理噪声,通过比较器比较以获得随机数序列。
2.振荡采样法[5–9]:通过D触发器把两个独立的振荡信号进行数字混合,用低频信号采样高频信号,利用环形振荡器的频率抖动作为随机源,并进行后处理,从而得到随机数序列。
3.离散时间混沌法[1,10,13]:利用混沌电路不可预测行以及对初始条件敏感的依赖性产生随机数。
4.亚稳态采样法[14-16]:利用数字电路的亚稳态作为随机源。亚稳态是指触发器无法在某个规定时间段内达到一个可确认的状态,比如在同步系统中,若触发器的建立时间/保持时间不满足,就可能产生亚稳态。触发器输出端Q在有效时钟沿后较长的一段时间处于不确定的状态,这种不确定状态最终会在Q端随机输出0或1,与输入并无必然联系,从而得到随机序列。
如图 1所示,影响 TRNG性能者有:熵源(Entropy Source),采集手段(Harvesting Mechanism),以及后处理(Post-processing)。

图1 真随机数发生器的一般框图Fig.1 Diagram of a true random number generator.
基于模拟电路的结构,有直接放大法和离散事件混沌法。直接放大法真随机数发生器的熵源的统计分布更为理想,且熵源噪声不随采样周期变化,但由于采用模拟电路,其依赖于集成电路工艺,且资源消耗大。
基于数字电路的结构,有振荡采样法和亚稳态采样法。对于亚稳态采样法,由于数字电路中的亚稳态时间较短,且对温度和电压的变化非常敏感,因此利用亚稳态获得的随机数一般速率都很慢,且很难做到稳定,于是更多地使用震荡采样法。
振荡采样法真随机数发生器的功耗较低,集成度较高,便于在通用可编程平台(如FPGA、CPLD)上实现,且易于在SoC中使用。本设计所用的真随机数产生方法基本思想是震荡采样法。
本文用在FPGA内部产生的震荡环的抖动作为随机源,通过二次采样来改善随机数的随机性和输出的稳定性,采用基于LFSR(Linear Feedback Shift Register)的后处理,以很小的硬件代价改善了随机数的统计特性,从而以较低的成本得到高性能、高速率的真随机数。
2 真随机数的设计
对应于图 1,本设计按三个部分来说明:随机数源、随机数采集模块和后处理模块。
2.1 随机源模块及Jitter
数字电路中的时钟信号总有抖动现象,如图2所示。随机抖动的来源为热噪声、散粒噪声和低频噪声(1/f噪声),与电子器件和半导体器件的电子-空穴特性有关,因此我们讨论的是抖动是随机抖动,其分布是平均值为0、满足高斯分布的随机变量[17]。时钟的抖动适合于在数字电路中作为真随机数发生器的噪声源,而是否能准确有效提取这种随机信号是设计TRNG的关键。

图2 时钟的晃动示意图YFig.2 Jitter of a clock.
我们在FPGA 内部使用2 N + 1 个反相器组成一个闭合的环路(或N个buffer加一个反向器)得到高频振荡时钟。该时钟信号的周期与门延时及反相器的个数有关,而与外部信号无关。这种完全由反相器构成的环路功耗较大,需在环路中加入一个使能(图3),无需随机数生成器工作便可关闭振荡环,以降低系统功耗。

图3 震荡环的示意图Fig.3 Structure of an oscillator ring.
振荡环的输出不可避免地存在时钟抖动(图2),相比于用PLL或DLL等采取反抖动措施产生的时钟,其具有更大的抖动,便于采样模块的抖动采样。
2.2 前端采样
根据上述分析,需把振荡环的这种抖动有效的提取为随机数的输出,我们采用2次采样法。
首先用两个频率很接近的振荡环,一个振荡环对另一个振荡环进行采样,如图4(a)所示;其相应的采样时序如图4(b)所示,两振荡环在上升沿重叠的区域形成采样的随机性,造成在重叠区域的前后2个时钟,使C的输出可能是0也可能是1,从而得到一次采样的一路随机数。
整个采样模块如图5所示,先生产n个振荡环,这些振荡环由同样数目的反向器组成,并且通过手工布线,使这n个振荡器的频率差异细微。取其中一个振荡环作为采样时钟,去采样其他n−1个振荡环。采样功能由子采样模块(图4a)完成。通过这样的采样,得到n−1组数据,这n−1组数同时进入一个异或操作,再通过一个采样时钟FS进行二次采样,得到原始的随机数。
对于一次采样后的信号,由于使用同样的采样时钟,其跳变沿相互接近,则对上升沿-上升沿叠加或上升沿-下降沿重合进行异或而得到的随机信号序列(图6),均包含了新的采样后的随机性,提高了整个序列的随机性。但由于一次采样中存在一个时钟的偏差,在一次采样后的跳变沿不一定全都接近,同样会有一个时钟的偏差,会引入确定性偏差而导致随机数输出的偏置,这须由后处理来进行纠偏。
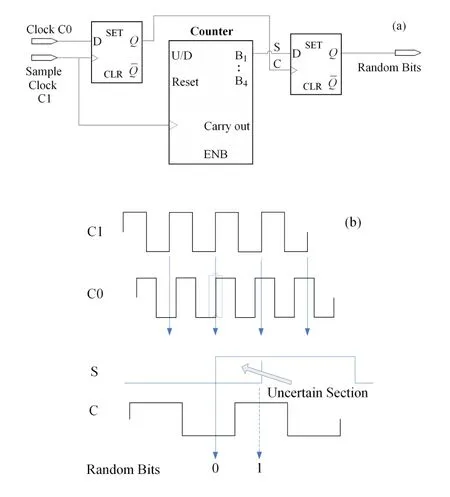
图4 一次采样框图与采样时序Fig.4 Diagrams of the first sampling and its timing sequence.

图5 采样模块框图Fig.5 Structure of the sampling module.
2.3 后处理模块
理想情况下,二次采样所得信号具有随机的统计特性。由于芯片会受温度电压等的影响,这导致采样过程中出现偏置,影响结果的统计特性;而采样的DFF可能出现亚稳态,影响信号的偏置。我们可通过二级锁存来减少亚稳态的出现,但是温度电压等的影响始终存在,则通过上一步骤产生的原始随机数会有偏置(bias),须进行削偏后处理。
本设计采用基于线性反馈移位寄存器(LFSR)的XOR后处理,如图7所示。通过对11位移位寄存器进行抽头异或而得到,不同的抽头会得到不同的纠偏效果。原始随机数序列从随机序列端输入,同时给一个采样时钟,通过纠偏处理之后的数据通过随机数输出端输出,得到最终得到的随机数序列。在实验中,采用1、4、5、7、8、9之后进行抽头异或,可以得到比较好的结果。

图7 基于LFSR的后处理示意图Fig.7 LFSR-based post processing.
3 基于FPGA的实现
FPGA具有可重构性且性价比高,本随机数发生器具有集成灵活性,可很方便地与FPGA中的其他功能进行集成;也可根据需要,在FPGA的资源范围内,任意添加所需随机数产生器的路数;接口灵活,可很方便地设计各种硬接口和软接口,以满足各种应用的需求。
本设计采用USB技术实现对PC的接口,使产生的高速随机数流能很方便地与其他高速应用结合,同时也提供了其他接口,如 RS232、RS485、自定义总线等。其硬件框图如图8所示,所用FPGA为Altera公司的Cyclone III,当然此设计也可在其他FPGA上实现。

图8 随机数产生器的硬件框图Fig.8 Hardware of the TRNG.
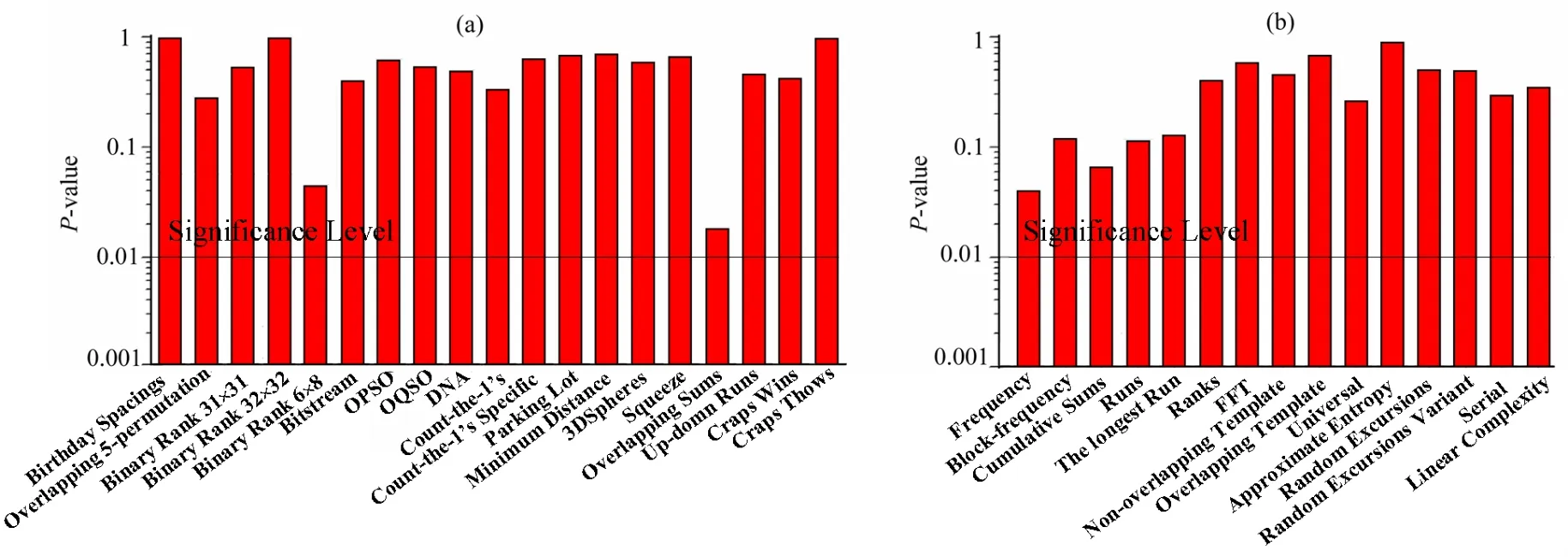
图9 随机数的测试结果 (a) NIST测试结果,(b)Diehard测试结果Fig.9 Test results of TRNG.(a) random test result of NIST, (b) random test result of Diehard.
在此硬件平台进行一系列的试验,产生的随机数通过USB上传到PC机上进行随机性分析,主要采用美国国家标准和技术研究所(NIST)提供的随机数测试程序 STS[18]和由 George Marsag编写的Diehard测试程序[19]进行测试。在单路一次采样的实验基础上进行了二次采样的实验,在反向器个数为11个,周期为6.7ns左右(~150 MHz),子采样数为4个的情况下,通过改变二次采样的频率,分别在 1、2、4、8,16、24、28、32、50 MHz 的频率下进行采样,采样数据为500 Mb。在频率低于20 MHz的数据均能通过 NIST测试,如图 9所示是20M采样时钟下的测试结果。
一个单路输出的TRNG,有5个振荡环路,每个振荡环路有11个反相器,共有59个LUT和20个Register,全部的LE使用71个,加上USB接口,FPGA的逻辑资源仅使用317个LE。单路使用了非常少的资源,因此很容易在FPGA中集成几十路、上百路的随机数产生器,可使整个FPGA获得相当高的随机数产生速率。
4 小结
基于以上设计和实验,完成了一个基于振荡环抖动的真随机数产生器,速率达到20 Mbps,并通过了NIST测试程序的测试以及Diehard测试程序的测试。本设计不需要特殊的资源(如 PLL),占用资源非常少(小于 100个逻辑单元),可在任何 FPGA中实现。
1 Miloˇs Drutarovsk´y, Pavol Galajda, Chaos-based true random number generator embedded in a mixed-signal reconfigurable hardware [J], Journal of Electrical Engineering, 2006, 57(4): 218–225
2 Holman W T, Connelly J A, Dowlatabadi A, An integrated analog/digital random noise source [J], IEEE Trans.Circuits Syst.I, 1997,44(5):469
3 Dynes J F, Yuan Z L, Sharpe A W, et al.A High Speed,Post-Processing Free, Quantum Random Number Generator [J], Applied Physics Letters, 2008, 93(3),031109 - 031109-3
4 Petrie Craig S, Connelly J.Alvin, A Noise-Based IC Random Number Generator for Applications in Cryptography [J], IEEE Transactions on Circuits and Systems—I: Fundamental Theory and Applications, 2000,47(5):615–621
5 Sunar B, Martin W J, Stinson D R, A provably secure true random number generator with built-in tolerance to active attacks [J], IEEE Transactions on Computers, 2007, 56(1):109–119
6 Knut Wold, Chik How Tan, Analysis and enhancement of random number generator in FPGA based on oscillator rings [C], International Conference on Reconfigurable Computing and FPGAs, Dec.2008, Cancun, Mexico
7 Alioto M, Fondelli L, Rocchi S.Analysis and performance evaluation of area-efficient true random bit generators on FPGAs, 2008 International Symposium on Circuits and Systems, May 2008, Seattle, USA
8 Schellekens Dries, Preneel Bart, Verbauwhede Ingrid.FPGA vendor agnostic true random number generator[C],International Conference on Field Programmable Logic and Applications, Aug.2006, Madrid, Spain.
9 Kohlbrenner Paul, Gaj Kris.An Embedded True Random Number Generator for FPGAs[C], Proceedings of the 2004 ACM/SIGDA 12thinternational symposium on Field programmable gate arrays, Feb.2004, Monterey, CA, USA
10 Utarovsky'Milos D R, Galajdai Pavol.A robust chaosbased true random number generator embedded in reconfigurable switched-capacitor hardware [C], The 17thinternational Conference on Radioelektronika, April 2007,Brno, Czech Republic.
11 Viktor Fischer, Milos Drutarovský, True random number generator embedded in reconfigurable hardware [C],Proceedings of CHES 2002, the4thInternational Workshop on Cryptographic Hardware and Embedded Systems.
12 Kwok S H M, Lam E Y.FPGA-based high-speed true random number generator for cryptographic application[C], TENCON 2006.2006 IEEE Region 10 Conference,Nov.2006.
13 Gerosa A, Bernardini R, Pietri S.A fully integrated 8-bit,20 MHZ, truly random numbers generator, based on a chaotic system mixed-signal design [C], 2001 Southwest Symposium on Circuits and Systems.
14 Epstein M, Hars L, Krasinski R, et al.Design and implementation of a true random number generator based on digital circuit artifacts [J], Lecture Notes in Computer Science, 2003, 2779/2003: 152–165
15 Kinniment D J, Chester E G., Design of an on-chip random number generator using metastability [C],Proceedings of the 28thEuropean Conference on Solid-state Circuits, Sept.2002, Firenze, Italy.
16 Danger J L, Guilley S, Hoogvorst P.Fast True Random Generator in FPGAs [C], Proceedings of 2007 IEEE Northeast Workshop on Circuits and Systems, 506–509
17 John A.McNeill, Jitter in Ring Oscillators, IEEE Journal of solid-state circuits, 1997, 32(6):276
18 NIST.NIST Random Number Generation and Testing[OL], 2010, http://csrc.nist.gov/rng
19 Diehard, 1996, http://en.wikipedia.org/wiki/Diehard_tests[OL]
