中子导管输运特性的数值计算方法
2011-03-24李新喜黄朝强
王 燕 李新喜 黄朝强 陈 波
(中国工程物理研究院核物理与化学研究所,绵阳 621900)
中子已广泛地应用于材料科学以及基础科学研究中,中子导管则广泛地应用于反应堆上,以传输和过滤中子[1–3]。中子的输运特性,是中子光学设备理论设计和优化的一个重要方面。常用的中子输运模拟计算程序有Mcstas[4]与Vitess[5],系Mont Carlo法的中子输运软件,可从网上下载获得。Pusenkov等[1]介绍了他们的数值计算软件的优越性,相对于Mcstas和Vitess软件,数值计算方法能精确计算中子轨迹,尤宜应用于有缺陷的中子光学输运设备。而许多中子光学设备并非十分理想,Mcstas和Vitess软件难以避免产生输入误差。我们基于C++控制台应用程序编写了数值计算程序NCMP,本文利用该程序计算了两个中子导管的中子输运特性,通过分析和比较,为获得程序的计算误差及可能的进一步开发提供参考依据。
1 基本原理
中子导管数值模拟计算中,导管出口注量率可表示为:

式中,T(l)是中子导管的透射系数(Mean accepted divergence)[1],对于矩形中子导管,

式中,H(l)和V(l)分别是横向和纵向的透射系数,
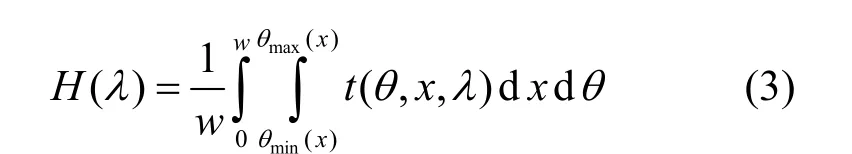

式(3)中,θmin(x) ≤ θ ≤ θmax(x), 0 ≤ x ≤ w; 式(4)中,θmin(y) ≤ θ ≤ θmax(y), 0 ≤ y ≤ h。每个中子的波长lm以及其在导管入口坐标xj和飞行角度qi决定其到达出口的可能性,即

式中,R(4παn/lm)为相应波长的反射率,N为中子在导管内的反射次数,an为第n次反射时的掠入射角。
2 结果与讨论
2.1 理想多道弯导管模拟计算
为得到更好的几何近似,采用了弯曲部分的切分近似,中子导管被分成很多短的、直的部分。短者的高和宽在出入口有所不同,第k段的示意描述见图1。图中,是入口和出口参数,Φwk和Δwk为角度与尺寸的偏差,玻璃基底的厚度为δk。
计算采用Maxwell波长分布无穷大面源FM(λ)=2F0(lT)4l–5e–lT/l,积分通量 F0=1.4×1013n·cm–2·s–1,特征波长lT= 0.168 nm。多道弯导管超镜因子m=2,全反射率为 1(理想情况)。导管在横向上(x方向)弯曲,多道也在横向上排列。弯曲中子导管相关导管参数见表1。

表1 计算采用的主要输入参数Table 1 The main input parameters for calculation
图2给出了NCMP计算的结果(与文献[1]的结果一致)。对短波长的中子(<0.1 nm),横向透射系数基本为 0,即弯导管对短波长中子的过滤很好。对于长波长中子,波长越大,透射系数也越大,因为长波长中子的全反射临界角大。图2表明,波长大于0.2nm的中子的透射系数与波长基本成线性关系,这是因为计算时把中子在导管中的反射小于临界角的反射率都假设成 1,而大于临界角反射率为0。
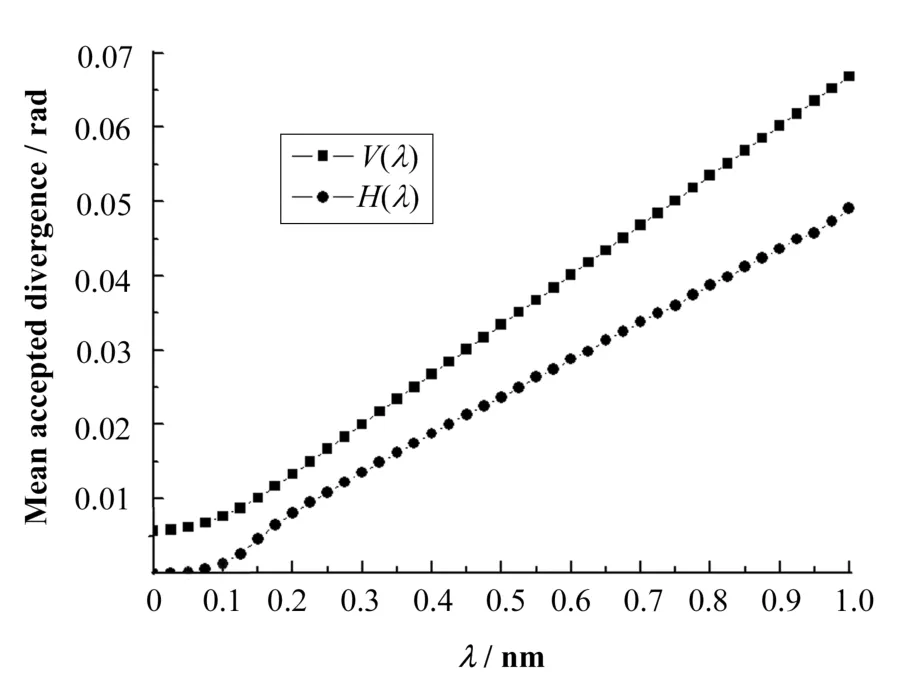
图2 NCMP计算弯导管纵向和横向透射系数Fig.2 The mean accepted divergence of guide C3 calculated by NCMP.
由式(4)、(5),长波长中子纵向透射系数与波长线性关系可近似为:

式中的系数kni= 0.0173 rad/nm为天然镍的中子全反射临界角与波长比[6],m为超镜因子。
对长波长中子的横向透射系数,由于多道的影响,须在式(6)中乘一个因子G,G为导管入口中子通过截面积与去掉多道后的总截面积之比,即
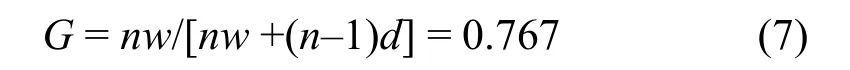
式中参数见表1。则长波长横向透射系数可近似为:

式(6)、(7)、(8)是在反射率设为1的理想情况下,实际的导管反射率并非如此,故需用数值模拟。
2.2 冷中子导管C3的模拟计算
上文中,将理想导管全反射率假设为 1,但实际的导管不会如此理想。C3导管的反射率模型为:

式中q为动量转移,m为导管超镜因子,rmax、rmin分别为导管反射率最大值以及截断处反射率。
从慢化剂出来的中子源可看作是面源,面源尺寸90 mm(W)×200 mm(H)。其理论中子能谱由俄罗斯圣彼得堡核物理研究所的Pusenkov教授提供,如图3所示。
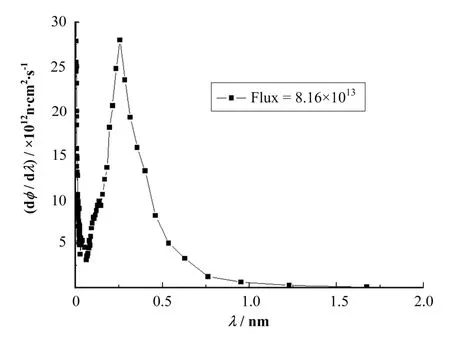
图3 中子注量率计算中使用的液氢冷中子源初始谱Fig.3 The energy spectrum of liquid hydrogen moderator in calculation.
中子导管长1.6 m的直导管入口与慢化剂的距离为2.295 m,接长度为13.45 m、曲率半径为556m的弯中子导管,再接长度为31.45m的中子直导管。整个导管系统超镜因子均为 m=1.5,导管光学截面均为 30mm(W)×200mm(H)。表 2是计算程序所用到的C3导管系统参数,其中导管表面弯曲度以及单段导管间隔厚度精度是本数值模拟程序为了更准确模拟导管所用到的特色参数[1]。

表2 C3导管的输入参数表Table 2 The main input parameters of C3 neutron guide for calculation
图4给出了对C3冷中子导管出口注量率的计算比较结果,从图中可以看出,利用NCMP计算得到的结果与 Pusenkov教授提供的计算结果基本上一致,偏差的引起可能是弯曲导管的分段数与Pusenkov所用分段数不一致以及精度步长不同,导致对弯曲部分导管的计算精度不一致。从中子注量率的结果来看,差距非常小。
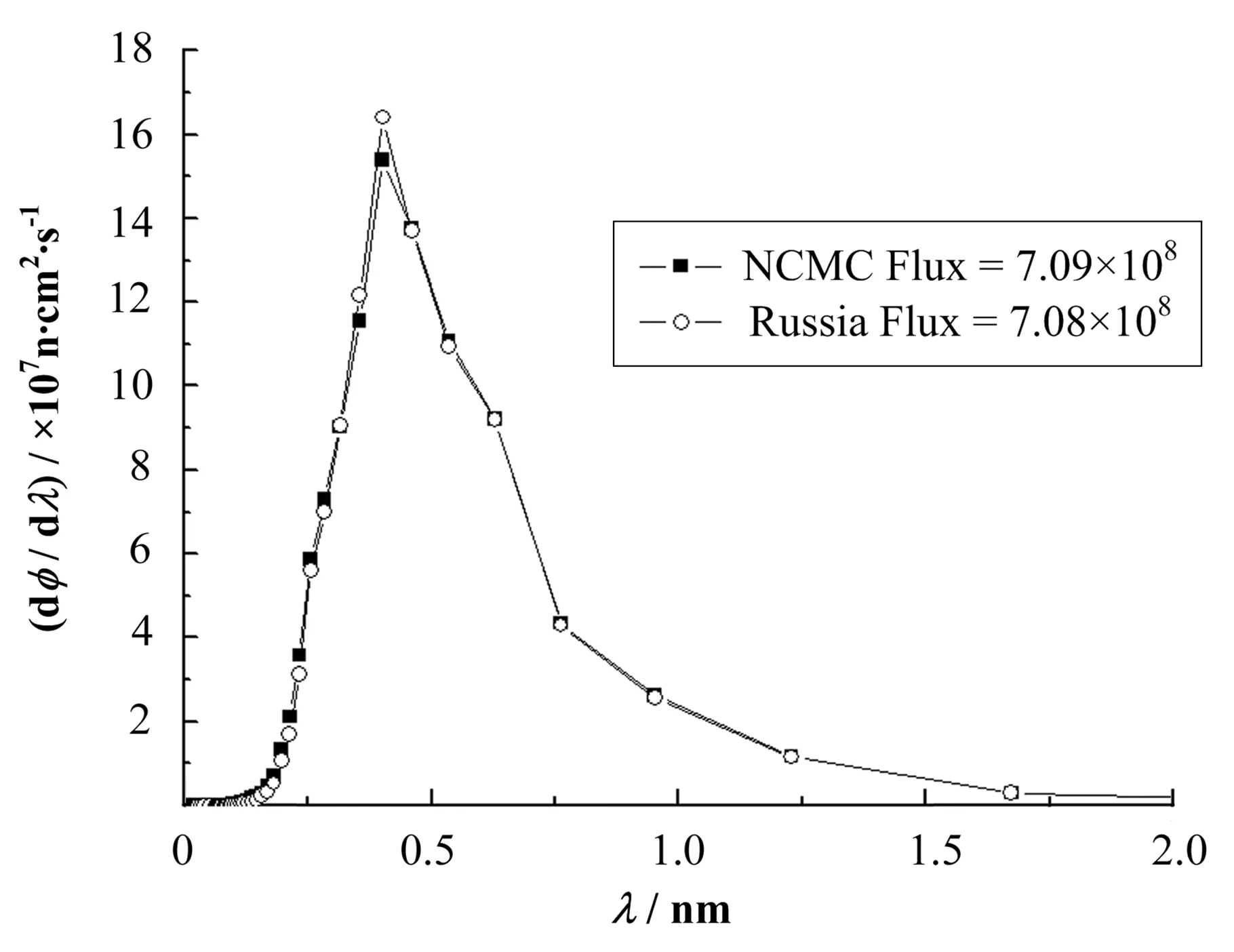
图4 出口注量率与俄罗斯Pusenkov教授提供的计算结果比较Fig.4 Comparion between the calculated flux by Professor V.M.Pusenkov and NCMP.
C3冷中子导管的透射系数与中子波长的函数关系见图5,可见中子导管对波长大于0.25nm中子具有良好的中子传输性能,能较好地完成冷中子的输运,对短波长中子则能很好地过滤。

图5 NCMP 计算的C3导管透射系数与波长关系曲线Fig 5 The mean accepted divergence in XY plane and index calculated by NCMP.
中子在中子导管内的输运性能,与中子在 XY平面内的发散密切有关。XY平面内的发散影响中子通量的大小,对于带有一定准直功能的多道中子导管,导管输出 XY平面内的发散情况也反映了中子导管的中子输运特性。C3冷中子导管XY平面内的发散情况计算结果见图6。
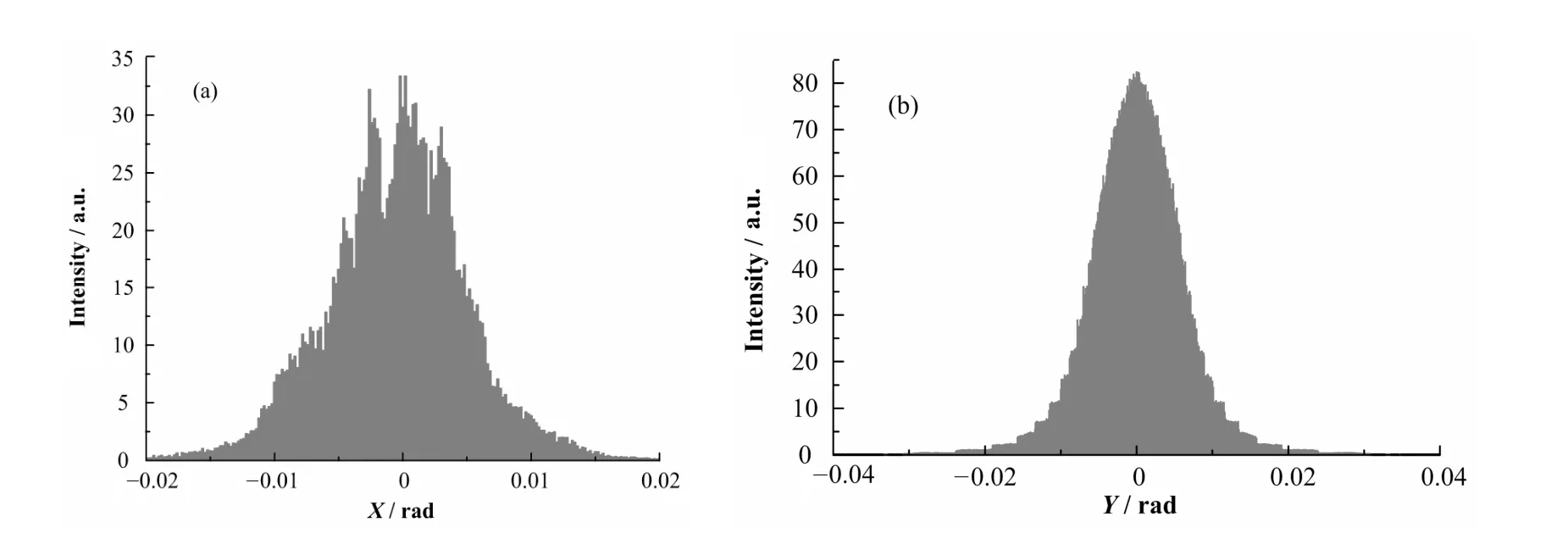
图6 NCMP计算的横向和纵向发散情况(X,横向;Y,纵向)Fig.6 The divergence in X-Y plane calculated by NCMP.
图7给出的是俄罗斯Pusenkov教授的计算结果,图6的发散情况与之基本相同,仅在图形的光滑度上略有差别,这可能是由于计算采用的精度步长不同所致。

图7 Pusenkov教授提供的横向和纵向发散情况(X,横向;Y,纵向)Fig.7 The calculation result of divergences in X-Y plane supplied by Professor V.M.Pusenkov.
综上所述,我们用自行编写的数值计算程序NCMP计算了两个中子导管模型、理想的多道弯导管以及俄罗斯Pusenkov教授提供的冷中子导管C3。
对于理想的多道弯导管,计算结果与文献[1]中提供的透射系数以及理论分析完全相符。
对于冷中子导管 C3,本文计算结果与文献[1]基本上吻合(图4),仅由于模拟计算所采用的精确度不同而略有差异。对于源与C3导管组成的整个系统的透射系数,Pusenkov教授未提供相应的计算输入参数,无法将NCMP程序计算结果(图5)作对比;但由图4中的注量率计算结果,用NCMP软件计算的XY平面内可接受的发散及透射系数是准确的,可供导管优化或导管后谱仪优化的输入特性计算作参考。
3 结论
本文介绍了 NCMP数值计算方法模拟程序基本原理和相关计算,并与文献[1]以及 Pusenkov教授提供的计算结果作比较,结果表明该程序可以进行准确的中子输运特性模拟计算。由于数值计算方法的灵活性和准确性,针对一些有缺陷的中子光学输运设备,通过模型上的处理和修正,能够获得更为精确的计算结果。因此,该程序可为中子光学输运设备的理论模拟计算提供更多的选择,为相应的中子光学设备理论设计或优化提供参考。
1 Pusenkov V M, Schebetov A, Gibcus H P M, et al.Numerical calculation of neutron fluxes at the exit of a complex neutron-guide system at IRI, Delft [J].Nucl Instr Meth, 2002, A492: 105–116
2 van Well A A, de Haan V O.The average number of reflections in a curved neutron guide [J], Nucl Instr Meth,1991, A309: 284–286
3 Mildner D F R, Chen-Mayer H H, Lamaze G P, et al.Characterization of a cold neutron beam from a curved guide [J].Nucl Instr Meth, 1998, A413: 341–351
4 http://www.mcstas.org.2008 [OL]
5 http://www.hmi.de/projects/vitess, 2008 [OL]
6 丁大钊, 叶春堂, 赵志祥, 等.中子物理学[M].北京:原子能出版社, 2005 DING Dazhao, YE Chuntang, ZHAO Zhixiang, et al.Neutron Physics [M].Beijing: Atomic Energy Press, 2005
