利用飞参数据实现飞机机体结构寿命的动态监控

贺 漫，杨晓华

（1.海军驻青岛地区配套设备军事代表室，山东 青岛 266042；2.海军航空工程学院青岛分院，山东 青岛 266041）

航空维修要实现从现行的反应式、基于故障维修向基于状态维修计划的转型，就需要减少甚至取消依靠假设的疲劳寿命或标准化的大修时间安排的定时维修任务。

从强度的观点看，[1]飞机设计经历了从静强度、静动强度、疲劳强度、损伤容限及可靠性设计等5个阶段；从设计原理来看，损伤容限及可靠性设计比较符合基于状态维修的思想。但目前国内引进的或自制的直升机在给出机体结构寿命指标值时，按照的依旧是疲劳强度的设计原理。维修模式转为状态维修后，如何确定机体结构当前状态的可靠度和翻修的时间便成为亟待解决的问题。[2-3]本文通过对某型直升机重心法向过载飞参数据的研究，力图为飞机机体结构按状态维修提供理论上的依据。

1 利用飞参数据实现飞机机体结构寿命的动态监控

利用飞参数据实现飞机机体结构寿命的动态监控的步骤如下：[4]

1）获取飞参数据，并将其转换成可识别的工程量；

2）编制合理的载荷谱；

3）根据每架机的载荷谱选择合适的疲劳理论，分析计算机体结构的疲劳损伤和疲劳寿命；

4）根据计算得到的寿命，分析机群在指定寿命下的可靠度，并确定修理周期。

2 某型直升机机体结构寿命的动态监控

2.1 飞参数据的获取

直升机的飞参数据包括法向过载、剩余油量等20多个开关量，根据直升机机体结构疲劳损伤的特点，本文将直升机机体结构的状态定义为法向过载。

无论是引进机还是国产机其飞参数据均为模拟信号非数字信号。因此，可以依据每架飞机的参数校准表将所选的飞参参数的测量值转录成工程量，研制一个通用软件模块，根据所设的采样率（一般为8次/秒），将原始的机器码文件保存为标准的ASCII 码文件。

2.2 编制直升机的法向过载谱

图1为一段典型的由飞参数据转化得到的重心法向过载谱。为便于计算和试验，首先要对该谱进行统计计数处理。目前常用的计数方法有：限制穿级计数法、跨均峰值计数法、主峰值计数法、变程—均值计数法、变程对—均值计数法和“雨流”计数法等。

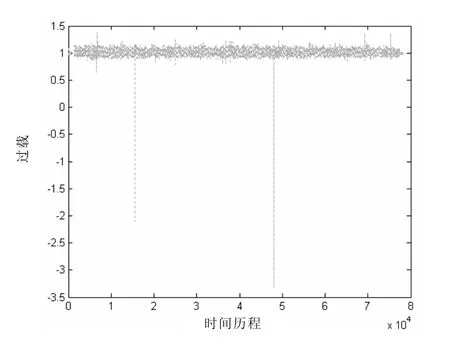
图1 原始的重心法向过载谱

“雨流”计数法被认为能够反映出材料在反复载荷作用下的应力应变响应的对应关系，所以其计数结果与材料应力—应变行为完全吻合，是疲劳界最通用的计数方法之一，本文采用“雨流”计数法。在雨流计数时结合直升机机体结构受力的特点作出如下的修正：[5]

1）噪声修正。计数时，当过载谱中出现连续增长或连续下降的数据点（小噪声），只取最大或最小的值，去除中间点。大量的飞参数据表明，直升机飞行过载的变化一般在0.1～0.25 范围内，个别达到0.5。在飞参记录中，存在一些独立的、突然出现的强烈变化的突峰，大者可达4 g，小者甚至到−3 g，这样过大和过小的过载对目前的飞行课目来说是不应该有的。

2）整体偏离的修正。个别过载谱整体上明显偏离过载为1的水平线，有的全部在1.1以上，这样的情况可能是由于过载传感器没有调校准确，使用这样的过载谱计算出的损伤要明显大于实际飞行形成的损伤，必须修正到1 附近。根据偏离程度做不同的修正，最大偏离0.3 g 及以上者可取原均值的1/10。

3）滤波，去除小幅值循环。一般认为直升机机体结构的疲劳属于高周疲劳，载荷谱中有数据巨大的小幅值循环，这些循环对结构的损伤影响较小，在工程计算中可以去掉，保留一定数量的大幅值循环（每1 000 h飞行出现累积数量在105次以内的过载）和均值远离总体均值的那些循环。

4）收敛、发散波的处理。按“雨流”计数法的法则，将滤波剩余的过载谱提取出过载循环，第一次计数后会剩余一个发散—收敛波，将该波从最大幅值处截断，前后对调后对接成一个收敛—发散波，在衔接处将首尾连接起来，这样的波形两端是自然“封闭”的，可以按照“雨流计数法”继续计数到最后一个循环被计入，完成第二次计数。

图2为按上述方法修正后的某型直升机重心过载谱片段。

图2 修正后的重心过载谱片段

2.3 疲劳损伤计算

直升机的机体结构一般是具有多路传力的静不定结构，承受飞行状态改变和地—空—地循环形成的低周疲劳载荷，但直升机机体结构的疲劳相对于固定翼飞机，其应力水平较低，可采用改进的疲劳损伤计算方法计算机体结构的疲劳寿命，而不必进行全尺寸结构的疲劳试验。为了利用重心过载谱进行疲劳损伤计算，本文发展了一种基于飞参数据的名义应力法进行损伤计算。

名义应力法是最早形成的抗疲劳设计方法，它以材料或零件的S-N曲线为基础，对照试件或结构疲劳危险部位的应力集中系数和名义应力，结合疲劳损伤累积理论，校核疲劳强度或计算疲劳寿命。名义应力法假定[6]：对于相同材料制成的任意构件，只要应力集中系数Kt相同，载荷谱相同，则它们的寿命相同。此法中名义应力和应力集中系数为控制参数。

名义应力法估算结构疲劳寿命的步骤为：

1）确定结构中的疲劳危险部位；

2）求出危险部位的名义应力和应力集中系数Kt；

3）根据载荷谱确定危险部位的名义应力谱；

4）应用插值法求出当前应力集中系数和应力水平下的S-N曲线，查S-N曲线；

5）应用疲劳损伤累积理论，求出危险部位的疲劳寿命。

这里，材料的S-N曲线是疲劳设计的基本数据资料，通过材料试件的疲劳试验获得的S-N曲线可在众多的手册资料中查得。根据直升机结构疲劳设计的工程特点和使用方便，文献对常用材料的S-N曲线试验数据重新进行归纳整理，给出全范围的材料S-N曲线如图3所示：[7]

图3 材料全范围的S-N曲线

直升机结构疲劳设计惯用的标准S-N曲线公式和参数（包括S-N曲线的形状参数A、α和位置参数疲劳极限∞σ）表示。

高周S-N曲线为：

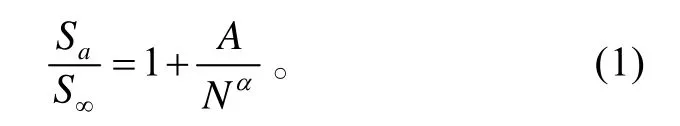
上式中的循环应力比为-1，A和α为材料常数，不妨采用LY12CZ的材料常数，A为0.4828，α为0.5。低周S-N曲线：材料屈服强度sσ和105处高周S-N曲线端点的连线。

平均应力修正采用古德曼修正：

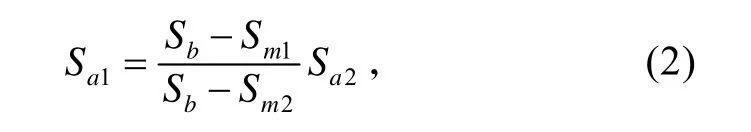
式中：Sa1为修正后（含平均载荷为S1m）的疲劳强度或交变载荷；S1m为修正后的平均载荷；Sa2为修正前的疲劳强度或交变载荷；Sm2为修正前平均载荷；Sb为结构的强度极限载荷。

对于引进的直升机在无原始设计资料数据的情况下，为了将过载谱转换成名义应力谱可以合理地假定直升机机体结构材料在所有情况下都不会进入塑性，因此过载谱中的一个当量过载循环 gdl对应S-N曲线中的应力 Si为：

这里S10n为当n=5时，S10n为S-N曲线中对应105次循环的应力值；当n=∞时，S10n为疲劳极限；gT为按要求截取过载循环的门槛值；gdl为当量过载循环，由下式定义：

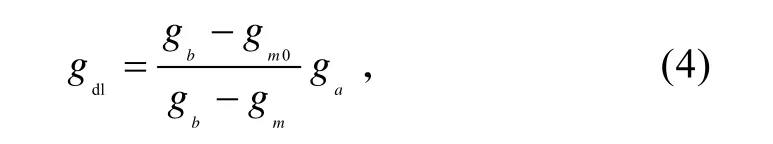
式中：gb为最大过载，这里取2；gm0为过载谱整体均值，这里取1；gmi为过载循环均值；gai为过载循环幅值。

有了 Si，从铝合金全范围S-N曲线可找到相对应的疲劳寿命值Ni，取倒数即为该循环的损伤Di=1/Ni。于是，整个过载谱的损伤为：

需要强调的是上述损伤值为相对损伤。

2.4 用相对损伤控制直升机的使用寿命

用上述方法计算了8架直升机飞行8 a 每架直升机飞行近1 000 h的相对损伤（若某架直升机飞行小时数不足1 000时，则可将其损伤按比例放大至1 000 h飞行）。计算结果表明3号机损伤最为严重，如果将3号机的相对损伤正则化为1，则其他7架机的损伤值如表1所示。可见3号机和1号机的相对损伤最为严重，飞行日志的分析表明这两架机经常用于飞行表演，超常规的机动飞行较多，损伤自然严重一些，这从一个侧面反映了上述方法的合理性。表1中出现一异常数据，6号机的相对损伤非常小，飞参检查表明其数据很不完整，该飞参记录仪需要重新调正。

表1 用基于飞参数据的名义应力法计算相对损伤

对引进机来说如供方给出的首翻期为1 000 h飞行，那么除相对损伤最为严重的3号机届时需进厂大修外，其余直升机均可延长使用。

2.5 机群寿命的可靠性分析

同以往寿命分析不同的是表1中的数据实际上是直升机无故障工作时间，即使是相对损伤最严重的3号直升机实际上还是可以正常飞行的。可假设直升机机体结构的疲劳寿命服从对数正态分布，即：

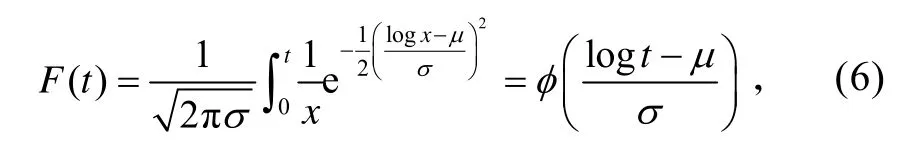
μ和σ为对数均值和标准差。在(1−α)置信水平下，可靠度 R (t)的最优单侧置信下限为：[8]

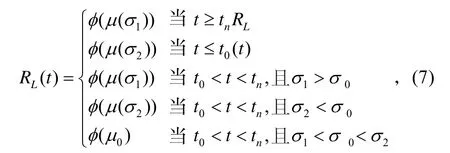
式中：tn=max(t1,t2,…,tn)，(μ0,σ0)是下列方程组的解：

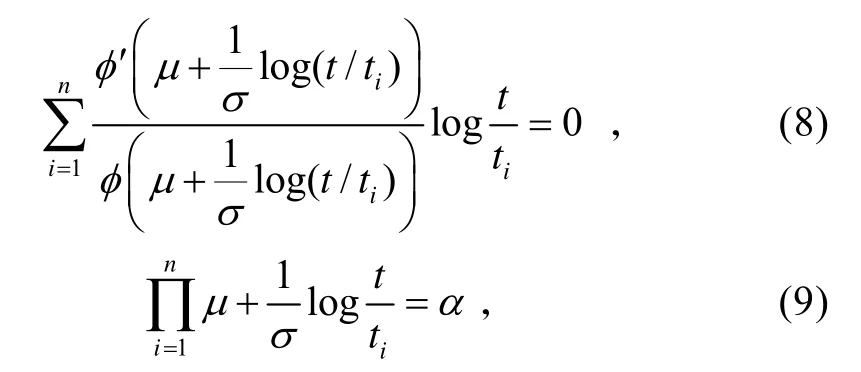
μ (σ)由式(8)求得，设σ=σ1时，得μ=μ (σ1)，设σ=σ2时，得μ=μ (σ2)。

工程上，疲劳寿命试验的对数标准差的范围较大，从0.01到0.2 不等。不妨取 σ1=0.01，σ2=0.1，则，在95%的置信度下，根据表1计算得到的飞行小时数据，如果将首翻期延长为1 200 h飞行，则其可靠度的单侧置信下限为96.1%。

3 结论

1）上述寿命计算的方法是在无原始设计资料的条件下进行的，计算的是相对损伤和相对寿命，该方法为飞机寿命的领先使用（或CBM）奠定了理论基础，也为合理地安排大修梯次创造了条件。

2）寿命管理是个动态的过程。假设供方给定的首翻期寿命为1 000 h飞行，通过对机群1 000 h飞行的飞参数据分析，如果将其首翻期从1 000 h飞行延长至1 200 h飞行，计算结果表明直升机机体结构仍然具有较高的可靠度，再如对1 200 h飞行的飞参数据进行分析……，直至机体结构出现必须进厂修复的缺陷为止。上述思想同样也可以应用于机体结构的全寿命控制。

3）通过对飞参数据重心过载谱的分析，利用飞参数据实现从定时维修到状态维修的转变完全是可行的。

[1]陶梅贞.现代飞机结构设计[M].西安∶西北工业大学出版社,1997∶110-164.

[2]薛军,王智,陈志伟.飞机结构疲劳损伤的工程类比法[J].机械强度,2004,26(11)∶138-141.

[3]王智,刘文挺,王磊.单机结构疲劳分散系数研究[J].机械强度,2009,31(1)∶150-154.

[4]张蕾,王智,陈志伟.单机寿命监控系统设计研究[J].陆航学院学报,2003,2(3)∶70-74.

[5]蒋荟,杨晓华.实时雨流计数法的“三变程”计数原则[J].航空计算技术,2008,10(5)∶5-7.

[6]姚卫星.结构疲劳寿命分析[M].北京∶国防工业出版社,2003∶88-91.

[7]穆志韬,曾本根.直升机结构疲劳 [M].北京∶国防工业出版社,2009∶258-264.

[6]贺国芳.可靠性数据的收集与分析[M].北京∶国防工业出版社,1995∶184-188