VIE-ODDM在电磁散射特性分析中的应用

李尚生，宋亚平，殷 勇，丛 军，陈如山

（1.海军航空工程学院电子信息工程系，山东 烟台 264001；2.91436部队，广西 柳州 545613；3.南京理工大学电光学院，南京 210094）

0 引言

矩量法（MOM）[1]求解体积分方程（VIE）在解决非均匀介质的电磁散射问题中应用非常广泛，它是一种严格的数值方法，其计算结果精度高，但同时具有未知量大的缺点。假设它离散所得的SWG基函数[2]个数为N，那么它需要占用O (N2)的内存，并且通过迭代解法需要执行 O (N2)次矩阵矢量乘的操作。因此，用传统的矩量法很难求解电大尺寸目标的电磁散射问题。

本文将体积分方程方法与重叠型区域分解法（ODDM）[3]结合，得到改进的体积分方程方法（VIE-ODDM），这种分区域求解的方法能够减少每次求解时的未知量，从而可以减少计算机占用内存。另外，由于每个子域边界的电流奇异性得到有效地抑制，因而外迭代过程能够很快地收敛，大大减少了计算时间，特别是在解决电大尺寸的问题上这些优点更加突出。

1 VIE-ODDM 基本原理

用体极化电流J表示体积分方程如下：

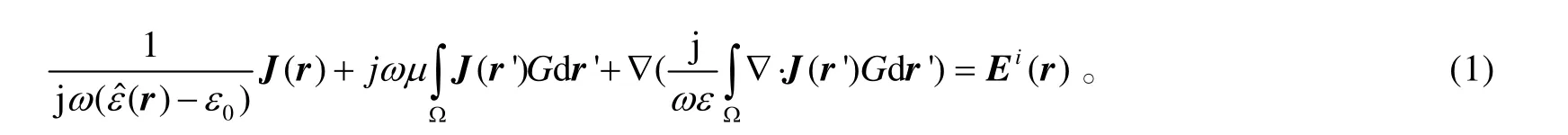
用矩量法求解上式都将转化为求解一个矩阵方程：ZD=V。对于电大结构，阻抗矩阵Z的逆矩阵的计算几乎不可能实现，取而代之用迭代法求解，本文所采用的迭代算法是最小余量法（GMRES）[4]。

区域分解法（DDM）把整个计算区域Ωi分解成若干个子区域 Ωi,i=1,…,M，相应的Z 则被分裂为若干小块矩阵，然后分别求解各个子对角块矩阵方程，再通过迭代方法得到整个矩阵方程的解。由于每次只需对其中的一个块矩阵进行处理，所以降低了内存的消耗，当然因为要通过迭代法得到整个矩阵方程的解，计算时间往往会变长。如果在并行机上进行并行计算，计算效率将会得到提高，也可以通过预条件技术来减少迭代次数和计算时间[5]。

在积分方法中运用DDM时，为抑制子区边界处电流的奇异性，保证收敛性并提高迭代算法收敛速度，在求解某一子域Ωi时，在该子区的所有相邻子区内增加缓冲区Ωb(i)[6]，然后将扩展子区Ω ′i=Ωi+Ωb(i)作为整个求解区域来计算电流，而后遗弃缓冲区的电流并保留子区的电流，该方法即为重叠型区域分解法。

根据上述原理，可建立子区之间积分迭代公式，定义两个关于体极化电流J的线性算子，对于体积分方程(1)

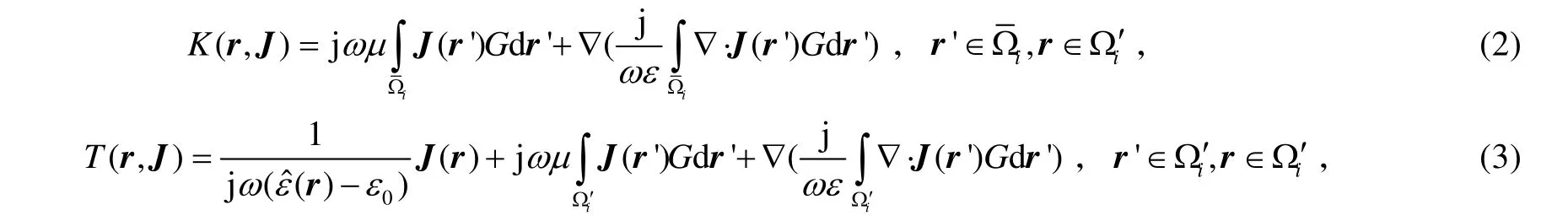
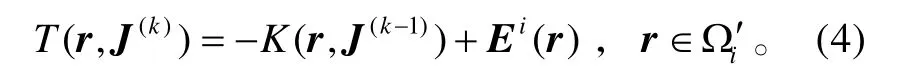
从矩阵角度看，式(4)可表示为矩阵迭代公式：

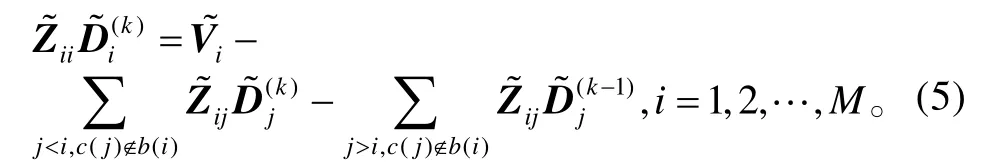
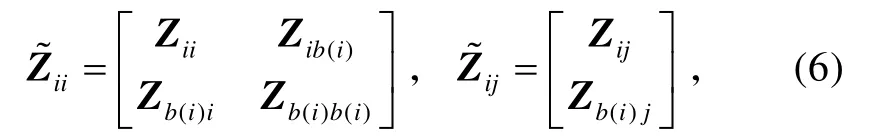
式中：Zii、Zij、Zb(i)i、Zb(i)b(i)分别表示 Ωi内基函数的自作用，Ωj内基函数对 iΩ 内基函数的作用，iΩ 内基函数对Ωb(i)内基函数的作用，Ωb(i)内基函数的自作用；另外的意义见文献[7]。

由于对应相邻子区域的矩阵子块和向量可能重叠，迭代式(5)实际上是变形的Gauss-Seidal 迭代公式。在整个求解过程中涉及到两重迭代：内迭代和外迭代。求解子域的迭代称为内迭代，每求解完一次所有子区域称为一次外迭代。一次外迭代中的内迭代把所有区域的电流依次更新一次。

2 VIE-ODDM计算复杂度分析

设总未知量为N，为方便起见，设每个子区域的未知数个数均为其中Nb为缓冲区电流系数的平均数目。由于总的系数矩阵Z和子矩阵均为满矩阵，迭代求解这两种矩阵方程所需内存分别是ηN2和ξNi2，设VIE-ODDM法的外迭代总共需要ς步。则VIE-ODDM的内迭代所需内存为：

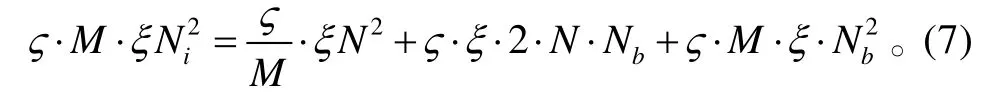
式(5) 右端的矩阵向量积所需内存为Ni⋅(N−Ni)，故VIE-ODDM 外迭代所需内存为：

当总的系数矩阵规模一定时，VIE-ODDM 迭代方式的计算量主要由来决定。

依算例来看，ς 一般取3就可得到足够精度的雷达散射截面。因此，当M 大于3和ξ 小于η，VIE-ODDM 迭代算法的计算量就可减少，计算效率就能得到提高。

3 数值算例

所有算例均设定为：入射波为频率为300 MHz的平面波，极化方向与X轴平行，入射方向为-Z方向。

算例1：计算一个半径为0.20λ的介质球的RCS，相对介电常数为3，整个介质球的SWG 单元个数为1 884。将其分为4个子区，见图1。

图1 半径为0.2λ0的介质球

将VIE-ODDM 求解的结果与MIE级数[8]进行比较，图2中显示数据吻合较好，从而验证了VIEODDM的正确性。

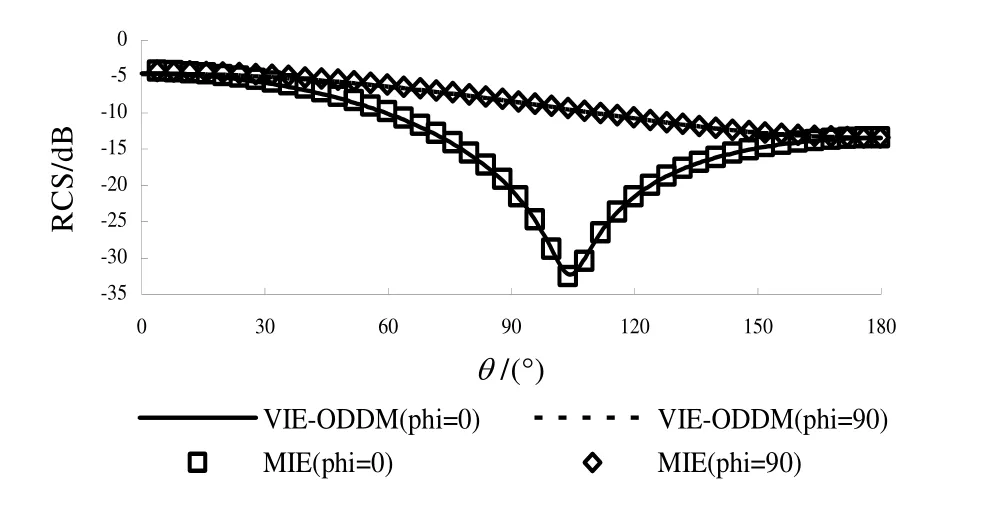
图2 介质球的RCS

算例2：计算一个由3种介质材料构成的长方体的RCS，采用VIE和VIE-ODDM算法，长方体的SWG个数都为3 684。目标结构和材料参数分别见图3。

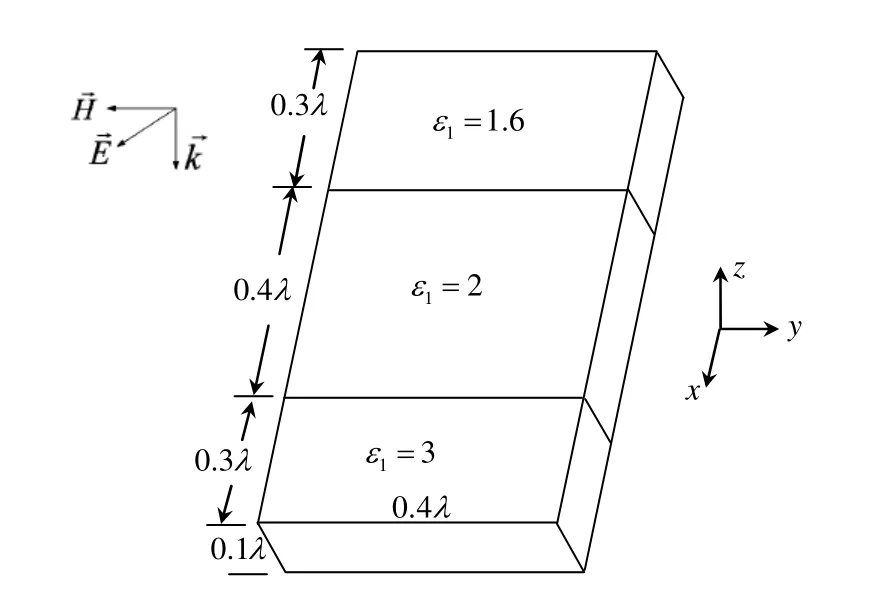
图33 种介质材料的长方体

分别利用VIE和VIE-ODDM 程序计算该目标的双站RCS，结果见图4。

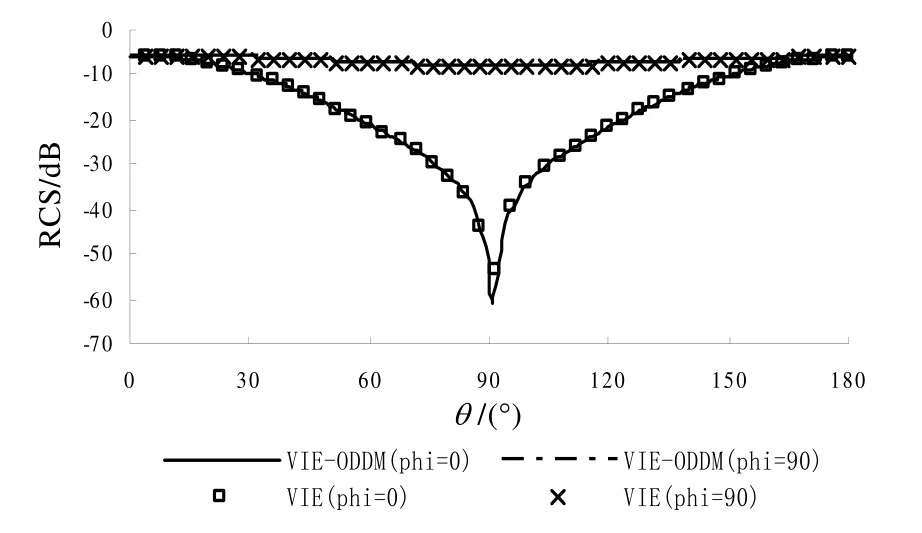
图4 介质长方体的RCS

由图4可见，VIE 程序和VIE-ODDM 程序计算出来的结果相当吻合，见表1。

表1 相对余量误差与迭代次数的函数关系

VIE 经过25次迭代过程，精度达到9.088×10-4，迭代时间为6.9 s，而VIE-ODDM 只经过4次外迭代过程，就达到收敛精度，迭代时间为5.5 s。采用VIE时，所需内存为103 M，而在VIE-ODDM中，求解第2个子区时所需的内存最大，为44 M，只相当于采用VIE 所需内存的42.718%。

4 结论

算例1显示VIE-ODDM的计算结果与解析解吻合较好，从而保证了VIE-ODDM在解决电磁散射问题中的有效性。算例2证明，VIE-ODDM相比于VIE在计算中占用更少的内存，并且通过对两者在迭代次数和迭代时间上的比较，进一步证明VIE-ODDM外迭代过程具有更快的收敛速度。

[1]HARRINGTON R F.Field Computation by Moment Methods[M].NewYork:IEEE Press,1993.

[2]SCHAUBERT D H,WILTON D R,GLISSON A W.A tetrahedral modeling method for electromagnetic scattering by arbitrarily shaped inhomogeneous dielectric bodies[J].IEEE Trans.Antennas and Propagation,1984,AP-32(1):77-85.

[3]LI W D,HONG W,ZHOU H X.Integral equation-based overlapped domain decomposition method for the analysis of electromagnetic scattering of 3D conducting objects[J].Microw.Opt.Tech.Lett.,2007,49(2):265-274.

[4]YOUCEF SAAD,MARTIN H SCHULTZ.GMRES:a generalized minimal residual algorithm for solving nonsymmetric linear systems[J].SIAM J.1986,7(3):856-869.

[5]李卫东.复杂电大电磁散射问题快速算法的研究[D].南京:东南大学,2006.

[6]BRENNAN C,CULLEN P’CONDON M.A novel iterative solution of three dimensional electric field integral equation[J].IEEE Trans.on Antennas Propagat.,2004,52(10):2781-2784.

[7]W D LI,W HONG,H X ZHOU.An IE-ODDM-MLFMA scheme with DILU preconditioner for analysis of electromagnetic scattering from large complex objects[J].IEEE Trans.On Antennas Propag.,2008,56(5):1368-1380.

[8]BOWMAN J J,SENIOR T B A,USLENGHI P L E.Electromagnetic Scattering by Simple Shapes[M].Revised.New York:Hemisphere,1987.