大气湍流对APD直接检测接收机抗噪声性能影响
2011-03-24张铁英王庆官史建国
张铁英,王庆官,史建国
(海军航空工程学院七系,山东 烟台 264001)
无线光通信(Optical Wireless Communications,OWC)可同时满足用户对数据业务的宽带和可移动性需求,而且具有建设实现快捷、保密性强、无须频率申请等特点,近年来受到了各国及军方的广泛关注[1-2]。由于很难保持惟一的电磁波模式以及频率调制和相位调制的复杂性,无线光通信通常采用强度调制/直接检测(IM/DD)系统[3]。
室外无线光通信系统中激光在大气中传输,受天气因素的影响很大。由于大气温度和压力的不均匀性导致激光在传输路径上折射率发生变化,这使得接收信号强度起伏和相位抖动,导致通信质量的下降,特别是湍流影响尤甚。因此,在分析无线光通信链路的性能时,应考虑湍流信道对接收机的影响。湍流根据强弱可分为强湍流和弱湍流两种,其中弱湍流区光强服从对数正态分布,强湍流区用大孔径天线接收时,大气闪烁满足对数正态分布的实验结果[4]。因此,若接收孔径在几十厘米左右,对于距离在几千米以内的光强闪烁可以近似为弱湍流。在处理湍流对系统差错性能的影响时,一般采用求均值的方法,即首先求得高斯噪声信道下的差错概率解析式,然后针对功率(或是光强、信号光场计数等)在区间上求均值,从而得到湍流信道下系统的差错性能[5-7]。这种方法的前提是确知湍流信道的概率密度分布函数,但不同的均值及方差的对数正态分布概率密度形状相差很大,在仿真时要得到理想的结果就必须合理选择积分区间,这便给参数选择带来了一定困难,参数选择不当甚至会出现湍流信道下系统的差错性能好于高斯信道的情况,而且这种方法不能处理点孔接收的情况。
针对于此,本文的处理方法是将光强闪烁作为加性噪声处理(也有部分文献将光强闪烁作为噪声处理,但不是基于雪崩光电二极管(avalanche photodiode,APD)直接检测接收机的[8-9],针对性不强)。先给出APD直接检测接收机的模型,在此基础上推导了基于对数正态分布的直接检测接收机的信噪比以及光脉冲系统的差错性能,分析了湍流对APD直接检测接收机性能的影响,并给出了对抗湍流的措施,讨论了孔径接收尺寸对不同闪烁强度平滑效果以及天线尺寸选择应注意的问题。
1 APD直接检测接收机模型及信噪比
直接检测接收机的模型如图1所示。在这里,我们考虑的噪声有信号光场和背景光辐射光场引入的散弹噪声,APD探测器暗电流噪声以及本地阻抗引起的热噪声。图中:Ps为信号光功率;Pb为背景光功率;m(t)为调制信号;β为调制系数;α=η/hf;η为探测器量子效率;h为普朗克常数;f为光载波频率;g为APD的增益;Noc=2κT/RL;κ为波尔兹曼常数;T为负载温度;e为电子电量;RL为本地负载。
探测器电流、暗电流和热噪声电流之和为总输出电流y(t)。y(t)的功率谱密度为[10]
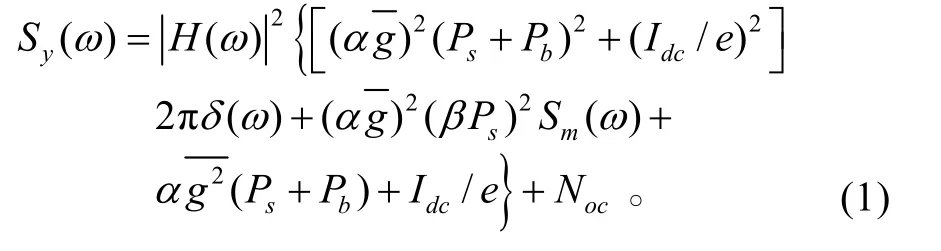
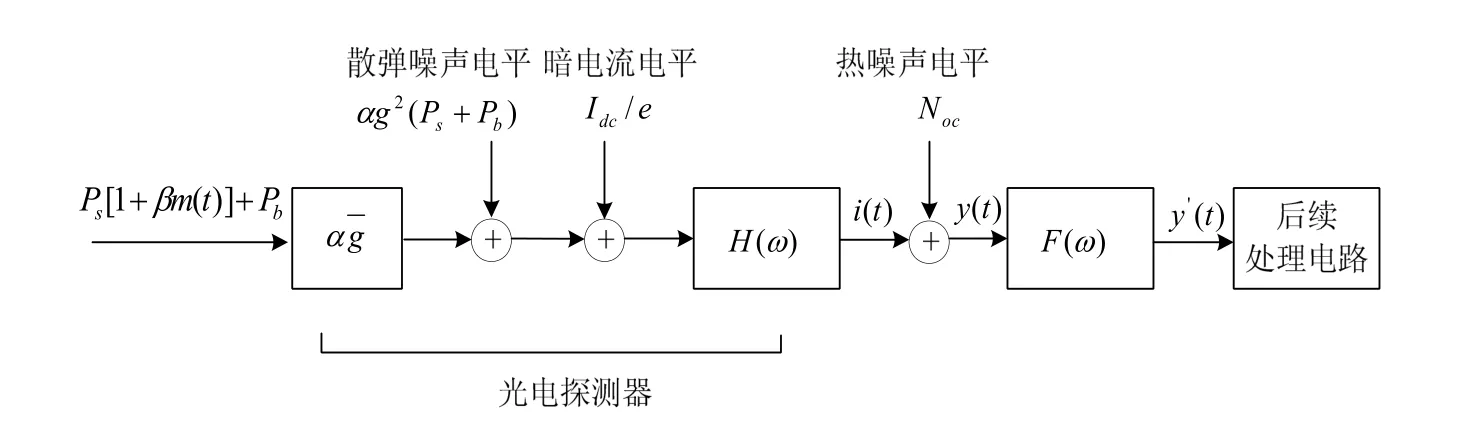
图1 直接检测接收机模型
式(1)将探测器每一种功率谱合并在一起,其中Sm(ω)为调制信号功率谱密度。如输出电流要经过理想增益放大器,则上式的每一项都要乘以放大器增益的平方。由式(1)可知,功率谱中既直流分量,又有交流分量。因为直流分量可以通过滤波器滤除掉,因此直接检测接收机的信噪比只考虑交流分量部分。我们利用一个理想滤波器(如图1中F(ω))将所需的调制信号m(t)滤除出来。
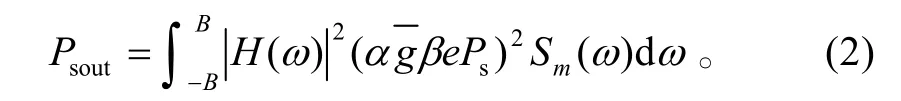
滤波器输出噪声总功率为
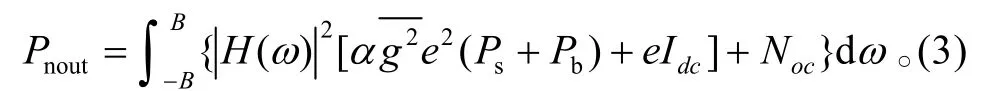
因此,APD直接检测接收机的输出信噪比为
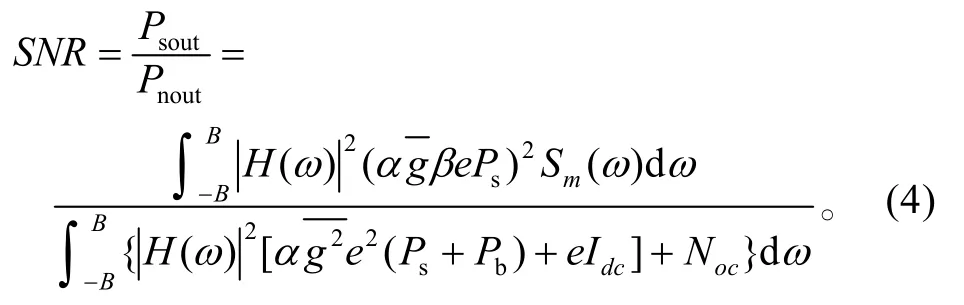
若假定探测器的传递函数H(ω)为理想的,即在[−B,B]上是具有单位电平的传递函数,则式(4)为
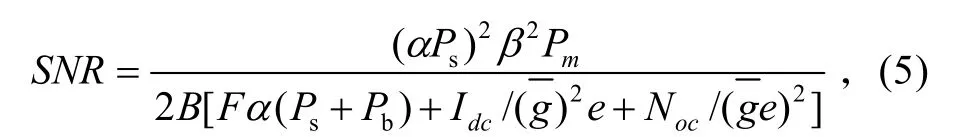
式中:Pm(ω)为调制信号m(t)在[−B,B]内的功率。
2 湍流信道的影响
2.1 湍流信道模型
根据湍流运动状态的不同,光的大气传播信道可分为弱湍流信道和强湍流信道。激光束通过弱湍流大气后闪烁概率分布为对数正态分布,在饱和闪烁区域则可为负指数分布[7]。对于距离在几千米以内的无线光通信系统中的光强闪烁效应,若接收天线孔径在几十厘米左右,考虑孔径平滑效应,此时光强闪烁一般可看作弱闪烁,服从对数正态分布,其概率密度函数为:
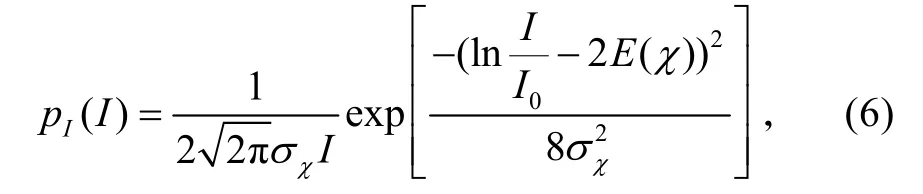
式中:I为接收光强;E(χ)和χσ分别为对数振幅χ的均值和标准差,χσ 也称为闪烁指数。
式(6)的确定需3个参数E(χ)、σχ和I0。但若固定对数正态分布的均值E (I)=I0,则式(6)为[11]
(1)查阅文献不足。很多大学有开设文献检索课,但是课程结束之后,能主动再查阅文献的学生比较少。针对某一个研究方向进行相关的检索总结就更少了。
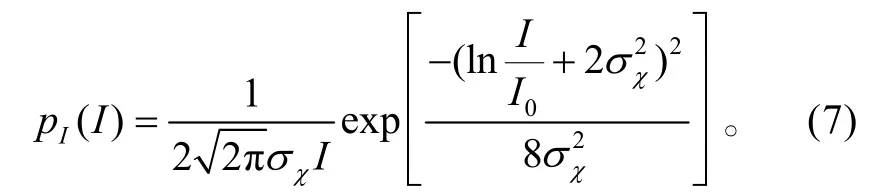
图2给出了闪烁指数χσ为不同值时的概率密度函数的图形。
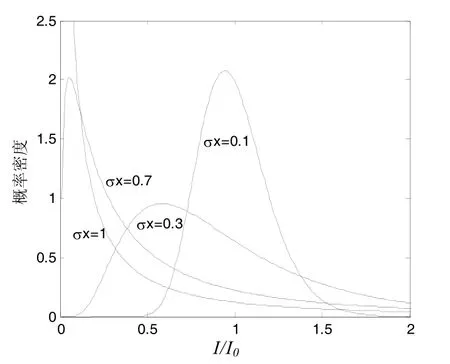
图2 对数正态分布的概率密度
由图2可知,即使均值相同,不同闪烁指数的波形也是不同的。随着闪烁指数的增大,光强的分布越来越散。对正态分布一般认为适用于 σχ≤0.3弱湍流的情况。
2.2 湍流信道下的APD直接检测接收机性能
当直接检测接收机在湍流信道下工作时,由于接收到的光场因湍流的影响是随机的,在天线上收集的信号功率也将随机变化,这相当于引入了功率起伏噪声,并由功率方差给出。功率与光强的关系由下式给出:
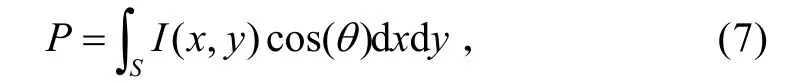
式中,θ是(x,y)点处接收天线平面S的法线与光场传输方向单位矢量之间的夹角。为了便于推导,我们假定光强在天线平面上是均匀的,以及根据I=I0exp(2χ),则功率方差为
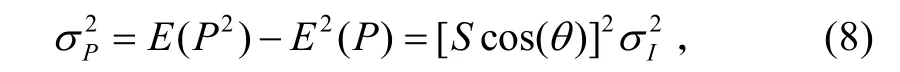
根据文献[11]可知
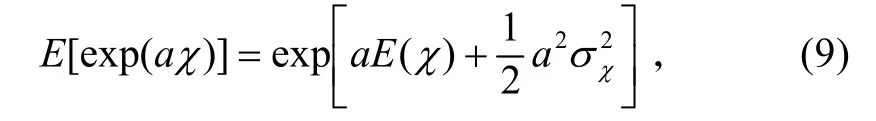
a为任意复数,可得
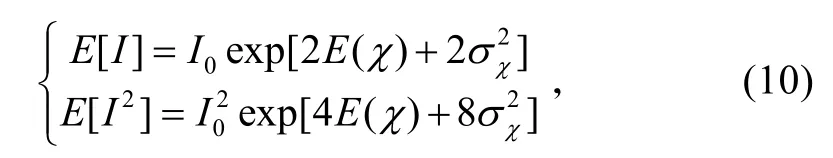
所以光强的方差为
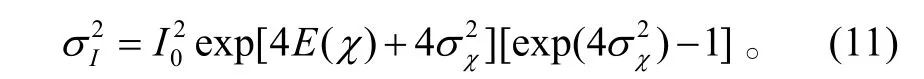
将式(11)代入式(8)有
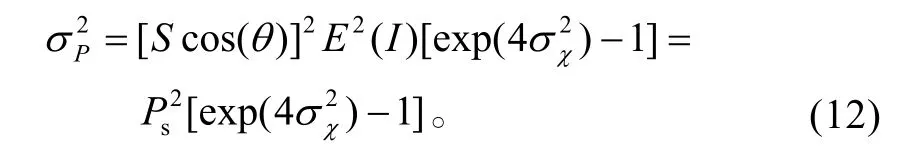
这里 Ps=I0S cos(θ)。因此,考虑湍流影响下的APD直接检测接收机的信噪比为
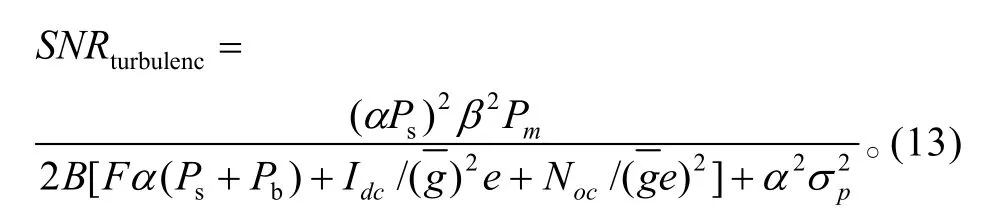
若通信链路是基于APD直接检测接收机的数字光脉冲系统并采用曼彻斯特编码,则图1中的模型需要增加比特积分器和比较器等部分。经推导其误比特率为
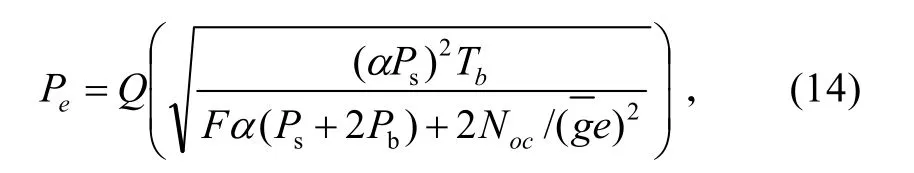
式中:Tb为曼彻斯特编码的时隙宽度。
考虑湍流的影响,则上式修正为
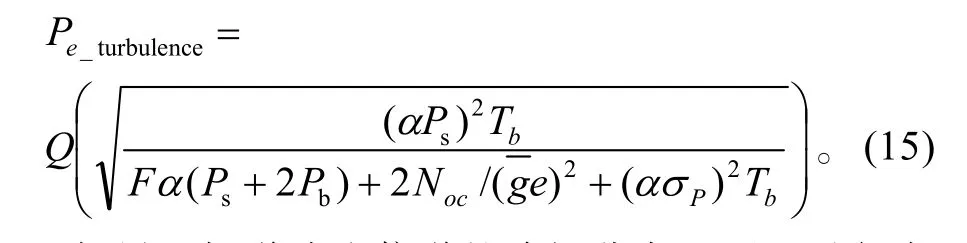
如果不知道湍流信道的确切分布,可以进行实地观测,从而得到功率起伏的方差,然后将其代入式(13)、(15)即可。
3 数值结果
本文主要基于推导所得的式(12)、(13)及(15),具体分析湍流对APD直接检测接收机可靠性的影响,并与非湍流状态比较。由于大气对光的吸收会随光频率的不同而变化,且光电探测器的材料决定其响应波长。因此,选取较高大气透射率的1.55 μm激光作为调制光源,同时忽略暗电流的影响,并令β2Pm=1。主要参数选择见表1。

表1 数值仿真参量
首先,在大气闪烁指数分别为0.1、0.2、0.3条件下,分别对APD直接检测接收机的信噪比和曼彻斯特编码系统的误码率进行分析,数值结果如图3、图4所示。从图中可以看出,大气湍流严重地削弱了APD直接检测接收机的差错性能。当接收功率为−46.5 dBmW时,若无湍流影响,APD直接检测接收机的信噪比约为5 dB,曼彻斯特编码系统的误码率数量级接近10-7,而存在湍流扰动且闪烁指数分别为0.2、0.3时,对应的信噪比下降至约2.6 dB和1.5 dB,对应的误码率数量级下降至10-2和10-1。
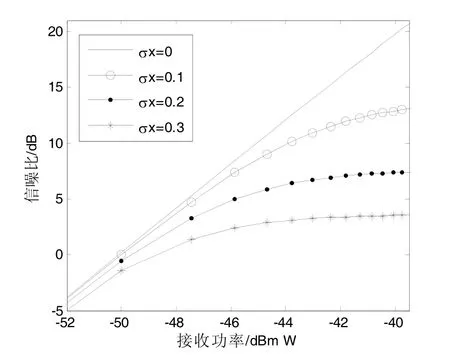
图3 不同闪烁指数下APD接收机信噪比
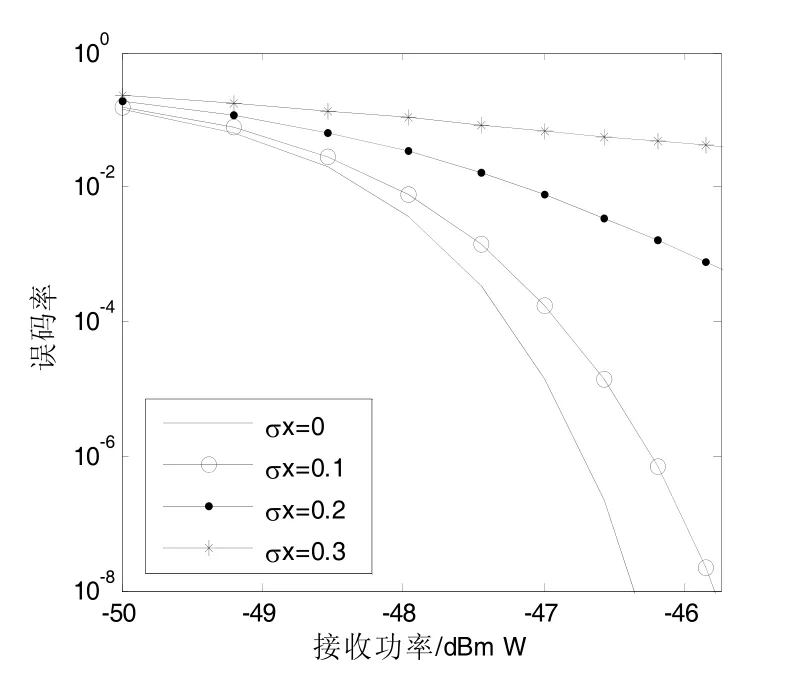
图4 不同湍流指数下曼彻斯特编码系统误码率
需要注意的是当闪烁指数较大时,如 σχ=0.3,随着发射功率的增大,接收机的信噪比和差错性能并无显著增加,即增大发射功率并不能有效提高接收机的抗干扰性能。
我们在推导APD直接检测接收机的信噪比和曼彻斯特编码系统的差错性能时,考虑的是点孔接收。当用检测孔径 2r>>r0的天线接收光场时,考虑到孔径平滑效应,闪烁指数可改写为[12]
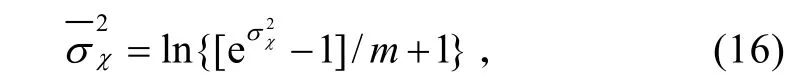
式中:r0为相干长度,即激光穿过大气时,在其横截面上两点间相位保持相干的最长距离;m为接收孔径内互不相干散斑元的个数,接收孔径越大,散斑元的个数越多。
为了更好地分析孔径平滑效应对APD接收机的影响,图5和图6给出了考虑孔径平滑效应的APD接收机信噪比及曼彻斯特编码系统误码率的数值结果,这里m的值分别取3和4。由图可知,孔径平滑效应能够有效地改善APD接收机的抗噪声性能。当接收功率为−46.5 dBmW,σχ=0.2和σχ=0.3时,在m=4的情况下,APD接收机的信噪比同比分别增加了约1.5 dB和1.8 dB,曼彻斯特编码系统的误码率同比分别降低了近两个数量级。虽然孔径平滑能够有效地改善APD直接检测接收机的抗噪声性能,但对不同的闪烁指数下的影响却是不同的。当闪烁指数σχ=0.3,m=3和m=4时,要达到误码率为10-4,对应的平均接收功率分别为−45.7 dBmW和−46.2 dBmW,即当m 从3 增加到4(相当于增大接收孔径),可以节省0.5 dBmW的接收功率,而闪烁指数σχ=0.1时,节省接收功率仅为0.05 dBmW。也就是说湍流强度较强时,孔径平滑效应比湍流强度较弱较时要明显。
需要指出的是,增大接收孔径可以减小湍流的影响,但同样会引起背景噪声的增加,这将会减弱APD直接检测接收机的抗噪声性能。除此之外,天线孔径过大,其成本也会急剧上升。
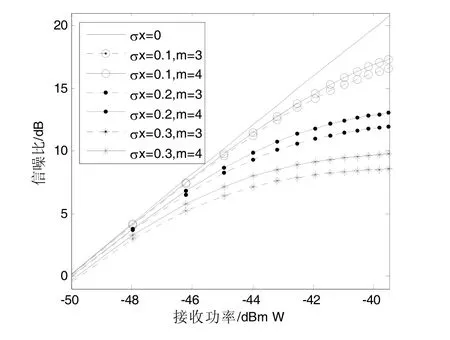
图5 考虑孔径平滑效应的APD接收机信噪比
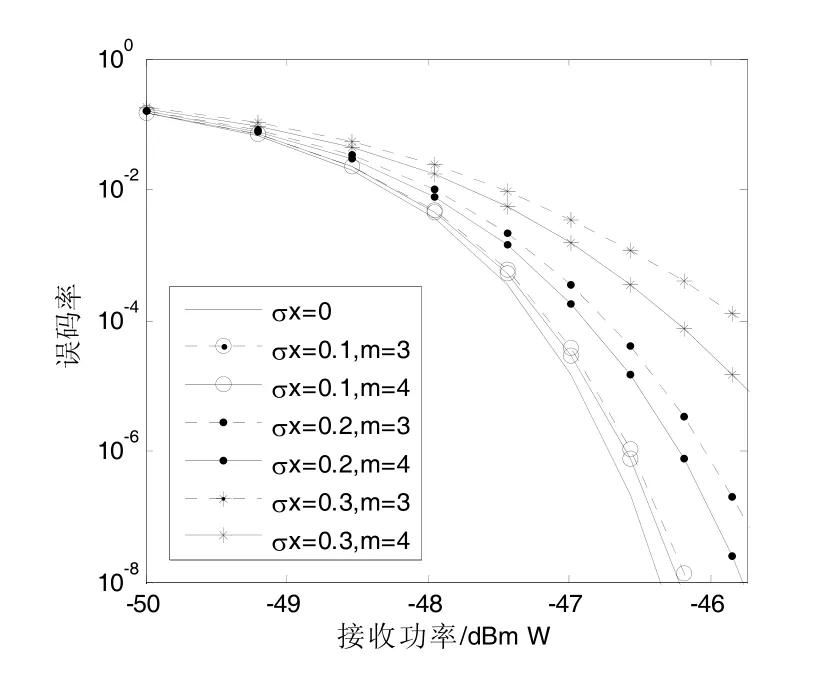
图6 考虑孔径平滑效应的曼彻斯特编码系统误码率
4 结束语
本文在大气湍流下,推导了APD直接检测接收机的信噪比和曼彻斯特编码系统的差错概率,详细分析了湍流对APD直接检测接收机的抗噪声性能,并且给出了对抗湍流的措施。湍流引起的功率起伏严重地削弱了APD直接检测接收机的抗噪声性能,在天线尺寸较小的情况下(天线直径小于相干长度),增加发射功率并不能有效地提高系统的可靠性;增大接收天线孔径可以显著减弱湍流的影响;湍流强度较强时,天线孔径平滑效应比湍流强度较弱较时要明显。但当接收孔径增加到一定尺寸时,发射的信号大部分被接收,此时接收功率均值不会再增加,而背景光噪声功率则持续显著增大,将会有效减弱APD直接检测接收机的信噪比。此外,本文推导的结果稍加修改即可用于PPM、DPIM 等其它调制方式,为大气无线光通信系统设计提供参考。
[1]ZHU XIAOMING,JOSEPH M KAHN.Free-space optical communication through atmospheric turbulence channels[J].IEEE Transactions On Communications,2002,50(8)∶1293-1300.
[2]张铁英,王红星,程刚,等.无线光通信中的定长数字脉冲间隔调制[J].中国激光,2007,34(12)∶1655-1659.
[3]MARVIN K SIMON,VICTOR A VILNROTTER.Alamouti-type space-time coding for free-space optical communication with direct detection[J].IEEE Transactions on Wireless Communications,2005,4(1)∶35-39.
[4]谢良伟,汤俊雄.基于Turbo 码的大气无线光通信系统特性分析[J].中国激光,2003,30(9)∶835-838.
[5]谢良伟,刘璐,汤俊雄.无线光通信差错控制系统的时间参数特性[J].中国激光,2004,31(5)∶575-578.
[6]胡宗敏,汤俊雄.大气无线光通信系统中数字脉冲间隔调制研究[J].通信学报,2005,26(3)∶75-79.
[7]KAMRAN KIASALEH.Performance of APD-based,PPM free-space optical communication systems in atmospheric turbulence[J].IEEE Transactions on Communications,2005,53(9)∶1445-1461.
[8]邓代竹.大气随机信道对无线光通信的影响[D].成都∶西南交通大学,2004∶26-28.
[9]王丽黎,柯熙政.湍流效应对光通信链路的影响研究与仿真[J].光散射学报,2004,16(3)∶250-255.
[10]ROBERT M GAGLIARDI,SHERMAN KARP.光通信技术与应用[M].陈根祥,秦玉文,赵玉成,等译.北京∶电子工业出版社,1998∶50-95.
[11]张逸新,迟泽英.光波在大气中的传输与成像[M].北京∶国防工业出版社,1997∶110-166.
[12]YURA H T,MCKINLY W G.Optical scintillation statistics for IR ground-to-space laser communication system[J].Appl.Opt.,1983,22(4)∶3353-3358.
