基于遗传算法的排课编码设计

李梅云



基于遗传算法的排课编码设计

李梅云

（漳州职业技术学院 计算机工程系，福建 漳州 363000）

采用遗传算法的基本理论，研究如何利用遗传算法解决高校排课中的教室冲突、时间冲突、教师冲突和课表优化等问题，根据人们的期望值设定遗传算法染色体的优先级。

教学管理；排课系统；遗传算法；数据库；时间片

随着职业教育的发展，学院规模的扩大，面对越来越多的学生和有限的教学资源，单纯的以手工来完成学院的教学管理工作效率跟不上需要，须采用一种更快捷的处理方式。作为教学管理工作重要项目的排课，利用计算机进行排课能够快速地得到满足约束条件的可行结果，具有时间短、人力省和质量高的优点。目前排课算法有“反复比较法、优先级法、整体规划法、蚁群法、遗传算法等等。

1 排课约束条件分析

排课问题是一个NP完全类【1】，主要要考虑排课的硬性约束条件和软性约束条件。协调好排课五种要素：班级、教室、教师、课程、时间。排出的课表尽可能实现三赢，即满足学校、班级和教师三方的需求。

1.1 排课问题的要素

要排一张好的课表，首先就要对教学资源进行调查和统计，清楚所有教学资源，这样才能做出一张尽量不出现冲突，也能最大发挥教学资源利用率的完美课表，下面就排课所涉及到的因素进行分析。

课程是排课因素里一个很重要的要素，每一门课程都有其课程的编号、名称、是理论型课还是实训课、学时、学分、该课程的教师资源情况、授课对象情况、开设的院系、所需要的教学设备，每一门课程都有对应的授课计划，是否一个学期上完。每门课程既可以指定教师，又可以不指定教师。有些课程可以有多个班级合并上课，有时候是跨院系的。每门课程都有对教室类型的相关要求。如多媒体教室、一体化教室、语音室、实验室等等。某些课程由于上课班级较多难以协调或照顾教师要求等诸如此类原因，应该预先给定时间或教室。

班级是教学的基本单位，应有编号、专业名称、学制、所在院系、辅导员等信息。在排课时要可虑到班级学生人数的多少、层次，便于在排课时发现班级人数少的班级在上公共课时可虑合班上课，节省教学资源。我们学校把全校的教室按系进行分配如我们学校有成业楼、兴业楼、敬业楼等教学楼，把这些教学楼分配给各系，让各系自行支配所分得的教学楼。在此种情况下，在排课时会减低教室使用的冲突。

时间是排课中无形的但又左右排课的一个要素。学校时间一般为学年、学期、周、星期几、时段、节。每天分三个时间段（上午、下午和晚上）。每个时间段又进行分节，如上午为1、2、3、4，下午为5、6、7、8，晚上为9、10。一节就是一个课时，是上课的最小单元，一般一门课程的上课是按两节课来进行，所以可以把时间划分为5个时间片，如表1所示用T1,T2,T3…T25表示。时间冲突决定了课表的实用性，因此要把时间进行科学的合理的组织和分配。

表1 周时间片

教师是教学活动的一个主体，能否合理、有效、充分利用教师资源，决定学校的办学质量和水平。学校教师可分为教学型、研究型和教学研究型三种。在录入教师基本情况时，都要对他们进行详细的登记如姓名、编号、学历、职称、研究方向、所能胜任的课程等。

作为基本教学管理的院系单位，在排课时应该充分考虑各院系的不同，尽量协调，达到和谐，比如不要出现院系办公室没人的情况。包括院系名称、编号、所在校区、办公室人员。

班级做为教学活动的另外一个主体，应考虑学生上课的最佳时段，尽量把课程安排在该时段上课。提高学生的学习兴趣，从而提高教学水平。每个班级都要设置专业、班号、年纪等。

教室是实施教学活动的场所，每一间教室都有其特有信息，比如该教室处于哪个校区，归哪个系所有，这间教室可以容纳的学生数，是什么类型的教室等等。

1.2 排课问题的约束条件

众所周知，排课是一种多组合问题【2】。它不仅要考虑很多的资源如教师、教室、时间、班级等，还要考虑排课问题自身的约束条件。根据现有的文献，可以看到，一般把约束条件分成两种，一种是硬性约束条件，另外一种是软性约束条件。所谓的硬性约束条件就是在排课过程中一定要满足的条件，而软性约束条件就是尽量满足的条件，如果满足了，可以使排课的效果更佳，但如果没有满足，也没关系，不会影响排课。排出来的课表在实际情况中是否可行就得由硬性约束条件来衡量，而课表是否优秀就要采用软性约束条件来评判。下面列出一些硬性约束条件和软性约束条件。

1）硬性约束条件

（1）一个班级不能同时段在两个或两个以上教室上课；（2）一位老师不能同时段在两个或两个以上教室上课；（3）一间教室不能同时段有两门或两门以上的课程同时占用；（4）教室的座位数必须大于等于上课的学生人数。

2）软性约束条件

（1）理论上说上午的时间上课效果优于其它时间，其次是下午、晚上；（2）要尽量为专业课程安排上课效果好的时间段；（3）是连堂类课还是分散类课；（4）中午、周末尽量不要排课；（5）尽量不要在体育课完后排课；（6）一个班级应尽量避免安排在连续的时间段上相同的课程；（7）尽量安排教师在比较集中地时间上同一门课；（8）先排专业课，再排基础课、公共课。

在对教学资源和约束条件都比较清楚情况下，就可以在有限的教学资源下，充分运用约束条件来解决排课问题。先来看一个例子，假设就一个班级，那么学校的所有资源就只有这个班级使用。这种情况下就不用考虑会发生冲突，就表2这样的一个简单的二维表就可解决。但实际情况是学校不可能只有一个班级，随着班级数的增多，冲突也就跟着增多，约束条件也会越来越多。而排课问题又是一个多组合和不确定性的组合规划问题的求解，约束条件越多，求解越困难。

表2 简单课表

但随着班级的增加，开课计划数的增加，其组合方案为（其中n为所有班级要排课的计划数，m为需要排课的班数）将会迅速增加【3,4】。在一个大学里班级数多，且排课的计划数组合方案会随着n和m的增加，呈线性增长。如何控制这种增长，是我们排课的关键。对于排课这种没有确定解的组合问题，在排课时，不可能只有一个解，它可能有多个解，在选择解时，就要选择那种不发生硬性约束条件冲突的，包含所有年级、课程、班级的，可以满足较为多种的软性约束条件的解。尽管一次好的排课，在人们理解是也只是使用如优秀、合理、完美等这些文字来形容，没有一个数量上的概念；但在实施具体排课时，就要把人们的这种模糊的、不确定的因素量化。

2 遗传算法求解排课

用遗传算法求解排课这样一个实际问题时，首要要做的是如何把这个排课问题表示成染色体，使之便于实施遗传算法。在本文中每一条染色体代表着一个班级的课表，可采用十进制进行编码，染色体的结构可用下面的结构表示出来：

染色体以十进制数编码为例，例如09嵌入式2的班级编号是21100902，有一门课为计算机导论，该课程的课程编号是0103010，上这门课的教师编号为33，学时为4，随机选择大于班级总人数的教室，则可生成染色体如：“21100902010301033B5020211”，其中B502代表教室，02、11分别代表上课时间是星期一上午的3、4节和星期三上午的1、2节。每一条染色体表示一种可能的排课结果。这样就可排出所有班级所有课程，但在实际的排课中还涉及到资源冲突问题。如所排的课表是否有时间、教室、教师等方面冲突，所以还需要适应度函数来评判排课结果的优劣。

由于适应值是遗传算法中个体生存机会选择的唯一确定标准指标，所以适应值函数的形式直接决定着群体的进化行为。在本文中，适应度函数的设计是先设定各种硬性和软性约束条件的期望值，再对每条染色体中存在的硬性和软性约束条件的期望值进行求和。表3、4、5、6列出一些排课相关因素的期望值。则适应值就可设置为f=∑si（i =1…k）。其中si表示某条约束条件的期望值染色体适应度函数值越大，则表示适应性越好，其在下一代的演化中的生存概率就较大。

表3 同一班级上课时间间隔的期望值

表4 同一教师上不同班级的同一门课时间间隔的期望值

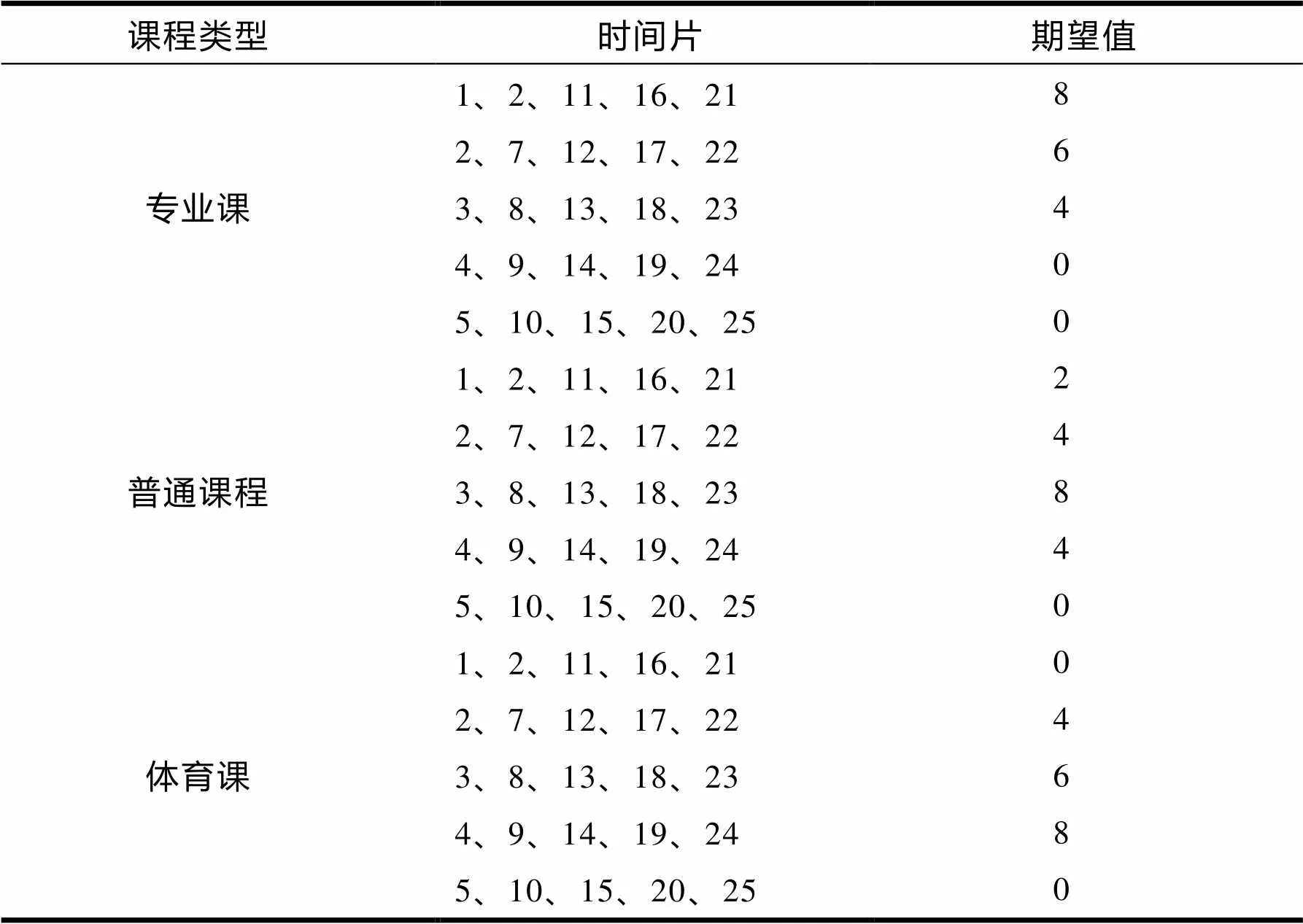
表5 不同课程上课时间的期望值

表6 同一教师上不同课时间间隔的期望值

2.1 初始化

初始化的作用主要为后面的遗传操作提供初始种群。而在不具有问题解空间先验知识的情况下，很难判定最优解的数量和其在可行解空间中的分布情况。因此初始群体的个体一般多是随机产生的。在算法中，是以班级作为染色体的，所以在初始化时就需要考虑跟班级相关的因素。对于一个班级来说班级上课不外乎涉及到上课的教室，上课时间，上课科目，上课教师这几个因素。

在此算法中采用先对教室的容量与该班级的人数做比较，把大于班级人数而且教室多出的座位不超过10各座位的教室设置为一个教室空闲集room(),再对每一个班保留一个空闲时间集hour(c)。先把教师和课程安排进去再搜索时间空闲集hour(c)，把时间分配给该课程；搜索教室空闲集room()，把教室分配给该课程。重复上述过程，直到生成初始的一个班级的课表。以此得到个个班级的初始课表。

2.2 选择算子

选择运算又称复制操作，它是模拟自然界适者生存、优胜劣汰的自然选择现象。它以一定的概率从种群里选择若干对个体的操作，放入下一代种群中，接下来的交叉操作和变异操作都是以此为依据的。

在系统设计时采用了轮盘赌选择法。某染色体被选中的概率可表示为pi=fi/∑fi，式中fi为种群中第i个染色体对应的适应值，∑fi是种群中所有染色体的适应度值之和。

2.3 交叉算子

选择操作可以使种群里比较好的染色体，遗传到下一代；但选择操作只是做选择，不能创造出新的染色体，因此，还需要交换操作，交叉也称杂交、交换。

在排课系统中，因为编码是以数据库记录字段为单位进行的，而且影响排课问题的元素本身相互之间有关联，所以不能利用简单的单点交叉和双点交叉。本文的交叉算子选择多点交叉的方式进行，在编码时，编码的顺序是班级、课程、教师、教室和时间。将这些编码分成三个段：班级、课程与教师一组、教室一组和时间一组，在交叉时随机选择两条染色体，然后再随机的在对应的某两段之间进行交换。

2.4 变异

变异运算用来模拟自然界中生物的基因突变，让遗传因子以一定的概率变化，这种变化的概率通常都比较小。在系统中，利用变异算子的局部的随机搜索可以加速向最优解逼近的能力，当运算接近最优解区域时，先设定变异算子为教室中的任意时间片。

3 结束语

根据漳州职业技术学院实际情况，本文通过对人们的期望值设定遗传算法染色体的优先级，并设定时间空闲集和教室空闲集。基本解决了高校排课中的教室冲突、时间冲突、教师冲突和课表优化等问题。

高校排课系统一直是教务管理中重要、复杂的问题,除了对系统进行精心设计外还要在排课过程中,还要充分发挥个人主观能动性,把学生的利益放在第一位,同时兼顾教师和校方的利益。另外，排课人员需要掌握各种现代化管理技术,不断改进排课的方法,促进教育信息化建设,这也是高等教育改革向纵深发展的必然要求。

[1] 蔡振锋.遗传算法在高校排课中的应用[J].湖北工业大学学报,2006(1):35-38.

[2] 霍然.自然与人工系统的适应性[M].北京:高等教育出版社,2008.

[3] 陈乔礼,吴怀宇.一种新的求解旅行商问题的混合遗传算法[J].武汉科技大学学报：自然科学版,2007(1):19-22.

[4] 王晓倩,陈定观,林礼区.高校实验教学排课系统的设计与开发[J].科技资讯,2009(2):27-31.

The Course code design Based on Genetic Algorithms

LI Mei-yun

(Department of Computer Engineering,Zhangzhou Institute of Technology,Zhangzhou 363000,China)

The author uses the basic theory of the genetic algorithm to study how to solve the problems of resource conflict and curriculum optimization by way of genetic algorithm. The system allows people to set the priority of chromosome genetic algorithm according to people's expectations.

Teaching management；curriculum-arrangement；system；genetic algorithms；time slice

2011－06－25

李梅云（1981－），女，福建莆田人，助教，硕士。

TP311.52

A

1673-1417（2011）03-0022-06

（责任编辑：季平）