基于决策表的模糊粗糙单调依赖算法及其应用*

梁瑾罗飞许玉格

(1.华南理工大学自动化科学与工程学院，广东广州510640;2.华南师范大学教育信息技术学院，广东广州510631)

粗糙集［1］是用来处理不确定和不完整数据信息的数学工具，模糊集［2］也可以描述信息和知识的不确定性，两者具有很强的互补性，因此可以把它们结合起来对信息进行不确定性处理.在决策表中，粗糙集挖掘条件属性和决策属性之间的依赖关系、约简属性，找出哪些条件属性对决策属性比较重要，其理论基础是等价关系.针对等价关系的局限性，人们提出了不同的约简关系，文献［3-4］中提出了领域和相容关系，Greco等［5］提出了优势关系，Dubois等［6］提出了模糊等价关系.事实上条件属性和决策属性之间往往还存在量的单调依赖关系.例如在生化反应中，条件成分和成品之间在一定范围内有单调递增或递减依赖关系，一般情况下越多的成品需要越多的条件成分，但是否凡是包含成品成分的条件成分都与成品之间有这样的单调递增关系呢?显然不是.有些条件成分虽然包含成品中的成分，但它们并不参与生成成品，当然在某些情况下可以通过确定的生化反应方程较精确地计算出来.但大多数情况下，生化反应处于一个复杂的环境中，受到很多物理、化学和生物等不确定因素的影响，因此可以采用模糊粗糙的方法，先计算出条件成分与成品之间的单调递增或递减关系，从而精简掉冗余的条件成分，然后进行相应的分析，即挖掘出哪些条件属性的变化会影响决策属性量的变化，并且挖掘出哪些量影响的程度大，得出主要控制哪些条件属性的量会影响决策属性量的变化，从而达到控制的目的.

Wu［7］和Chou等［8］分别讨论了模糊单调函数及其在逻辑控制中的应用，文献［9-12］中讨论了Mamdani-Assilians模型和T-S推断方法的模糊控制单调问题，文献［13-14］中讨论了决策表属性约简算法.根据模糊粗糙集理论，文中提出了一种基于决策表的模糊粗糙单调依赖算法，首先通过区间映射重新定义了基于决策表的模糊单调依赖概念，用于挖掘条件属性和决策属性之间的单调递增依赖关系，然后证明了相关命题，根据命题得出相应的结论，并将该算法初步应用到污水处理中.

1 模糊粗糙决策表

1.1 决策表

知识表达系统也称为信息系统，可以用四元组S=(U，A，V，Q)来表示.其中:论域U为对象的非空有限集合;A为属性的非空有限集合;为属性a的值域;Q:U×A→V为信息函数，它为每个对象的每个属性赋予一个信息值，即∀a∈A，x∈U，Q(x，a)∈Va.当A=C∪D且C∩D=∅时，C称为条件属性集，D称为决策属性集，称该知识表达系统为决策表［15］.

1.2 模糊隶属函数

设论域U上的一个模糊集合A由U上的一个实值函数来表示，即.对于x∈U，函数值μA(x)称为x对于A的隶属度，而函数μA称为A的隶属函数.模糊集合的运算及性质很多，文中主要使用其交运算，对于y∈U，μA(y)∧μA(x)中的∧表示取下确界［16］.

2 基于决策表的模糊粗糙单调依赖算法

某些知识系统的条件属性和决策属性之间不仅存在离散的、有限集合的简单粗糙决定关系(即仅通过等价关系就可以挖掘出条件属性和决策属性的重要依赖关系，从而得出核条件属性和约简)，还存在量的单调依赖关系，这种依赖程度决定着某些条件属性的变化将对决策属性的变化产生多大影响.某个条件属性的变化对决策属性的变化几乎没有或仅有较小程度的影响，意味着决策属性的变化并不依赖于该条件属性，从而可以挖掘出对决策属性变化产生重要影响的条件属性，并通过控制这些条件属性去影响决策属性.

在决策表中，假设决策属性量的变化依赖于某些条件属性量的变化，因此需要挖掘出对决策属性量的变化产生重要影响的条件属性，称这样的决策属性和条件属性之间有重要的单调依赖关系，但这种依赖关系在决策表中并非一定严格单调.把条件属性值和决策属性值按单调性划分为若干个区间后，如果条件属性值按区间与决策属性值单调映射，那么它们就是依区间单调依赖.为了区别于严格单调依赖，文中称这种依赖关系为模糊单调依赖关系.由于单调递减的依赖关系与单调递增相类似，因此文中只讨论单调递增的情况.

2.1 映射及严格单调依赖

假设对象、决策属性和条件属性之间是一一映射关系，条件属性值集合Ci={xi1，xi2，…，xin}，其中Ci∈C，C={C1，C2，…，Cm}，n和m为待定数，决策属性值集合D={y1，y2，…，yn}，对象值集合U'={e1，e2，…，en}，则对任意对象，有xij∈Ci和yj∈D与它相对应.

命题1如果对任意ek，el∈U'，有yk≥yl⇒xik≥xil，则有xik≥xil⇒yk≥yl.

证明假设xik≥xil⇒yk≥yl不成立，那么同时有xik≥xil和yk≤yl.由yl≥yk⇒xil≥xik，得出xik≤xil，这与xik≥xil相矛盾，因此假设不成立，命题得证.证毕.

根据上面的设定，决策属性和条件属性之间是一一映射的关系，必然存在映射，其中对任意的，也必然存在逆映射同样存在映射xmk}，同理有逆映射对于某个条件属性集，存在映射，使得，同样有逆映射文中仅讨论某个条件属性与某个决策属性模糊单调递增的依赖关系.

2.2 区间划分及模糊单调关系定义

对决策属性集合D中的元素值按递增顺序排列后得到新的集合，通过上面定义的映射，可以得到排列后的条件属性集合因为，所以显然，如果也是按递增顺序排列的集合，那么决策属性D和条件属性C满足定义1，它们是严格单调递增依赖关系.在实际应用中，由于存在各种干扰因素和误差，条件属性和决策属性之间可能是单调递增依赖关系，但并非严格单调递增依赖关系，大部分情况是当决策属性在某个区间的值大于在另一个区间的值时，与决策属性相对应的条件属性在这个区间的值也大多大于在相对应的另一个区间的值.由于是一种模糊的关系，因此，文中称这种情况下的决策属性和条件属性关系为模糊单调递增依赖关系.下面先讨论一种区间划分方法，然后再给出模糊单调递增关系的定义.

假设把决策属性集D'划分为p个区间，考虑到决策属性值分布的不均匀性，文中等距离设定D'的p个区间的中心点，把作为相邻区间中心点的距离，第一个区间的中心点记为，第二个区间的中心点记为ct2(ct2=ct1+dis)，第i个区间的中心点记为cti，那么第i+1区间的中心点cti+1=cti+dis，可得到p个区间中心点的集合{ct1，ct2，…，ctp}.把与中心点集合中某中心点的距离小于等于dis/2的决策属性值归为一个区间:设，且，那么把归为区间Ωi，文中称这种划分方法为Ψ划分.D'经过Ψ划分后，得到Ω1，Ω2，…，Ωp，其中Ω1∪Ω2∪…∪Ωp=D'，Ω1∩Ω2∩…∩Ωp=∅，对任意的1≤r＜h≤p，有sup(Ωr)≤inf(Ωh)，通过映射f，可得到C'i的区间划分为Γ1，Γ2，…，Γp，简称为Z划分，其中对任意Ωk∈{Ω1，Ω2，…，Ωp}，1≤k≤p，有f(Ωk)=Γk∈{Γ1，Γ2，…，Γp}，如果对任意的1≤r＜h≤p，有sup(Γr)≤inf(Γh)，那么决策属性D与条件属性Ci明显满足定义1，是严格单调递增依赖关系.否则，设num(minΓh≥Γr)表示Γr中某些元素的个数，而这些元素的值是小于等于Γh的最小值中元素的个数，可得到定义2.

定义2一个模糊递增依赖隶属函数为

称μ(Γh，Γr)为Γh相对区间Γr的模糊递增依赖程度函数，其中ε为可选参数，0＜ε≤1，可以根据具体情况进行选择，因此μ(Γh，Γr)=0或ε＜μ(Γh，Γr)≤1.当μ(Γh，Γr)=0时，认为区间Γh相对区间Γr没有发生模糊递增的情况，否则称Γh相对区间Γr依程度μ(Γh，Γr)模糊递增，μ(Γh，Γr)值越大，模糊递增的程度越大.

求出Γ1，Γ2，…，Γp区间之间模糊递增依赖隶属函数的最小值，作为条件属性相对决策属性依区间划分Ψ的递增程度，或说依区间划分Z的递增程度.如果隶属函数最小值为0，那么认为相对D'依区间划分Ψ没有递增，或说依区间划分Z没有递增.由区间划分及定义2可以得出命题2.

命题2如果Γ1，Γ2，…，Γp区间之间模糊递增依赖隶属函数存在不等于0的最小值，那么该最小值必然是在相邻的两个区间之间产生的.

证明假设1≤i＜j≤p，j≠i+1，μ(Γj，Γi)≠0，并且μ(Γj，Γi)是Z划分的最小值，则存在i＜k＜j，μ(Γk，Γi)≠0，μ(Γj，Γk)≠0⇒minΓj≥minΓk，从而推出μ(Γk，Γi)≤μ(Γj，Γi)，因此假设不成立，最小值必然在相邻的两个区间之间产生，记为，表示条件属性集合依Z划分所得的模糊递增程度，也称为D'依Ψ划分依赖于的模糊递增程度，得出文中所需要定义的决策属性与条件属性的模糊递增依赖关系.

2.3 模糊递增依赖关系的参数及性质

关于区间划分个数p的讨论，如果每个区间只有一个元素，就变成了研究严格单调递增依赖关系，从而失去了模糊意义，如果把所有元素作为一个区间也会失去研究意义.如果决策属性与条件属性之间确实是单调递增关系，那么可以认为由于干扰和误差等因素的影响，没有出现严格单调递增关系，而是出现了模糊单调递增关系.这些影响因素的作用是在一定范围内的，往往在数值相近的决策属性值之间映射到条件属性值后，条件属性值没有表现出严格单调递增情况;这种误差也是在一定范围内，一定范围的误差在一个小区间内时，对该区间会产生较大的影响，而当放到一个大的区间内，产生的影响明显较小.按照这样的思路，前面定义的模糊递增隶属函数值会随着区间数p的减小及单个区间范围的增大而出现大于等于原来值的趋势，当然中间可能出现波动，如果出现波动，文中称误差在该区间范围内作用是不稳定的;当p减小到一定值后，由于误差的作用稳定变小，模糊递增隶属函数值会随p的减小而稳定地大于或等于前面的值，这时可称误差在该范围内的作用是稳定的.当p=1时，模糊递增隶属函数因为缺少比较对象而失去作用.由以上分析得到命题3.

命题3当p为偶数且大于等于4时，如果模糊递增隶属函数值不为零，那么以p/2个数进行Ψ划分所得的模糊递增隶属函数值必然大于等于以p个数进行Ψ划分的模糊递增隶属函数值.

证明设当决策属性集合D'以p个数进行Ψ划分时，可得到决策属性区间集合…，Ωp}，通过映射f，可得Z划分的条件属性区间集合ΓCi={Γ1，Γ2，…，Γp}，当决策属性集合D'以p/2个数进行Ψ划分时，可得决策属性区间集合，通过映射f，可得Z划分的条件属性区间集合.根据前面的定义，由于p为偶数，容易得当1≤k≤p/2－1时设α∧β∧γ.当α≤β≤γ时由于模糊隶属函数值不为0，可得minΓ2k+2≥minΓ2k+1≥minΓ2k≥minΓ2k－1，那么有

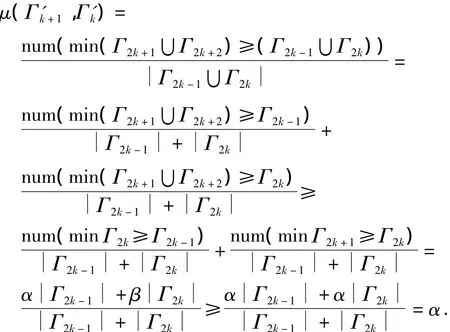
根据命题3和前面的分析，可得出命题4.

命题4如果决策属性确实模糊单调递增依赖于条件属性，那么模糊单调递增隶属函数必然是在p=2或p=3时取得最大值;否则，判定决策属性依决策表不能确定模糊单调递增依赖于条件属性.

证明当p=1时，模糊单调递增隶属函数不存在.依命题3，当p=2或p=3时，模糊单调递增隶属函数值必然大于等于p=4或p=6时的值，也大于等于p是2或3的偶数倍时的值.如果决策属性和条件属性确实是单调递增依赖关系，那么出现模糊单调递增而不严格单调递增的原因是受到了干扰因素的影响，如果它们之间的单调递增依赖关系较强，那么受干扰的影响会较小，否则会较大.

一定的干扰因素在小范围内的影响明显大于在大范围内的影响，但当p=2时模糊单调递增隶属函数值并不一定大于等于p=3时的值，这是因为两个划分单个区间的范围可能相差不是很大，而受干扰的元素在区间中的分布不均匀，划分的区间中心点位置不一样.在命题3中，p/2所划分的区间中心点明显包含在p中，p=2时的模糊单调递增隶属函数值大于等于p=3时的值是大概率事件，因此如果p=5时的模糊单调递增隶属函数值大于p=2或p=3时的值，而p=5时所划分的单个区间范围小于p=2时所划分的单个区间范围的一半，那么只有两种可能:(1)决策属性并非单调递增依赖于条件属性;(2)决策表中受干扰的元素过多或者决策属性和条件属性之间的单调递增依赖关系不明显或强度不够.由此可判定决策属性依决策表不能确定模糊单调递增依赖于条件属性.

综合上述分析可得出如下结论:p的值从k'(k'＜n)开始逐渐变小至2时，如果模糊递增隶属函数的值不等于0，且后面的隶属函数值大于等于前面的隶属函数值，当p=2或p=3时隶属函数值最大，则可以认为模糊递增隶属函数值从p=k'开始是稳定增大的，且干扰误差在范围内是稳定的，决策属性D与条件属性Ci是模糊单调递增依赖的，模糊单调递增程度取决于模糊递增隶属函数值，否则是不单调递增依赖的.

2.4 算法的步骤

1)用二维数组存放决策表D［n，m+1］，其中第m+1列为决策属性，第1至m列为条件属性.

2)对决策属性按从小到大的顺序进行排列，交换相应的行，即对第m+1列的值按从小到大排序，交换对应的行.

3)考察第i个条件属性值与决策属性值的模糊单调递增依赖关系.{Selectp＜n;

for(L=pto 2)

{初始化存放模糊单调递增隶属函数的数组;

求区间距离和区间中心点;

forv=1 ton∥划分区间，并求相应的隶属函数{映射到条件属性i，并划分区间;

forw=1 toL－1

{求相邻区间的隶属函数值;

求这次划分的隶属函数值;}}}}4)判断是否是模糊单调递增关系，求出最大的模糊隶属函数值及其对应的索引号.

5)求出p→2过程中模糊单调递增隶属函数值开始稳定递增的p值.

6)求出干扰因素的稳定作用范围.

该算法的时间复杂度主要集中在步骤2)的排序和步骤3)中，由于步骤3)存在三重循环，因此算法的时间复杂度为O(n3).

3 算法在污水处理中的应用

采用文中算法对UCI的污水数据［17］进行挖掘，找出与输出因素有模糊单调递增关系的输入因素及其依赖程度，从而通过控制输入来达到控制输出的目的.由于UCI污水数据中存在不完备的数据，因此文中先过滤掉不完备的数据，提取出完备的决策表，得到246×38的完备数据信息表.其中样本数据对象个数为246，对象属性个数为38，前22个属性为对象的输入数据属性(文中将它们作为决策表的条件属性)，第23至29个属性为对象的输出数据属性(文中将它们作为决策表的决策属性).第24个数据属性DBO-S是污水处理输出的一个重要考察指标，文中把它作为唯一的决策属性，考察22个输入的条件属性与该决策属性的模糊单调递增依赖关系.由于有一个样本数据的DBO-S值是其它样本数据的3倍，因此文中把该样本作为噪声样本过滤掉，剩下245个样本数据.采用前面的模糊递增函数和文中算法通过Matlab进行仿真计算，部分结果如表1所示.其中当模糊单调递增依赖函数取最大值时参数ε设为0.1，表1中列出的条件属性模糊单调递增依赖函数最大值大多大于0.1，第21个属性SED-D除外，但该属性体现了模糊递增隶属函数的最大值也可能出现在p=3时.

从表1中可以发现，文中算法的仿真结果与前面的理论分析结果相一致，表明输出的生物需氧量与输入工厂的生物需氧量、化学需氧量和悬浮固体有模糊递增依赖关系，并与一沉池的输入生物需氧量和沉淀物、二沉池的生物需氧量和悬浮固体有模糊递增依赖关系，依赖程度为μmax，而其它的条件属性与决策属性不存在明显的模糊递增依赖关系，因此通过控制这些量的输入即可达到控制输出生物需氧量的目的.很明显，文中算法还可以应用于其它工业和社会决策表的数据挖掘，并产生相应的控制策略.

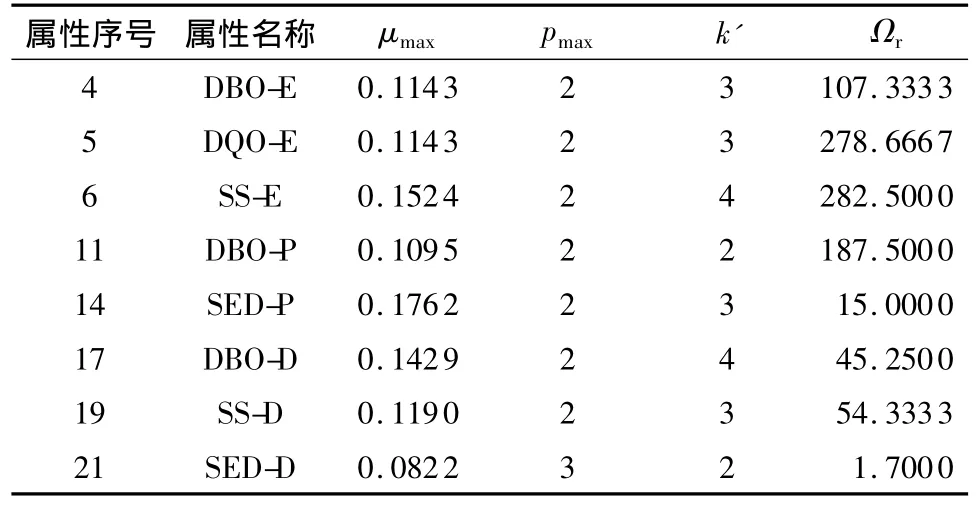
表1 DBO-S与条件属性的模糊单调递增依赖关系1)Table 1 Fuzzy monotone increasing dependent relationship between DBO-S and condition attributes

4 结语

在模糊粗糙决策表的理论基础上，文中提出了基于决策表的模糊粗糙单调算法.首先通过区间映射定义了模糊单调依赖关系的概念，讨论了模糊单调递增依赖关系的参数及性质，并证明了相关命题，然后将该算法应用到污水处理中，取得了良好的效果.文中算法通过模糊单调关系挖掘出对决策输出的变化有重要影响的条件输入属性，等价关系等已有方法不容易在输入与输出之间建立模糊单调关系，而模糊单调关系在复杂的输入输出环境中比等价关系和严格单调关系更加普遍，因此文中算法是对模糊粗糙集理论的丰富和发展，改善了已有方法不容易在输入与输出之间建立模糊单调关系的局限性，今后将进一步完善文中算法，并将其应用于医疗(如检查某药物对某些症状的治疗效果)等其它方面.

［1］Pawlak Z.Rough sets［J］.International Journal of Computer and Information Sciences，1982，11(5):341-356.

［2］Zadeh L.Fuzzy sets［J］.Information and Control，1965，8(3):338-353.

［3］Polkowski L，Skowron A，Zytkow J.Rough foundations for rough sets［M］∥Lin T Y，Wildberger A M.Soft compu-ting:rough sets，fuzzy logic，neural networks，uncertainty management，and knowledge discovery.San Diego:Society of Computer Simulation，1995:142-149.

［4］Lin TY.Neighborhood systems and approximation in relational databases and knowledge bases［C］∥Proceedings of the Fourth International Symposium on Methodologies of Intelligent Systems(Poster Session).Charlotte:Oak Ridge National Laboratory，1989:75-86.

［5］Greco Salvator，Matarazzo Benedetto，Slowinski Roman.Rough sets theory formulticriteria decision analysis［J］.European Journal of Operational Research，2001，129(1):1-47.

［6］Dubois D，Prade H.Rough fuzzy sets and fuzzy rough sets［J］.International Journal of General Systems，1990，17(2/3):191-209.

［7］Wu C J.Guaranteed accurate fuzzy controllers formonotone functions［J］.Fuzzy Sets and Systems，1997，92(1):71-82.

［8］Chou Te-shun，Lee Edward T.Fuzzy monotone functions and applications［C］∥Proceedings of IEEE International Conference on Fuzzy Systems，IEEE World Congress on Computational Intelligence.Anchorage:IEEE，1998:829-834.

［9］Van Broekhoven Ester，De Baets Bernard.Monotone Mamdani-Assilian models under mean of maxima defuzzification［J］.Fuzzy Sets and Systems，2008，159(21):2819-2844.

［10］Grigorenko Olga.Degree of monotonicity in aggregation process［C］∥Proceedings of IEEE International Conference on Fuzzy Systems.Barcelona:IEEE，2010:1080-1087.

［11］Van Broekhoven Ester，De Baets Bernard.Only smooth rule bases can generate monotone Mamdani-Assilian models under center-of-gravity defuzzification［J］.IEEE Transactions on Fuzzy Systems，2009，17(5):1157-1174.

［12］Seki Hirosato，Ishii Hiroaki，Mizumoto Masaharu.On the monotonicity of fuzzy-inference methods related to T-S inferencemethod［J］.IEEE Transactions on Fuzzy Systems，2010，18(3):629-634.

［13］Ye Mingquan，Wu Changrong.Decision table decomposition using core attributes partition for attribute reduction［C］∥Proceedings of the 5th International Conference on Computer Science＆Education.Hefei:IEEE，2010:23-26.

［14］Zhang Shuhong，Sun Jianxun.Continuous value attri-bute decision table analysis method based on fuzzy set and rough set theory［C］∥Proceedings of the Sixth International Conference on Fuzzy Systems and Knowledge Discovery.Tianjin:IEEE，2009:75-79.

［15］张文修，吴伟志，梁吉业，等.粗糙集理论与方法［M］.北京:科学出版社，2001:19-30.

［16］陈水利，李敬功，王向公.模糊集理论及其应用［M］.北京:科学出版社，2005:2-23.

［17］Frank A，Asuncion A.{UCI}machine learning repository［DB/OL］.(1993-06-01)［2010-10-01］.http:∥archive.ics.uci.edu/ml/datasets/Water+Treatment+Plant.