二端变类器实现忆阻元件

王清华，宋卫平

（太原科技大学 电子信息工程学院，山西 太原 030024）

0 引言

基本电路理论中，常见的基本电路元件有：电阻、电感、电容。这些元件的特性是用电压、电流、磁链和电荷这4个物理量来表征。1971年，蔡少棠（L.Chua）先生指出应该有六个数学关系来联接这四个基本的物理量。但现在只有五个确定的关系，从对称的观点看，推测出有第四种基本元件存在，他称为忆阻器（M），用来反映电荷和磁链之间的函数关系［1］。2008年惠普实验室的 Williams等人［2］成功的在纳米尺度下制作出了具有忆阻特性的器件，从而证明了蔡少棠推测是正确的。

变类器是线性二端口类型变换器的统称。它的作用是把电路元件从一种类型转变为另一种类型。一般变类器可用有源元件综合而成。利用变类器可以用四种基本二端元件电阻、电感、电容、忆阻中的任意一种来实现其他三种。本文通过对忆阻元件特性的分析，根据二端口网络理论，给出了将非线性电阻通过变类器转换成忆阻元件的电路模型。

1 忆阻元件的特性

由电磁场理论知道，电压、电流、磁链和电荷之间存在着下述关系：

可见，上述两对变量之间是动态相关的［3］。对于任何元件，这两对变量均由式（1）联系在一起，而与元件的性质无关。四个变量的六对组合中，（u，i），（i，φ），（u，q），（Ψ，q）这四对变量之间的关系是用来确定元件性质的，我们称它们两两之间动态无关。这四对变量定义电阻元件（u，i）、电感元件（i，Ψ）和电容元件（u，q）中，有一对动态无关的变量偶（Ψ，q）未被使用。蔡少棠从电路变量关系完整性角度，定义了增量忆阻来描述（Ψ，q）之间的关系。

［4］给出的电阻器、电容器和电感器的定义，根据电路理论来介绍忆阻器的一般定义。

［定义1］一个二端元件，当且仅当在任一瞬间t，电荷q与磁链Ψ两者之间的关系是由Ψ～q平面上的一条曲线来决定的。此二端元件为忆阻器。

上述在Ψ～q平面上的特性曲线所表达的关系，称为忆阻器的构造性关系。这条曲线是忆阻器在时间t的特性曲线，确定了时间t时电路变量Ψ（t）和q（t）的全部可能的数值集合。可用代数方程f［Ψ（t），q（t），t］＝0来表示上述特性曲线。忆阻器构造性关系的另一数学表达法为

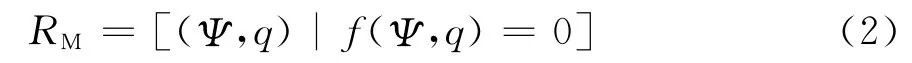
忆阻元件分为流控型和压控型［5］。

流控忆阻元件的端口方程为

式中，M（q）＝dΨ／dq称为流控忆阻元件的增量忆阻，M（q）的量纲与电阻相同。

压控忆阻元件的端口方程为

式中，W（Ψ）＝dq／dΨ具有电导的量纲称为链控忆阻元件的增量忆导。W（Ψ）的值与碰链Ψ有关，取决于电压从 －∞ 到t的积分。即W（Ψ）可以记忆元件端电压的值。

蔡少棠指出虽然忆阻器的定义涉及磁通量，但磁场并不能直接对忆阻器起作用。电流的定义是电荷量对时间的求导，根据法拉第定律电压是磁通量对时间求导。因此，仅需要在电流的积分和电压之间有一个非线性关系即可反映忆阻元件［6］。

2 忆阻元件的实现

变类器是一族线性二端口类型变换器的统称。它的作用是把电路元件从一种类型转变为另一种类型（如图1）。利用变类器可以用四种基本二端元件R、L、C、M中的任意一种来实现其他三种。特别有意义的使用电阻器和变类器来实现忆阻元件。实际上，我们也是使用黑箱方法根据忆阻器的外部特性进行造型。

图1 变类器结构

如果要把一个电阻元件变换为一个忆阻元件，则应使表征电阻元件的i－u特性曲线上的每个点，映射成那些用来表征忆阻元件的Ψ～q特性曲线上的相应点，如图2所示。

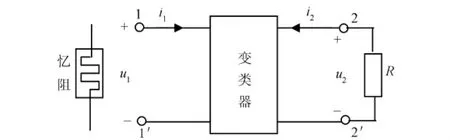
图2 R－M变类器结构

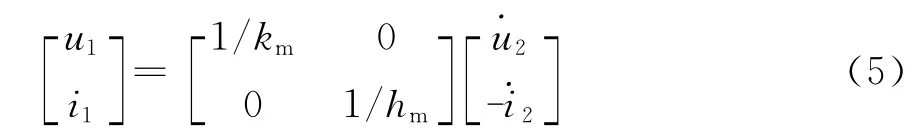
［定义2］一个二端口元件，如果它在任一瞬间t的端口电压u1和u2，端口电流i1和i2符合式（5）所表达的构造性关系，则称为第Ⅰ型R－M变类器。

将电阻元件变换成为一个忆阻元件的另种方法是使R－M 变类器的中间作用为u2q1，（－i2）Ψ1，可得状态方程：

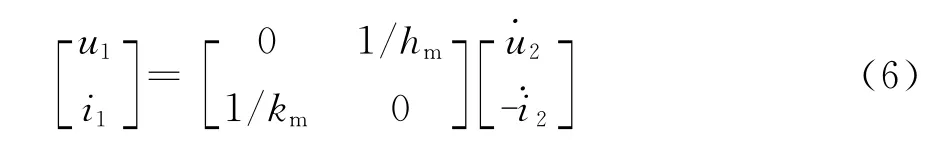
由上式可知，u1取决于i2的变化率，i1取决于u2的变化率，u1和i1的比值等于增量忆阻M（q）。

［定义3］一个二端口元件，如果它在任一瞬间t的端口电压u1和u2，端口电流i1和i2符合式（6）所表达的构造性关系，则称为第Ⅱ型R－M变类器。

根据式（5）可以得出第Ⅰ型R－M变类器电路原理图，用T型网络表示；根据式（6）可以得出第Ⅱ型R－M变类器的电路原理图，用双倒L型网络表示。如图3和图4所示。图中涉及的线性电容、电阻、电感及受控源均能用现有的器件实现，由这些器件实现的忆阻器为有源器件。

图3 第I型R－M变类器电路原理图

图4 第II型R－M变类器电路原理图

3 结语

本文在讨论忆阻元件的基础上，介绍了利用二端变类器实现忆阻元件的端口特性方程，并将电阻元件通过M－R型变类器转换成忆阻元件，给出了电路模型图。我们也可以使用同样的方法得出M－C和M－L型变类器。将电容元件或电感元件通过变类器得到忆阻元件，从而得到了由电子器件组成的有源忆阻器。

参考文献：

［1］L.O.Chua.Memristor －the missing circuit element［J］.IEEE Trans.On Circuit Theory，1971，18（5）：507－519

［2］D.B.Strukov，G.S.Snider，D.R.Stewart，and R.S.Williams，“The missing memristor found，”Nature 453，80－83（2008）

［3］刘小河.非线性电路理论［M］.北京：机械工业出版社.2009

［4］林争辉.电路元件的映射理论［J］.上海：上海交通大学学报，1995，29（1），54－60

［5］俎云霄，于歆杰.忆阻元件的研究进展［J］.南京：电气电子教学学报，2010，32（6）

［6］Frank Y.Wang.Memristor for introductory physics.arXiv：0808.0286v1 ［physics.class－ph］4Aug 2008