基于多幅图像平均法对数字图像降噪的研究★

马艳娥，陈思，陈娟，刘妍，姚金杰

（中北大学 信息探测与处理技术研究所 太原 030051）

0 引言

在实际获取和传输图像的过程往往会发生图像失真，所得到图像和原始图像有某种程度的差别。这些都是因为有外界的噪声加入到图像中，因此在对采集到的图像进行处理前，需要先对图像进行预处理，就是要对噪声图像进行滤波，平滑噪声图像。传统的降噪方法有中值滤波、均值滤波、维纳滤波[1-2]等，这些方法对于非平稳过程信号有着明显的局限性。

多幅图像平均法[3]处理常用于摄像机的视频图像中，用以减少电视摄像机光电摄像管或CCD器件所引起的噪声，这是对同一景物连续摄取多幅图像并数字化，再对多幅图像平均，它能更准确地得到图像上特征信息。

1 多幅图像平均法的原理

多幅图像平均法是对同一景物重复采集M次相加后取平均值的方法来消除噪声的。 图像成像的模型[4]可描述为：

其中，f(x,y)是不含噪声的理想图像，g(x,y)是有噪声图像， ( x , y ) 为噪声。

若噪声是每一坐标(i,j)点无关的，且其数学期望为零，则g(i,j)的期望值为：

M幅重复采集的图像平均后的输出图像为：

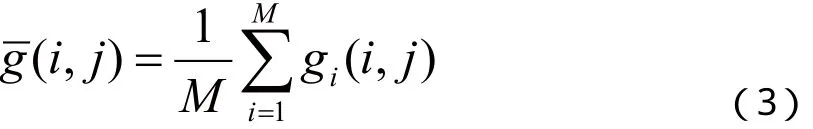
且平均后输出图像的方差为：

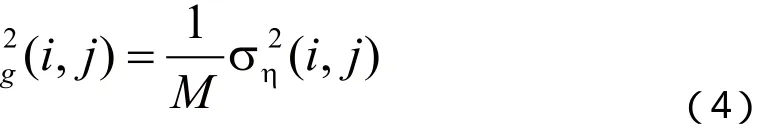
本算法的流程图如图1所示。

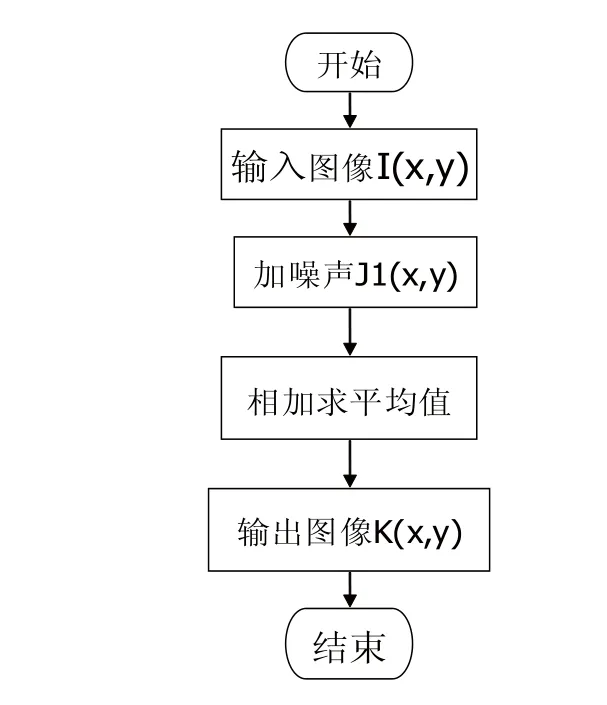
图1 多幅图像的算法流程图

2 实验结果分析

为了验证本文提出法的算法的有效性，设计了2组实验。这2组实验分别利用MATLAB7.0工具对多幅图像平均法进行实现。

第1组实验通过对标准的端子图像为例来进行说明和分析。对图像加椒盐噪声[5]，利用被噪声污染端子图像作为输入，图2大小为225*255，灰度级为256的原图像，图3加入密度为0.04的椒盐噪声图像，图4-7分别是中值滤波，均值滤波，维纳滤波均采用3*3模板降噪结果图，图6多幅图像平均法是取100幅加有噪声的图像进行降噪后的结果图。

图2 原始图像

图3 加椒盐噪声图

图4 中值滤波图像

图5 均值滤波图像

图6 维纳滤波图像

图7 多幅图像平均法

从图像直观来看，对于椒盐噪声，中值滤波降噪效果比均值滤波好，多幅图像平均法是效果最好的。采用常用的客观评价指标的参数[7-8]有峰值均方误差（RMSE），峰值信噪比（PSNR)来定量进行比较。

均方误差的表达式为：

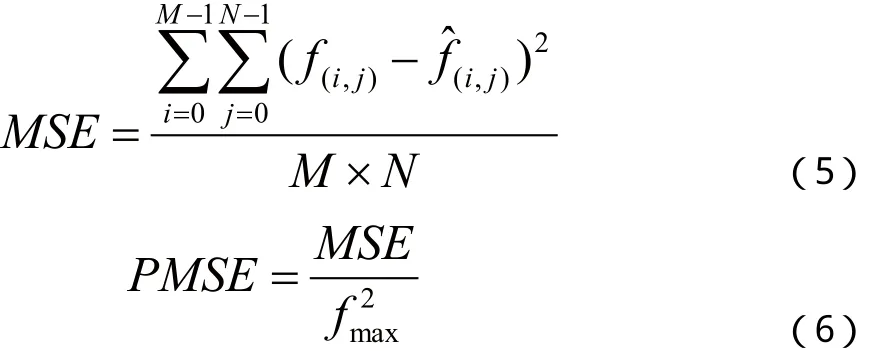
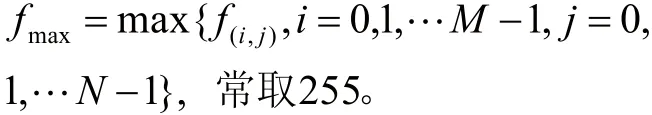
PSNR本质上与MSE相同，其表达式为：

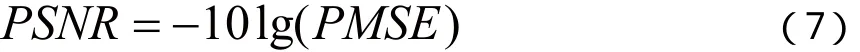
对于端子图像加椒盐噪声后各算法输出图像，计算其客观评价指标如表1.从表1中可以看出，中值滤波的峰值信噪比最低，对椒盐噪声的降噪效果不及其它几种算法，多幅图像平均法的峰值均方误差最小，有较好的降噪效果。

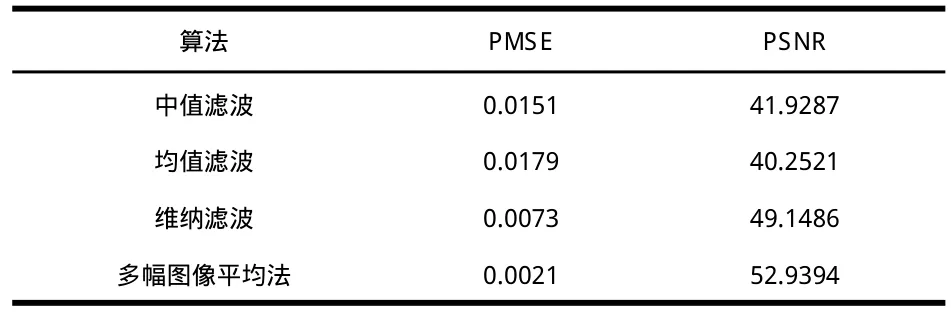
表1 椒盐噪声各算法输出图像指标比较

第2组实验为了进一步比较算法对不同噪声的适用性，通过对标准的Lena图像加均值为0.1，方差为0.02的高斯噪声[6]来比较本文提出的多幅图像平均法和传统几种算法之间的优异性，结果如图8-图13所示。

图8 原始图像

图9 加高斯噪声图

图10 中值滤波图像

图11 均值滤波图像

图12 维纳滤波图像

图13 多幅图像平均法

从主观上看，对于高斯噪声，均值滤波的效果好于中值滤波，而维纳滤波滤除效果比均值滤波好，但没有保留原图像的细节信息，不如多幅图像平均法。再采用客观的评价指标，分别计算对Lena图像加椒盐噪声和高斯噪声，经过几种降噪后输出图像的客观评价指标值，见表2，表3：

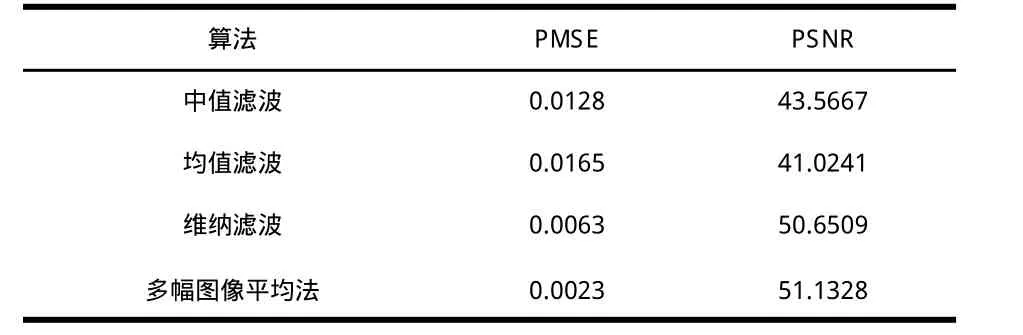
表2 加椒盐噪声后各算法指标比较

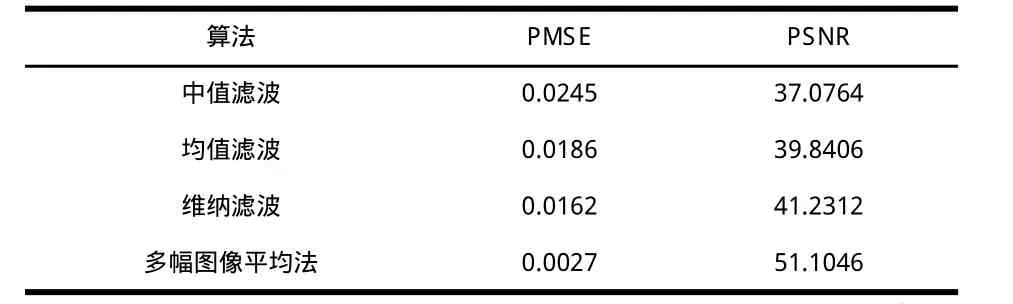
表3 加高斯噪声后各算法指标比较

从表2可以看出,对于椒盐噪声，仍然是均值滤波的峰值信噪比最低，多幅图像平均法的峰值均方误差最小，这与表1的情况一致。所以，对于椒盐噪声的降噪效果不太理想，而多幅图像平均法则取得较好的效果。而从表3中，看出中值滤波的峰值信噪比最低，多幅图像平均法的均方误差仍为最小。

3 结论

本文论述了多幅图像平均法降噪的原理，并在MATLAB中和传统的算法进行了比较，在有椒盐噪声和高斯噪声的条件下，比较结果显示多幅图像平均法要优于传统其它算法，可以很好的达到数字图像降噪效果。然而，本算法仍然会丢失部分边界纹理信息，减少边界纹理信息细节特征的丢失将有待进一步深入研究。

[1] 郭琳,尚振红.一种有效地自适应中值滤波算法[J].长春工业大学学报,2008,29 (1):87-90.

[2] 李世进.数字图像的平滑处理[J].湖南科技学院学报,2008,1(29):23-24.

[3] 张旭明,徐滨士,董世运.用于图像处理的自适应滤波[J].计算机辅助设计与图形学学报,2005(2):295-299.

[4] 李慧娜,平源.有效去除图像混合噪声的方法[J].计算机工程与设计,2008,7(29) :36-38.

[5] Coyle E J,GabboujM,Lin J H.1991,From M e d i a n F i l t e r s t o O p t i m a l S t a c k Filtering[J].IEEE Internet Symp.Ci- rcuits Systems,1991（1）:9-12.

[6] Rudin L I,Osher S,Fatemi E.Nonlinear Total Variation Based Noise Removal Al-gorithms[J]. physica,1992,60:259-268.

[7] 牛轶峰,赵搏欣.像素级图像优化融合客观评价指标分析[J].计算机与数字工程,2010,3(38):116-121.

[8] 刘洁瑜，徐军辉，汪立新.基于结构信息分布的图像质量评估新算法[J].兵工学报,2010,8(31):1054-1058.