时变海面复反射系数建模

李晓飞 许小剑

(北京航空航天大学 电子信息工程学院,北京 100191)

时变海面复反射系数建模

李晓飞 许小剑

(北京航空航天大学 电子信息工程学院,北京 100191)

基于二维时变海面模型和粗糙面电磁散射的低阶小斜率近似方法,研究了海面复反射系数的时变和统计特性.在电磁散射幅度基础上推导了粗糙面反射系数及其相干和非相干分量,相干分量理论计算公式与经验模型一致.仿真结果表明相干分量幅度与经验模型基本吻合,但相位中存在明显的起伏特性,这种起伏在经验公式中没有体现出来.引入 Middleton相位差统计模型为反射系数时变特性建模,仿真数据统计与理论分布吻合较好,且概率密度函数的等高图可以很好地表征时变复反射系数间的相关特性.这种吻合性表明复反射系数在短时间尺度上满足高斯分布,但其幅度和频率被海浪长波调制.

粗糙海面;复反射系数;电磁散射;统计分布

在海上船用雷达系统中,雷达的接收信号受到动态海面反射的影响.基于舰船-海背景电磁耦合作用的复杂性,高频近似方法以其较快的速度和较好的精度而被广泛采用[1-2],它通过粗糙面反射系数来引入非直接路径的贡献.研究动态海面的反射系数特性对解决该多径散射问题有着重要的意义.

传统上采用的相干反射系数经验模型是在菲涅尔反射系数的基础上加入指数项衰减因子来计入粗糙度的影响[2-3],与实测数据吻合较好,在海上目标电磁散射建模中应用广泛.而考虑一个随海浪运动的时变系统,这种简单的经验模型是不够的,要获得准确的海上目标回波的动态特征,需要一个能够计入海面几何结构、随机特征和时变特性等因素影响的反射系数模型,能够表征反射系数随海面运动的变化特性,能够揭示其统计意义.基于此需求,本文考虑采用粗糙面电磁散射模型为时变海面复反射系数建模.

解决粗糙面电磁散射问题的方法可分为数值方法和近似方法两大类.后者在减小计算量上具有明显的优势,能够满足时变海面蒙特卡洛仿真的需求.其中,小斜率近似方法(SSA,Small Slope Approximation)是在微扰法(SPM,Small Perturbation Method)和基尔霍夫近似(KA,Kirchhoff Approximation)的基础上发展起来的,计算精度较高,在小擦地角时与实测数据吻合较好,是一种计算粗糙面电磁散射的有效方法[4-5].

本文重点关注动态海面复反射系数的时变特性和统计特征.采用低阶 SSA方法为粗糙面反射系数建模,推导其相干和非相干分量,通过蒙特卡洛仿真与经验模型进行对比和分析,研究该建模方法对多径散射计算的影响.为了更好地表征复反射系数的时变特性,引入 Middleton相位差统计模型[6].文献[7]曾将该模型应用于海面实测后向电磁散射数据.就作者所知,本文首次引入Middleton分布模型为海面时变复反射系数相关特性进行建模,所得结论对后续研究有一定的指导意义.

1 动态海面模拟

获取海面的时变电磁散射信号需要预知准确的粗糙面信息.设定时间间隔对动态海面进行离散,计算每一帧“静止”海面的电磁散射就可以得到时变的场序列.该过程需要海面的随机信息、相关特性(海谱)和随时间变化的水动力学关系.

本文将海面建模为符合 PM(Pierson-Moskowitz)海谱的高斯随机过程.二维 PM谱定义为波数和方位角的函数[8]:

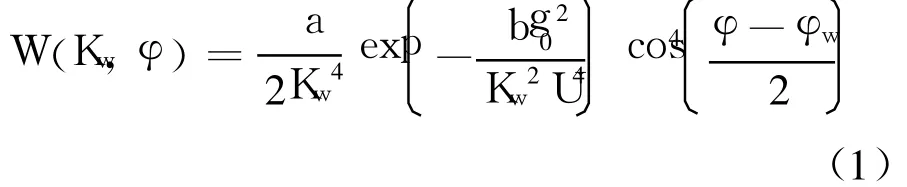
其中,g0=9.81m/s2是重力加速度常数;Kw是海浪的空间波数;常数 a=8.10×10-3,b=0.74;U是海平面上空 19.5m处的风速.方位角 φ和风向角 φw分别定义为海浪波数矢量和风速矢量在 x-y平面内与 x轴正向的夹角.

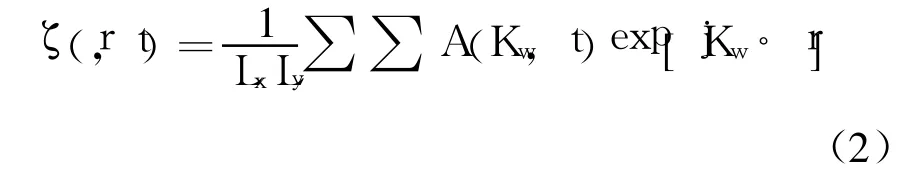
其中

图1给出了逆风向、风速分别为 3m/s和5m/s时海面高度值的概率密度分布曲线,并与理论高斯模型进行比较.可以看出,基于谱方法得到的海面高度值接近高斯分布,但略有偏离,风速变大,该偏离程度有所增加.

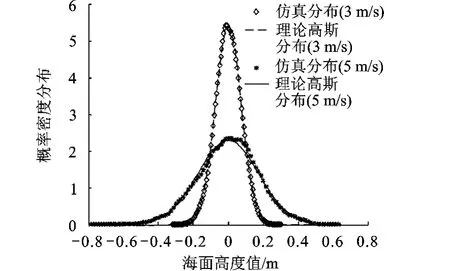
图1 海面高度值概率密度分布及相应的理论高斯曲线

2 复反射系数计算

2.1 散射幅度表示

考虑一均匀平面波从 z＞0的空间照射到海面上,二维粗糙面电磁散射如图 2所示.则入射波矢量为其中,k0和 -q01分别为其水平和垂直分量,为入射波波数;散射波矢量为其中,k和 q1分别为其水平和垂直分量,

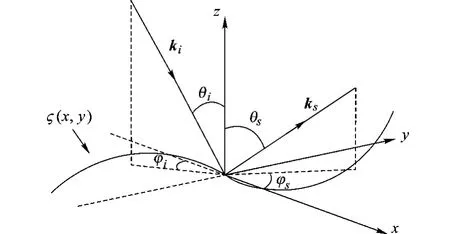
图2 二维海面散射几何示意图

基于低阶 SSA方法,散射幅度可由下式得到:

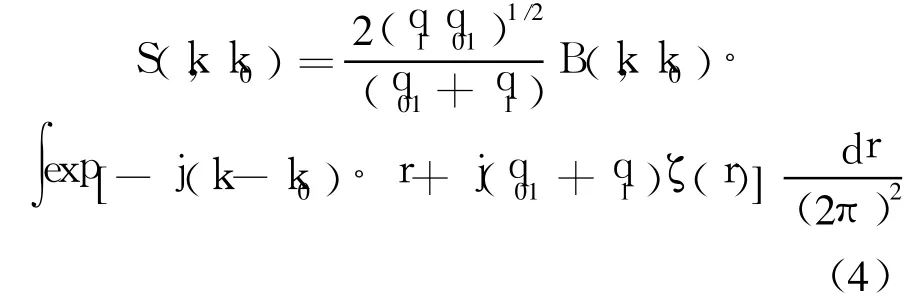
对于介质海面,散射矩阵幂级数展开系数可以表示为

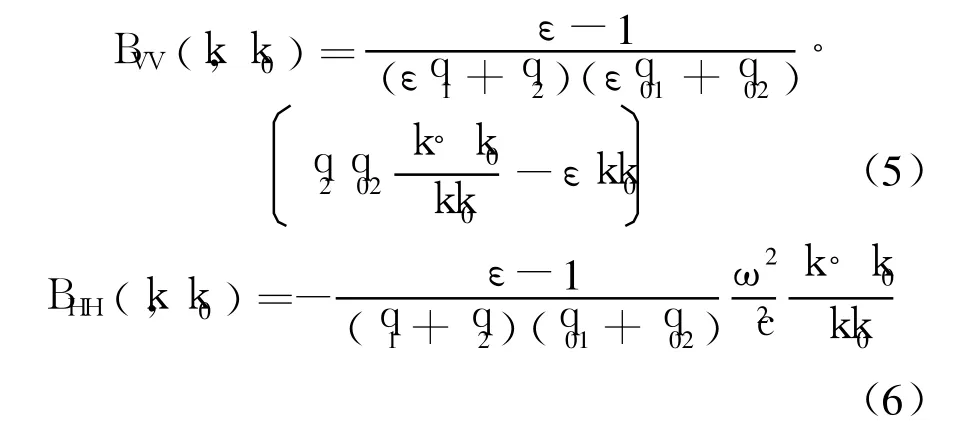
其中,q02,q2为介质中的垂直波矢[4],海面复介电常数 ε可由 Debye公式[10]得到.

2.2 复反射系数及其相干和非相干分量

设定入射波方位角为 φi=0°,对于镜面反射方向,有 θs=θi,φs=0°,即 k=k0.则有

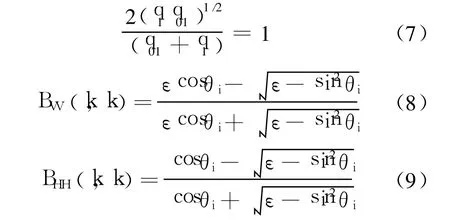
可见,系数 B即为菲涅尔反射系数 Γ[11].

将式(7)～式(9)代入式(4),并对粗糙面截获的入射波能量进行归一化,可以得到粗糙面复反射系数 γ的表达式:

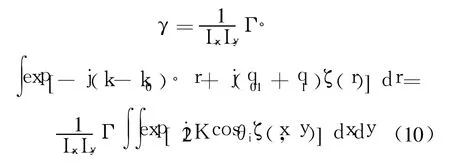
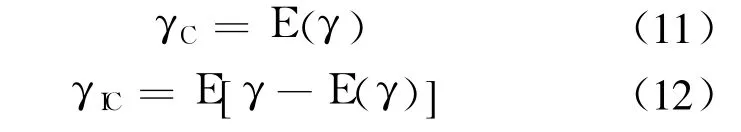
其中 E(·)代表求平均.

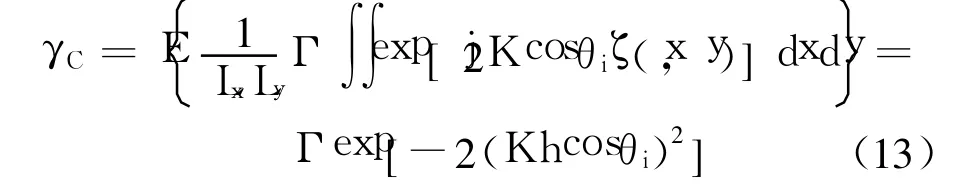
其中 h为海面的均方差高度.该推导结果与一般文献中给出的经验公式吻合[2-3].

3 相位统计分布模型

目前,文献中对海面电磁散射信号的研究多局限于幅度的一阶统计、功率或是它们与环境参数的依赖关系.对于时变信号,更需要了解其调制机理以及不同时间间隔信号的相关性,对此,相位差分布是一个有效的分析工具.

设{γi,i=1,2,…,N}为一组时变复反射系数序列,其相位差定义为 Δφ=Arg(γ*(t)γ(t+τ)),其中 τ为时间间隔.若在短时间尺度上其同相和正交分量满足联合高斯分布,则 Δφ的概率密度函数可表示为[6]

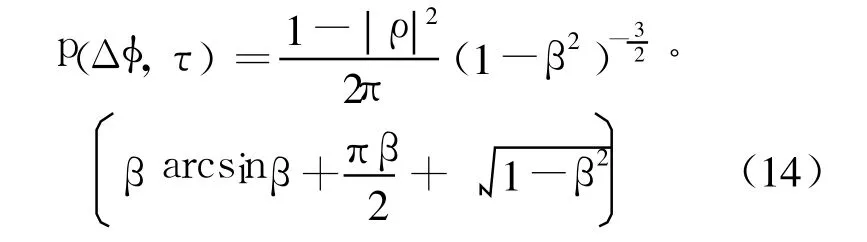
其中

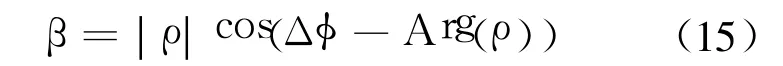
ρ为归一化自相关函数估计,文献[7]对原Middleton模型进行修正,定义 ρ为多段数据自相关函数的均值:

其中,ΔT取值介于相位的去相关时间和海面长波浪的周期值之间.通过式(16)的修正可以移除长波浪对信号幅度的调制.

4 仿真结果分析

设定雷达入射波频率为 1GHz,海面尺寸为60.38m×60.38m,空间采样间隔取 λ/5,其中 λ为入射波波长.海水含盐量为 32.54‰,温度为20℃.

4.1 复反射系数随时间的变化特性

图3分别给出了不同风速下,擦地角 ψ=20°时水平极化复反射系数幅值随时间的变化曲线.从图中可以看到,随着风速的增加,反射系数幅值相对起伏程度增强.

图4给出了复反射系数相位差概率密度分布函数的等高图,并与 Middleton模型进行了比较.仿真数据长度为 30000,各条等高线对应的概率密度值分别为 0.002,0.004,0.008,0.012,0.016,0.020,0.024,0.028和 0.032,较小概率对应较大尺寸的等高线.从图 4中可以看到,仿真得到的复反射系数相位差符合理论分布,且关于零值对称.该吻合性说明在短时间尺度上复反射信号为联合高斯分布,但其幅度和频率受到海面长波浪的调制.该调制作用导致信号逐渐与联合高斯分布偏离.

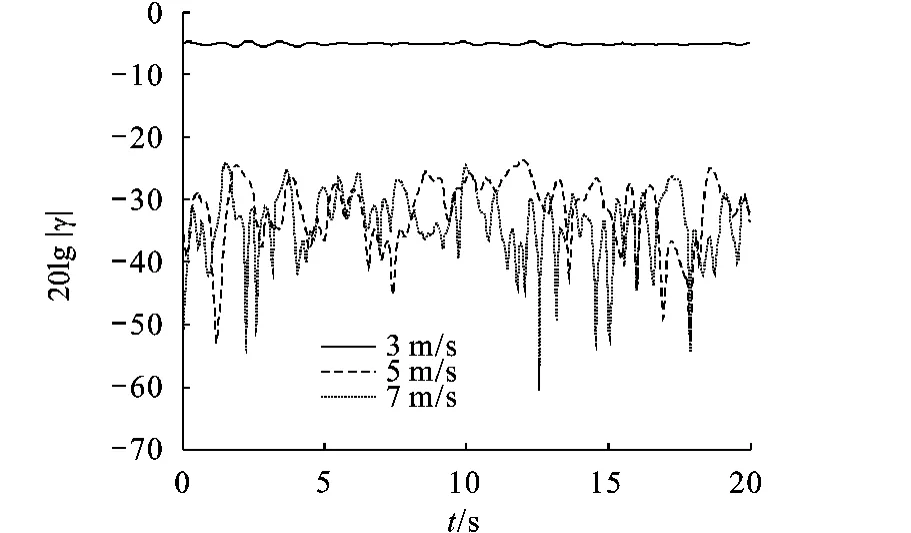
图3 不同风速下反射系数幅值随时间的变化

图4 相位差概率密度分布函数等高图

另外,从等高图上可以很容易看出复反射信号的相关程度.三种情况下,相位去相关时间(即概率密度值为 0.004的等高线最高点所对应的时间间隔)约为:ta＞0.4 s,tb=0.16s,tc=0.32s.可见,风速恒定时,ψ=60°时复反射系数相关性相比 ψ=20°时减弱.限于篇幅,本文没有给出更多的结果,但大量仿真表明,反射系数相关性是随擦地角增大而减弱的.图 4a和图 4c比较可见,时变复反射系数相关性随风速的增加而减弱.

4.2 相干与非相干分量随擦地角的变化特性

风速取 3m/s和 5m/s时,复反射系数相干分量的幅值和相位如图 5所示,蒙特卡洛仿真的次数为1000.

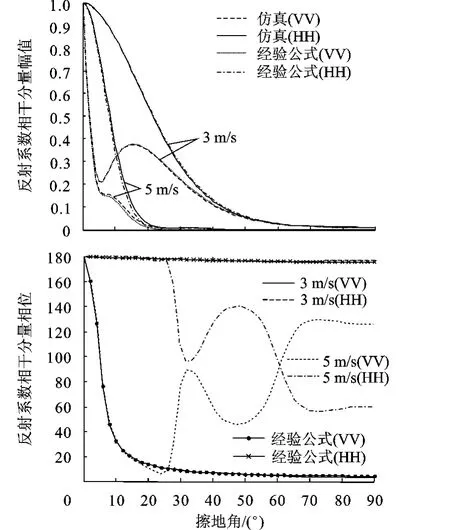
图5 相干反射系数随擦地角的变化曲线以及相应的公式计算结果

从图 5中可以看到,在风速为 3m/s时,Kh≈1,仿真得到的相干反射系数幅值和相位与经验公式计算结果差别较小;但当风速为 5m/s时,Kh≈2.79,相干分量的幅值基本与经验公式吻合,但相位起伏较大.该现象可归结为两个因素的作用:一是随着风速增大,海面高度值与理论高斯分布略微偏离(如图 1所示);二是海面高度值 ζ(x,y)为随机变量,这种非均匀采样在式(10)中叠加求积分时偏离高斯分布特征函数公式,该作用虽然对幅度影响不大,但给相位带来的变化是很明显的.

由式(10)易知,相位起伏程度随表观粗糙度因子 Kh的增大而加剧.但对于较大的 Kh值,复反射系数幅值随擦地角的增大而迅速衰减,因此,这种相位起伏虽然影响雷达接收信号的时变特性,但不会给多径电磁散射计算的统计平均值带来实质性影响.

同图 5相对应的非相干分量幅值如图 6所示,可以看到,随着 Kh的增加,非相干分量曲线变得尖锐,水平极化峰值显著变大,相对于相干分量的比重也随之增加,在 ψ=10°附近,可达到相干分量的 1/10.可见,在 Kh取值较大时,仅采用传统的相干反射系数经验模型来计算多径散射是不够精确的.

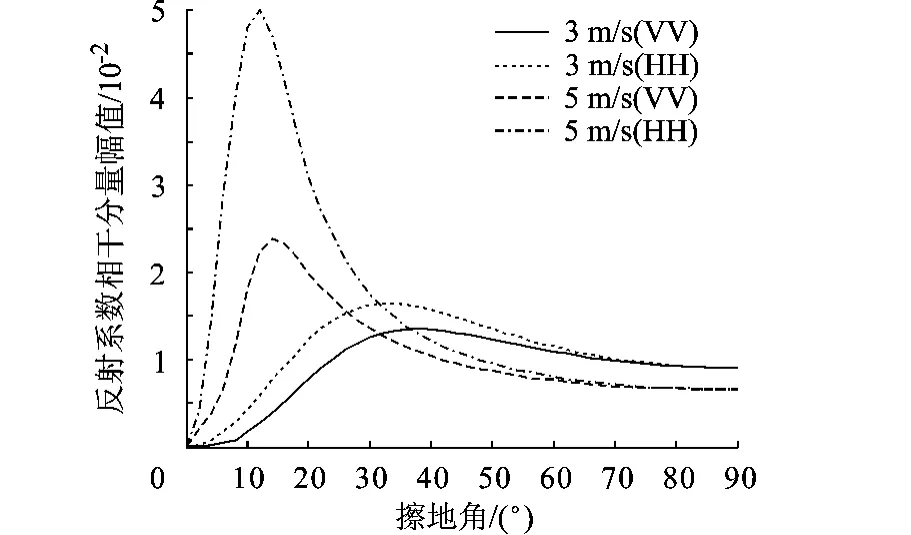
图6 非相干反射系数幅值随擦地角的变化曲线

5 结 论

本文采用低阶小斜率近似方法建立了时变海面复反射系数的计算模型,推导了其相干分量的理论公式,并根据相位差统计分布研究了反射系数的时变特性.

仿真结果表明,海面复反射系数相位差统计与 Middleton模型吻合得较好,说明时变反射系数在短时间尺度上满足高斯分布,其幅度和频率被海浪长波调制;并且,相位差概率密度函数的等高图可以很好地表征时变复反射系数间的相关特性.

另外,蒙特卡洛仿真与经验模型对比发现,相干反射系数的幅度与经验模型计算结果接近,但相位同经验公式的菲涅尔反射系数相位差别很大,尤其是在擦地角较大的情况下.注意到大擦地角条件下,复反射系数幅值较小,这种相位起伏对多径回波的影响通常是有限的,仅在擦地角小于40°～50°时比较明显,在该范围内,海面的非相干反射对多径回波有一定的贡献.

本文的方法和研究结论可用于修正传统的多径散射回波计算模型,提高计算准确度,同时也可用于时变海面目标的多路径动态特性仿真计算.

References)

[1]Shtager E A.An estimation of sea surface influence on radar reflectivity of ships[J].IEEE Transactions on Antennas and Propagation,1999,47(10):1623-1627

[2]Xu X,Wang Y,Qin Y.SAR image modeling of ships over sea surface[C]//SAR Image Analysis,Modeling and Techniques Ⅷ,Proc SPIE.Stockholm,Sweden:[s.n.],2006,V 6363:1-12

[3]Beard C I.Coherent and incoherent scattering of microwaves from the ocean[J].IRE Transactions on Antennas and Propagation,1961,9(5):470-483

[4]Voronvich A G.Waves scattering from rough surfaces[M].Berlin,Germany:Springer-Verlag,1994

[5]Bourlier C,Déchamps N,Berginc G.Comparison of asymptotic backscattering models(SSA,WCA,and LCA)from one-dimensional Gaussian ocean-like surfaces[J].IEEE Transactions on Antennas and Propagation,2005,53(5):1640-1652

[6]Middleton D.An introduction to statistical communications theory[M].New York:McGraw-Hill,1960

[7]Chapman R D,Got wols B L,Sterner R E.On the statistics of the phase of micro wave backscatter from the ocean surface[J].Journal of Geophysical Research,1994,99(8):16293-16302

[8]Toporkov JV,Brown GS.Numerical simulation of scattering from time-varying,randomly rough surfaces[J].IEEE Transactionson Geoscience Remote Sensing,2000,38(4):1616-1625

[9]Rino C L,Crystal T L,Koide A K,et al.Numericalsimulation of backscattering from linear and nonlinear ocean surface realizations[J].Radio Science,1991,26(1):51-71

[10]金亚秋.电磁散射和热辐射的遥感理论[M].2版.北京:科学出版社,1998:61-63 Jin Y.Remote sensing theory of electromagnetic scattering and thermal emission[M].2nd ed.Beijing:Science Press,1998:61-63(in Chinese)

[11]Dawood M,Narayanan RM.Multipath and ground clutter analysis for a UWB noise radar[J].IEEE Transaction on Aerospace and Electronic System,2002,38(3):838-85

(编 辑 :娄 嘉)

Modeling of complex re flection coefficient for time-evolving sea surfaces

Li Xiaofei Xu Xiaojian

(School of Electronics and Information Engineering,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)

Based on the two-dimensional time-varying sea surface model and first-order small slope approximation method,the time-varying and statistical characteristics of complex reflection coefficients from sea surfaces were investigated.In terms of electromagnetic scattering amplitudes,the reflection coefficients and their coherent and incoherent components were derived.The theoretical formula of coherent part is coincident with the empirical model.Simulation results demonstrate that the coherent amplitudes accord with the empirical counterparts,while the phases have unavoidable disturbances,which can not be predicted by empirical formula.Middleton phase difference statistical model was introduced to model the time-varying property of reflection coefficients.The simulated statistics are shown to be in good agreement with the theoretical model,and the contour plots of probability density function can predict the correlation between the complex reflection coefficients adequately.Such agreement suggests that the complex reflection coefficients have a Gaussian distribution on short time scales,but are modulated in amplitude and frequency by the long surface waves.

rough sea surface;complex reflection coefficient;EM scattering;statistical distribution

TN 011

A

1001-5965(2011)02-0197-05

2009-12-10

国家安全重大基础研究 973计划资助项目

李晓飞(1983-),女,河南南阳人,博士生,lxf3294@163.com.