基于 S型测试工作量函数的软件可靠性增长模型

李秋英 李海峰 陆民燕 王学成

(北京航空航天大学 可靠性与系统工程学院,北京 100191)

基于 S型测试工作量函数的软件可靠性增长模型

李秋英 李海峰 陆民燕 王学成

(北京航空航天大学 可靠性与系统工程学院,北京 100191)

软件测试工作量随时间的变化情况对于软件可靠性增长曲线的形状具有显著影响,因此将测试工作量函数(TEF,Testing Effort Function)引入软件可靠性增长模型(SRGM,Software Reliability Growth Model)中以提高软件可靠性评估性能.分析了软件结构特征及学习因素对实际测试过程的综合影响,研究增长速率为先增后减的 S型增长趋势的 TEF,提出两种 S型 TEF,即延迟 S型 TEF与变形 S型 TEF,并提出考虑延迟 S型 TEF的 SRGM(DSTEF-SRGM)以及变形 S型 TEF的 SRGM(ISTEF-SRGM).在两组真实失效数据集上,进行了这两种 SRGM与经典 SRGM及其它考虑 TEF的 SRGM的对比研究.结果表明,ISTEF-SRGM的模型拟合效果最优,同时验证了该模型具有优越的软件可靠性评估性能及模型适应性.

软件可靠性;测试;可靠性分析;增长;模型

软件可靠性已成为软件发布时用户最为关心的指标之一[1].SRGM(Software Reliability Growth Model)作为软件可靠性评估与预计的主要手段,从上世纪 70年代起,就一直是软件可靠性工程领域最为关注的研究方向之一[2-3].虽然已有部分经典的 SRGM被成功地应用于各类安全关键软件中[4-5],但若能在软件可靠性建模中考虑软件测试过程因素的影响,将会进一步提升现有模型的拟合与预计性能[6-8].

测试工作量被认为是一种重要的测试过程因素[6],是指在测试过程中所消耗的资源,可用人力、执行的测试用例数、CPU时间等信息来度量[9].与日历时间相比,测试工作量对缺陷探测效率的贡献更为直接[10],其随测试时间的变化情况对软件可靠性增长曲线的形状具有显著影响[11].早期 SRGM或不考虑测试工作量,或假设测试工作量随时间的消耗率是常值[1,3,12]显然是不合理的.如何建立准确定量描述测试工作量随测试时间变化情况的测试工作量函数(TEF,Testing Effort Function),进而建立考虑 TEF的 SRGM已成为软件可靠性建模研究的热点之一[6,9,11,13-22].

目前已有的 TEF包括:指数、雷利、威布尔[13]、指数威布尔[14]、泛化指数[15]、Burr[16]、Logistic[6,9,11,23]、泛 化 Logistic[17-18]、Log-Logistic[19]及 Chatterjee学习函数模型[20],在此基础上开展的考虑 TEF的软件可靠性建模研究包括:①结合指数型非齐次泊松过程类(NHPP,Non-Homogeneous Poisson Process)的 SRGM[9,11,13-20];②结合S型 NHPP类的 SRGM[6,21-22];③考虑变点[23-26]、排错情况[21,27-28]及失效类型[29]等因素的扩展模型.其中,第 1种类型的模型最为常见且是其它两类模型的研究基础,因此,本文的研究内容与实例验证均围绕这种结合指数型 NHPP类 SRGM展开,暂不考虑与后两类模型的对比研究.

实际测试过程经常会出现如下情形:初始时测试工作量快速增长,但进行到某一时间点后,由于软件结构以及学习因素等综合影响,测试工作量的增长速率会逐渐变慢并趋于平稳,因此测试工作量随时间的增长速率会呈现出先增后减的 S型增长趋势[11].此时,指数类、威布尔类等TEF显然不再适合.Logistic TEF[11]虽然也是一种 S型TEF,但其初始测试工作量不为 0,与直觉不符;且仅有这一种 S型 TEF对于 TEF及其建模研究是远远不够的.

延迟 S型函数[30]与变形 S型函数[31]是两种经典的 S型函数,适于描述 S型增长趋势,且已被应用于软件可靠性建模研究[30-31].本文首先提出两种 S型 TEF,然后提出两种考虑 S型 TEF的指数型 NHPP类 SRGM(STEF-SRGM),最后将这两种 STEF-SRGMs与若干传统 NHPP类 SRGMs及其它典型的考虑 TEF的指数型 NHPP类 SRGMs进行对比,以验证 STEF-SRGMs在模型评估性能上的有效性与适用性.

1 TEF概述

TEF不但可用于描述测试工作量随时间的变化情况,也是建立考虑 TEF的 SRGM的前提与基础.本节首先介绍现有的 TEF(如表 1所示).其中,W(t)表示时间间隔[0,t]内的累积测试工作量,Wmax表示最终消耗的测试工作量,即 Wmax=W(∞),w(t)是测试工作量在时刻 t的增长速率函数,f(t)是学习因素函数(t的增函数).

对表 1中的 TEF,补充说明如下:

①虽然威布尔类 TEF(表 1的 1～6)具有形式灵活等优点,但其无法很好地描述 S型增长趋势,且当形状参数 m＞3时,威布尔类型的函数会有较明显的峰值现象[11];②Logistic类 TEF(表 1的 7～8)虽然为 S型 TEF,但当 t=0时,计算出的初始测试工作量 W(0)不为 0,这一结论与直觉不相符;③Chatterjee提出的考虑学习函数的 TEF的形式较复杂,且与 Log-logistic TEF的表现相同,即基于这两种 TEF的 SRGM的评估性能一般,因此在相关研究中未得到关注.

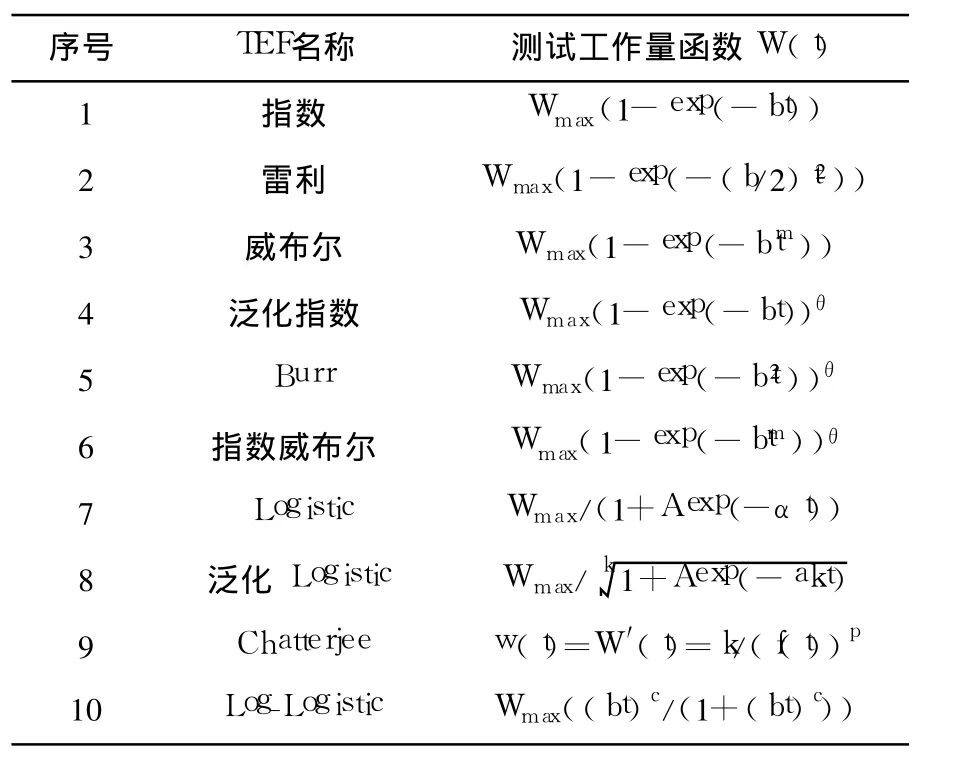
表 1 已有的测试工作量函数

2 考虑 S型 TEF的 SRGM

本节首先提出两种 S型 TEF,在此基础上提出两种考虑 S型 TEF的 NHPP类 SRGM.

2.1 S型TEF

2.1.1 延迟 S型 TEF

利用延迟 S型函数来描述测试工作量随时间的变化趋势,则[0,t]内的累积测试工作量为

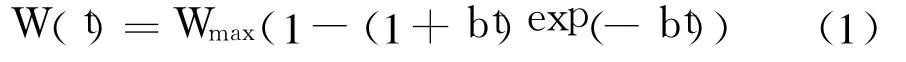
其中 b为测试工作量消耗率,且 b＞0.

由式(1)可知:①W(0)=0,即初始测试工作量为 0;②W(t)为非负值且随时间 t单调递增,这与测试过程中测试工作量的不断增长相符合;③将W(t)对时间 t求导,可得 TEF随时间的变化速率函数为

其中,w(t)是一个先增后减的函数,在 t=1/b时,测试工作量的增长速率达到最大值.

2.1.2 变形 S型 TEF

利用变形 S型函数描述测试工作量随时间的变化形式,则[0,t]内的累积测试工作量为

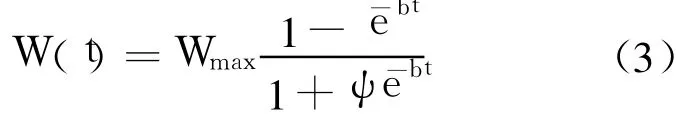
其中 ψ是常量.

由式(3)可知:①W(0)=0;②W(t)为非负值且随时间 t单调递增;③增长速率函数为

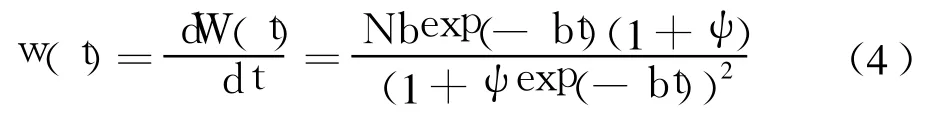
其中,w(t)是先增后减的函数,在 t=lnψ/b时,测试工作量的增长速率达到最大值.

2.2 考虑 S型 TEF的 SRGM(STEF-SRGM)

STEF-SRGM的模型假设如下[6,9,11,14]:

①软件缺陷探测过程服从 NHPP过程,且软件中残存的缺陷总数是一个定值,记为 N;②当前软件失效是由残存缺陷引发的;③在时间间隔[t,t+Δt]内探测到的缺陷数均值与残存缺陷数成正比,该比值表示测试过程中的缺陷探测率;④利用延迟或变形 S型 TEF来描述测试工作量随时间的消耗情况;⑤缺陷一旦被发现,立即被排除且不引入新错.

根据上述假设可得考虑 TEF的指数型 NHPP类 SRGM满足下式[9]:

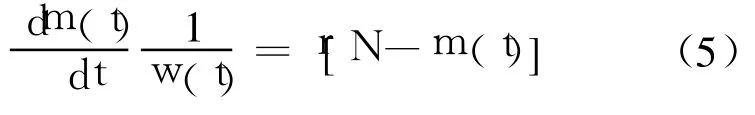
其中,m(t)是[0,t]时间段的探测缺陷数的期望值;r表示每个缺陷被检测到的概率.

在边界条件 m(0)=0下,对式(5)求解可得:

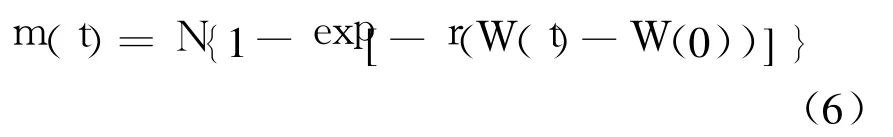
由于 W(0)=0,式(6)可以简化为

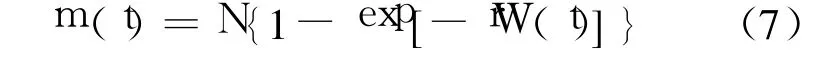
由式(7)可得

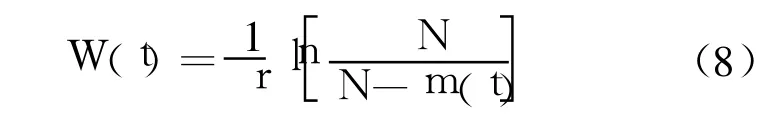
式(7)、式(8)可以定量地反映缺陷探测数均值与所消耗的测试工作量之间的关系.根据式(7),结合式(1)、式(3)即可获得如下两种考虑 S型 TEF的指数型 NHPP类 SRGMs.

2.2.1 考虑延迟 S型 TEF的 SRGM(DSTEFSRGM)

将式(1)代入式(7),可以得到考虑延迟 S型TEF的 NHPP类 SRGM:

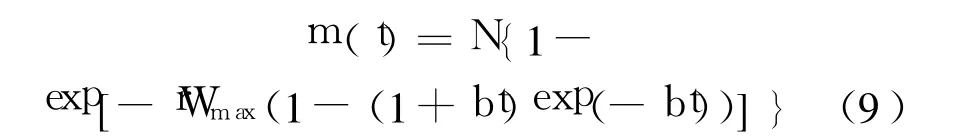
由式(9)可得失效强度函数和最终软件残存的缺陷数:

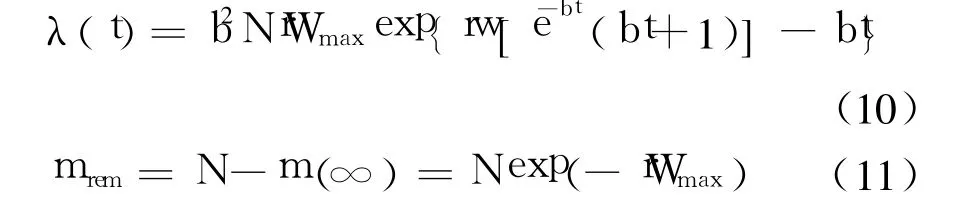
2.2.2 考虑变形 S型 TEF的 SRGM(ISTEFSRGM)

将式(3)代入式(7),得到考虑变形 S型 TEF的NHPP类SRGM:

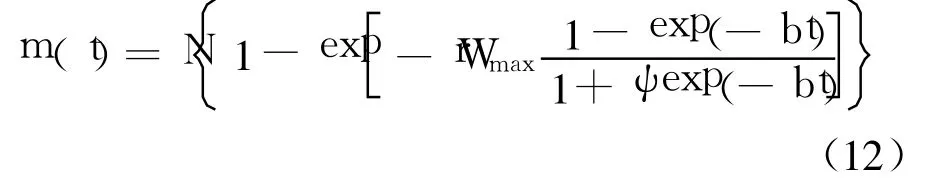
由式(12)可得失效强度函数和最终软件残存的缺陷数:

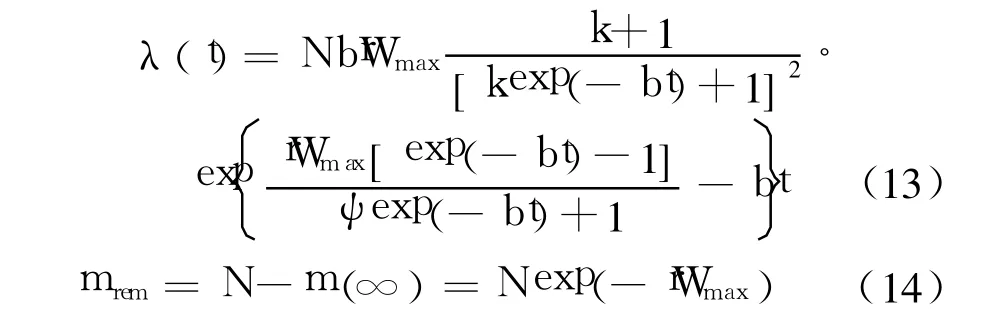
3 实例验证

3.1 实例概述

1)选取 12个 NHPP类 SRGMs作为对比模型,其中前 9个模型为经常用于软件可靠性建模验证研究的经典 NHPP类 SRGMs[1,3],后 3个模型为目前最为典型的 TEF-SRGMs,详见表 2.

2)选择两组真实的失效数据集 Ohba与Wood[6],用于估计模型的参数值并计算模型的拟合结果.这两组数据集均是用于软件可靠性模型性能比较的经典范例,均包含 3类数据,即测试时间(t),测试工作量(W)以及探测缺陷数(m).计算过程中,本文将 Wood数据集中的测试工作量数据缩小 100倍,目的是为了提高模型参数 Wmax的估计质量,且这种缩放处理不会对模型的可靠性评估性能对比产生影响.

3)选用最小二乘估计(LSE,Least Square Estimation)作为模型参数估计方法,LSE产生的估计结果具有无偏性[32].

4)选用 3种经典评价准则作为模型拟合结果的评价准则,分别为均值误差平方和[6](见式(15))、回归曲线方程的相关指数[8](见式(16))、相对误差图[6](RE图,见式(17)).

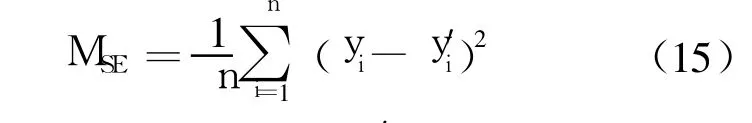
其中,yi为真实的观测数据,y′i为模型计算出的对应 yi的拟合值.MSE值越小,则模型拟合效果越好,也即表明模型的可靠性评估性能越好.

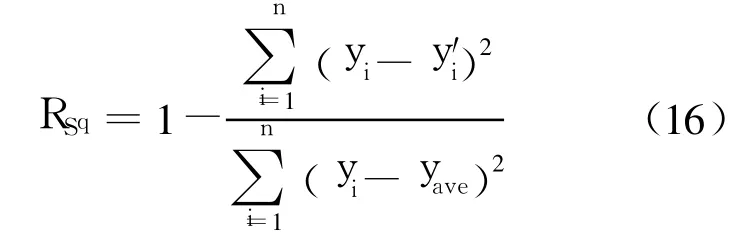
其中,yave表示观测数据 yi的均值.RSq值越接近于1,则模型拟合效果越好.

RE图由模型在每个观测数据点上计算出的RE值(式(17))绘制而成.

RE图整体越接近于 x轴,模型拟合效果越好.

3.2 实例计算结果与分析

表 2分别列出各模型在两组失效数据集上的参数估计值和模型拟合结果,具体分析如下.

表 2 STEF-SRGMs与对比 SRGMs在各组失效数据集上的参数估计与模型拟合结果

1)Ohba数据集上的拟合结果.①在 Ohba数据集上,本文提出的 ISTEF-SRGM的拟合结果为最优(MSE值最小,为 74.05;RSq值最接近于 1,为0.993),且显著好于其它对比模型;但 DSTEFSRGM的拟合效果表现一般.②拟合效果最好的前 5个模型依次为:ISTEF-SRGM、GGO、威布尔-TEF、指数威布尔-TEF、Logistic-TEF.③图 1描述了这 5个拟合效果最优模型对 Ohba数据集中每个探测缺陷数均值的拟合值与实际观测值的对比情形,可看出,ISTEF-SRGM的拟合图形与实际观测值图形的整体增长趋势最为相似,且在许多点上的距离也最为接近.④图 2是根据 5个拟合效果最优模型在 Ohba数据集中每个数据点上的 RE值绘制得到的模型 RE图.可看出,ISTEF-SRGM的 RE图整体上最接近于 x轴,且这 5个模型在多数点上的拟合结果略偏于保守.

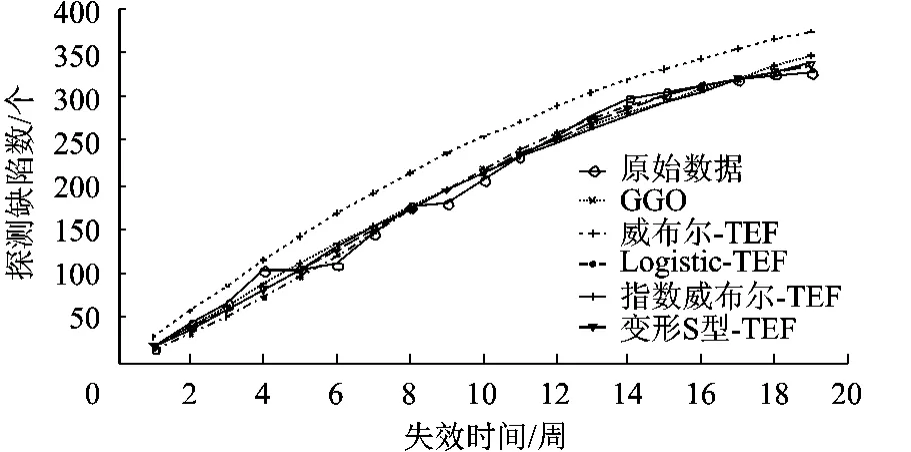
图1 Ohba数据集上的拟合结果

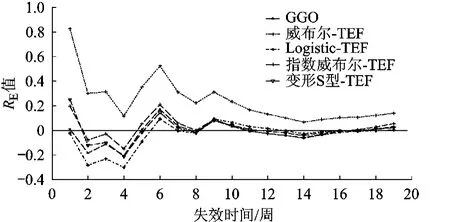
图2 Ohba数据集上的 RE图

2)Wood数据集上的拟合结果.①在 Wood数据集上,本文提出的 ISTEF-SRGM的拟合效果依然为最优(MSE值最小,为 7.88;RSq值最接近于1,为 0.990),且显著好于其它对比模型.但DSTEF-SRGM的拟合效果依然表现一般.②拟合效果最好的前 5个模型依次为:ISTEF-SRGM、IS、GGO、GO和 OID.③图 3描述了这 5个拟合效果最优模型对 Wood数据集中每个探测缺陷数均值的拟合值与实际观测值的对比情形.可看出,ISTEF-SRGM的拟合图形与实际观测值图形的整体增长趋势最为相似且在许多点上的距离也最为接近.④图 4是根据 5个拟合效果最优模型在Wood数据集中每个数据点上的 RE值绘制得到的模型 RE图.可看出,ISTEF-SRGM在 Wood数据集上的 RE图整体上最接近于 x轴,且这 5个模型在多数点上的拟合结果略偏于乐观.

图3 Wood数据集上的拟合结果

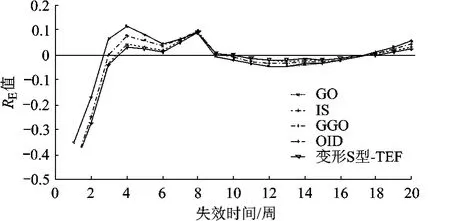
图4 Wood数据集上的 RE图

3)实例计算结果分析.综上,可得出如下结论:①本文提出的考虑变形 S型 TEF的 SRGM在两组数据集上的拟合效果均是最优的,显著优于绝大部分对比模型,从而证明 ISTEF-SRGM在模型评估性能上具有很好的有效性及适用性;②对于 Ohba数据集,拟合效果最优的 5个模型中有 4个是 TEF-SRGM,所以在软件可靠性建模中考虑TEF,确实可以有效地改进传统模型的评估性能;③ISTEF-SRGM的评估性能显著优于 2种最典型的 TEF-SRGM,即 Logistic-TEF和指数威布尔 TEF模型,从而表明了本文研究成果具有显著的理论研究意义;④本文提出的考虑延迟 S型 TEF的SRGM(DSTEF-SRGM)在两组数据集上的拟合效果均表现一般.分析原因,可能是因为延迟 S型TEF并不适合用于描述测试工作量随时间的增长趋势、进而影响了模型的评估性能.因此,选择合适的 TEF对于保证 TEF-SRGM的可靠性评估性能具有重要意义.

4 结束语

本文提出两种 S型 TEF,即延迟 S型与变形S型 TEF,在此基础上提出两种考虑 S型 TEF的SRGMs,并在两组经典失效数据集上,将这 2种STEF-SRGMs与若干经典 SRGMs及典型的 TEF-SRGMs进行了对比研究.结果表明,本文提出的考虑变形 S型 TEF的 SRGM的可靠性评估性能及模型适用性显著有效,具有良好的理论研究意义与工程应用前景.

在未来的研究工作中,将关注以下问题:①将变形 S型TEF与S型 NHPP类软件可靠性模型相结合;②在建模过程中考虑不完美排错的情况;③与基于测试工作量函数的 S型 NHPP类软件可靠性模型进行对比研究.

References)

[1]Lyu M R.Handbook of software reliability engineering[M].New York:McGraw Hill,1996

[2]Gokhale S S,Lyu M R.A simulation approach to structure-based software reliability analysis[J].IEEE Trans on Software Engineering,2005,31(8):643-656

[3]Pham H.Software reliability[M].Singapore:Springer-Verlag,2000

[4]Gana A,Huang S T.Statistical modeling applied to managing global 5ess-2000 switch software development[J].Bell Labs Technical Journal,1997,2(1):144-153

[5]Kruger G A.Validation and further application of software reliability growth models[J].Hewlett-Packard Journal,1989,40(4):75-79

[6]Huang C Y,Kuo SY,Michael R L.An assessment of testing-effort dependent software reliability growth models[J].IEEE Transactions on Reliability,2007,56(2):198-211

[7]Shibata K,Rinsaka K,Dohi T.Metrics-based software reliabil-ity models using non-homogeneous Poisson processes[C]//Proc of the 17thIEEE International Symposium on Software Reliability Engineering.Washington DC:IEEE Computer Society,2006:52-61

[8]谢景燕,安金霞,朱纪洪.考虑不完美排错情况的 NHPP类软件可靠性增长模型[J].软件学报,2010,21(5):942-949 Xie JY,An JX,Zhu JH.NHPP software reliability growth model considering imperfect debugging[J].Journal of Software,2010,21(5):942-949(in Chinese)

[9]Kuo SY,Huang CY,Michael R L.Framework for modeling software reliability,using various testing-efforts and fault-detection rates[J].IEEE Transactions on Reliability,2001,50(3):310-320

[10]Norman E F,Martin N.A critique of software defect prediction models[J].IEEE Transactions on Software Engineering.1999,25(5):675-689

[11]Huang CY.Analysis of incorporating logistic testing-effort function into software reliability modeling[J].IEEE Transactions on Reliability,2002,51(3):261-270

[12]Musa JD,Iannino A.Software reliability,measurement,prediction and application[M].New York:McGraw Hill,1987

[13]Yamada S,Hishitani J,OsakiS.Software reliability growth model with Weibull testing effort:a model and application[J].IEEE Transactions on Reliability,1993,42(1):100-106

[14]Ahmad N,BokhariM U,Quadri SM K,et al.The exponentiated Weibull software reliability growth model with various testing efforts and optimal release policy[J].International Journal of Quality＆Reliability Management,2008,25(2):211-235

[15]Quadri SM K.Non homogeneous Poisson process software reliability growth model with generalized exponential testing effort function[J].RAU Journal of Research,2006,16(2):159-163

[16]Ahmad N,Khan M G M,Quadri SM K,et al.Modeling and analysis of software reliability with Burr type X testing-effort and release-time determination[J].Journal of Modeling in Management,2009,4(1):28-54

[17]Huang C Y.Cost-reliability-optimal release policy for software reliability models incorporating improvements in testing efficiency[J].The Journal of Systems and Software,2005,77:139-155

[18]Huang C Y.Optimal release time for software systems considering cost,testing-effort,and test efficiency[J].IEEE Transactions on Reliability,2005,54(4):583-591

[19]Bokhari M U,Ahmad N.Analysis of a software reliability growth models:the case of log-logistic test-effort function[C]//Proceedings of the 17thInternational Conference on Modeling and Simulation.Montreal,Canada:Acta Press,2006:540-545

[20]Chatterjee S,Misra R B,Alam SS.Joint effectof test effort and learning factor on software reliability and optimal release policy[J].International Journal of System Science,1997,28(4):391-396

[21]Ahmad N,Khan M G M.A study of testing-effort dependent inflection S-shaped software reliability growth models with imperfect debugging[J].International Journal of Quality＆Reliability Management,2010,27(1):89-110

[22]Jha PC,Gupta D,Yang B,et al.Optimal testing resource allocation during module testing considering cost,testing effort and reliability[J].Computers＆Industrial Engineering,2009,57:1122-1130

[23]Lin C T,Huang C Y.Enhancing and measuring the predictive capabilities of testing-effort dependent software reliability models[J].The Journal of Systems and Software,2008,81:1025-1038

[24]Huang C Y.Performance analysis of software reliability growth models with testing-effort and change-point[J].The Journal of Systems and Software,2005,76:181-194

[25]Kapur P K,Gupta A.Testing effort control using flexible software reliability growth modelwith change point[J].International Journal of Performability Engineering,2006,2(3):245-262

[26]Lin C T,Huang C Y,Chang J R.Integrating generalized Weibull-type testing-effort function andmultiple change-points into software reliability growth models[C]//12th Asia-Pacific Software Engineering Conference.Los A lam itos:IEEE Computer Society,2005:431-438

[27]Kapur P K,Goswami DN,Amit B,et al.Flexible software reliability growth model with testing effort dependent learning process[J].Applied Mathematical Modeling,2008,32:1298-1307

[28]Kapur P K,Grover P S.Modelling an imperfect debugging phenomenon with testing effort[C]//Proceedings of the 4thSoftware Reliability Engineering.Los Alamitos:IEEE,1994:178-183

[29]Kapur P K,Omar S,Anu G A,et al.Unified framework for developing testing effort dependent software reliability growth models[J].WSEAS Transactions on Systems,2009,4(8):521-531

[30]Yamada S,Ohba M,Osaki S.S-shaped software reliability growth modelsand their applications[J].IEEE Transon Reliability,1984,R-33(4):289-292

[31]Ohba M.Inflection S-shaped software reliability growth models[M].Stochastic Models in Reliability Theory.Berlin:Springer,1984:144-162

[32]Su Y S,Huang C Y.Neural-network-based approaches for software reliability estimation using dynam ic weighted combinational models[J].The Journal of Systems and Software,2007,80:606-615

[33]Yamada S,Tokuno K,Osaki S.Imperfect de bugging models with fault introduction rate for software reliability assessment[J].International Journal of Systems Science,1992,23(12):2241-2252

(编 辑 :娄 嘉)

Software reliability growth model with S-shaped testing effort function

Li Qiuying Li Haifeng Lu Minyan Wang Xuecheng

(School of Reliability and Systems Engineering,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)

The shape of the observed reliability grow th curve depends strongly on the time distribution of the testing effort.Thus,the reliability estimation power of software reliability growth model(SRGM)can be improved by considering the testing effort function(TEF).Due to the integrated effects of software structure and learning factor on testing process,testing effort increasing rate may exhibit an S-shaped varying trend first increasing and then decreasing.To accurately describe this S-shaped varying trend,two S-shaped testing effort functions were proposed first,i.e.delayed S-shaped TEF and inflected S-shaped TEF,which were simple and flexible.Then two new SRGMs were put forward by combining two S-shaped TEFs into SRGM,i.e.DSTEFSRGM and ISTEF-SRGM.Finally,for two real failure data-sets,the case study was done by comparing these two S-shaped TEF-SRGMs with several classical SRGMs and other representative SRGMs considering TEF in the form of estimation power.The result shows that compared with these comparison models,the proposed ISTEF-SRGM has the best fitting results on each data-set.In other words,the proposed ISTEF-SRGM provides novel applicability and a significantly better power of reliability estimation.

software reliability;testing;reliability analysis;growth;models

TP 311

A

1001-5965(2011)02-0149-06

2010-07-13

李秋英(1973-),女,黑龙江大庆人,讲师,li qiuying@buaa.edu.cn.