压电智能板振动主动控制有限元模拟

钱 锋， 王建国， 曲 磊

(合肥工业大学土木与水利工程学院，安徽合肥 230009)

利用压电效应，贴于结构表面或埋于结构内部的压电材料既可作为传感器又可作为致动器[1，2]，因此压电材料是弹性结构主动控制中广泛使用的智能材料，文献[3]最早利用压电材料的这些特性研究了梁的振动控制。压电智能结构的分析需要解决电-力耦合等复杂力学问题，尤其是对于板类或大型复杂结构，采用解析的方法是相当困难的，且受到许多假设条件的限制。文献[4]提出了考虑压电层合结构刚度、质量和力电耦合效应的梁、板和壳单元，并利用常增益负速度反馈、Lyapunov反馈和线性二次型(LQR)方法实现了板壳结构在冲击、简谐和任意激励作用下的模态控制。文献[5]以有限元模态分析为基础，实现了压电智能梁板结构在状态空间形式下的振动控制。文献[6]利用ANSYS软件对圆柱壳结构进行模态分析和质量归一化，得到结构的模态矩阵，进而实现了结构振动的LQG控制。文献[7]基于ANSYS参数化语言，研究了压电智能悬臂梁的PID控制。

在给定控制策略下，智能结构振动控制效果主要与致动器/传感器的数量和位置分布有关。薄板是许多工程应用中较常见的结构，通常仅用1～2个压电片便可达到对板类结构较低阶模态振动控制的目的，但对于大型复杂结构，仅用单一的压电致动器来控制结构的振动是很困难的，同样仅利用1个传感器来获得结构的振动信息也是不够准确的。在整个结构或结构的绝大部分表面上粘贴压电致动器/传感器能够起到很好的控制和感知效果，但制作比较困难，代价也比较昂贵，更主要的是很大程度上改变了系统的特性和动力响应。为克服这些缺陷和困难，文献[8]提出了利用多个离散的分布式压电致动器/传感器来控制板结构的多模态振动。

本文在线弹性压电层合结构有限元动力方程[2]的基础上，进一步推导了压电智能结构的主动控制方程，采用ANSYS自带三维八节点实体耦合单元模拟压电致动器/传感器，分别用So lid45实体单元和Shell63壳单元模拟主结构，运用ANSYS参数化语言(APDL)建立压电智能板结构的有限元模型进行模态分析，将所得四边固支方形板主结构振动频率与现有文献中解析解和有限元解进行了对比，验证了本文模型的正确性。进而将压电智能结构系统电-力耦合有限元动力方程转化为模态坐标下的系统状态空间方程，采用LQR全状态最优反馈控制，以控制多阶模态的振动为目标，考虑压电致动器/传感器的分布对主结构模态应变分布的影响，本文研究了上下表面对称粘贴9对压电片的四边固支智能板结构的多模态振动控制，并对其进行了有限元数值模拟。

配置9对压电片的智能板结构如图1所示。

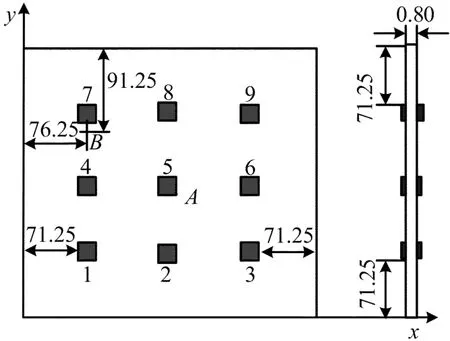
图1 配置9对压电片的智能板结构

1 线弹性压电层合结构控制方程

线弹性压电层合结构有限元动力方程为:

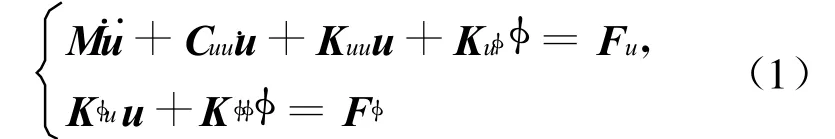
其中，u、φ为节点位移和电势;M、Kuu为结构整体质量矩阵和刚度矩阵;K uφ、Kφu为压电耦合刚度矩阵;Kφφ为介电刚度矩阵;C uu为阻尼矩阵;F u、Fφ为作用在结构上的荷载列阵和电荷列阵。在实际应用中，通常考虑结构的阻尼为结构的质量矩阵和刚度矩阵的线性组合，即

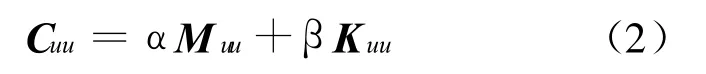
其中，α和β为结构瑞利阻尼系数。电荷与电压之间的关系式可表示为:

其中，c p为压电材料的电容;V为节点电压列阵。

将方程(1)第2式与(3)式代入方程(1)的第1式，考虑结构阻尼，得干扰荷载和输入控制电压作用下仅用节点位移表示的压电层合结构有限元动力方程:

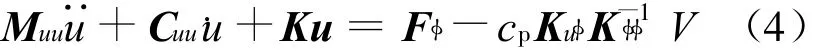
其中，K=K uu-K uφK-1φφKφu。

设系统关于质量归一化的特征向量矩阵为Φ，模态坐标为η，将系统动力方程(4)转化为模态空间坐标下的解耦方程，即

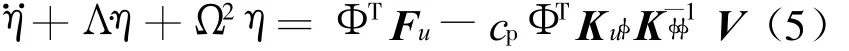
其中，Λ=diag[2ξ1ω1，2ξ2ω2，…];Ω2=diag[，，…];ξi=(α+)/2ωi。

ωi为结构第i阶频率，ξi为i阶模态阻尼比。将方程(5)转化为状态空间方程，即:

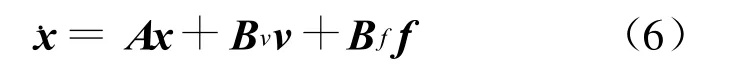
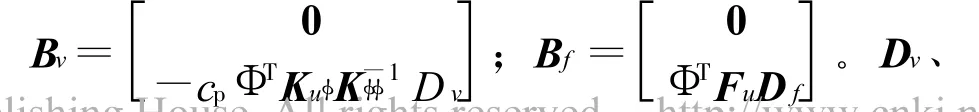
D f分别为控制电压和干扰力作用位置矩阵。

系统的输出方程为:

输出矩阵C与特征向量矩阵Φ有关。

2 LQR全状态反馈最优控制

采用全状态反馈控制电压可写为:

其中，K为使得(9)式取极小值的控制反馈增益矩阵。(9)式为性能指标函数，即

其中，Q和R为对称正定权矩阵。通常将系统能量作为性能指标函数，因此设

其中，αi为第i阶状态变量权值，可根据各阶模态对系统的贡献大小来确定;γ为控制电压权值。

将反馈控制电压(8)式代入(9)式得:

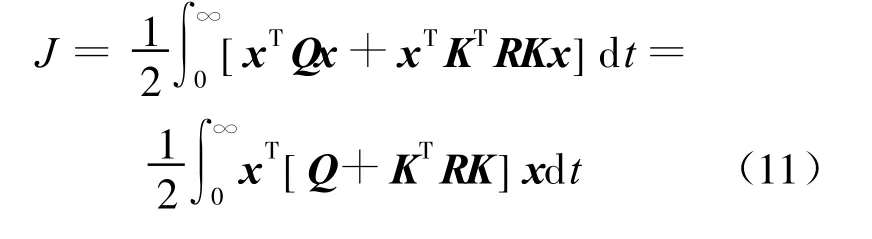
因此增益矩阵为:

Research on the DC Control and Protection Configuration of VSC-HVDC Technology for Offshore Platform BAI Jinchuan,ZHANG Xuguang(109)

Riccati方程为:

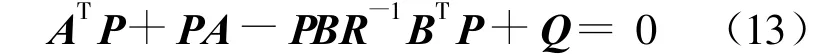
P可由(13)式求得。

3 数值算例

本文利用通用有限元软件ANSYS建立了图1所示的配置9对压电致动器/传感器智能板的有限元模型。主结构板是金属铝材料，主结构及压电材料属性参数如下。

主结构梁几何参数:305 mm×305 mm× 0.8 mm。

致动器/传感器:10 mm×10 mm×1 mm。材料参数和压电材料参数见文献[5]。

3.1 模态分析

在进行动力分析及仿真之前，为验证本文有限元模型的正确性，首先分别用三维八节点实体单元(Solid45)和平面四节点壳单元(Shell63)对四边固支主结构方形板进行模态分析，主结构前7阶自振频率与有限元方法解[8]和解析解[9]的对比见表1所列。

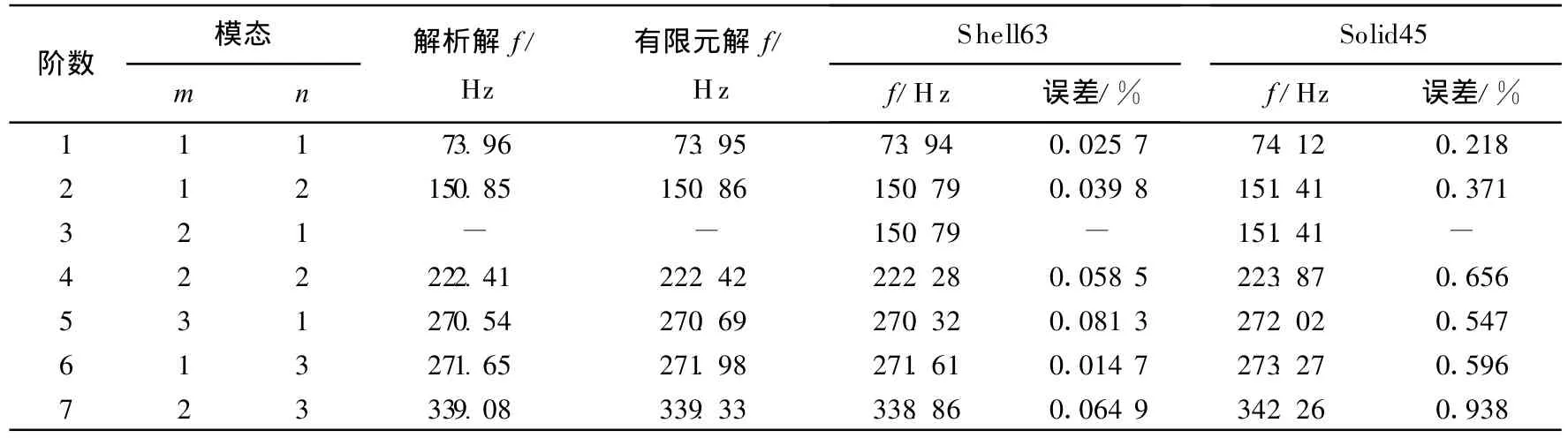
表1 四边固支主结构板自振频率

通过比较可知，采用ANSYS自带实体单元和平面单元均可准确地分析本文模型，但由于板属于二维问题，采用平面壳单元分析与精确解更为吻合，本文仿真分析中均用Shell63单元模拟主结构，四边固支板主结构的前6阶振型如图2所示。本文采用图1所示的配置9对10 mm× 10 mm的致动器/传感器的智能结构系统，主结构采用Shell63单元模拟，压电致动器/传感器采用Solid5单元模拟，指定单元长度为板边长的1/ 60划分单元，其中Shell63单元4 096个，Solid5单元72个。配置9对致动器/传感器时系统前6阶振型如图3所示。

图2 主结构板前6阶模态

图3 配置9对压电片的智能板前6阶模态

对比图2和图3可知，离散分布式致动器/传感器对系统模态影响比较明显，但对主结构特征模态应变/曲率分布的影响较小。综合以上模态分析结果可知，利用较少数目的致动器/传感器来控制结构多模态振动是可行的。

3.2 主动振动控制分析及仿真

3.3 智能板各阶模态振动控制仿真

为研究离散分布式压电致动器/传感器对系统各阶模态振动的控制情况，对图1所示配置的9对压电片分3种情况:Case1，板中心位置第5个压电致动器单独作用;Case2，除第5个之外板四周的8个压电致动器同时作用;Case3，9个致动器同时作用。Case1情况下瞬时荷载作用在板中心A点时，A、B点振动控制时域响应和频域响应分别如图4、图5所示。

由图4、图5可知，第5个致动器对结构各阶模态振动控制效果明显，且当系统响应权系数αi不变时，控制输入权系数γ越小控制效果越好;当γ不变时，αi越大控制效果越好。由于方形板关于中心点A对称，因此瞬时荷载作用在点A时仅引起了对称模态的振动，这说明第5个致动器位于板的中心位置可以有效地抑制板对称模态的振动。

图4 荷载作用于A点Casel时A、B点控制时域响应

图5 荷载作用于A点Casel时A、B点控制前后频域响应

控制电压权值γ=1E11、Case2和Case3情况下，瞬时荷载作用在板中心A点时，A、B点振动前后频域响应如图6所示。由图6可知，Case2时系统的第1阶模态振动也得到了较理想的控制作用，与文献[6]中系统1阶模态振动并没有得到明显的控制相比，本文所提出的致动器/传感器配置方法更合理。Case3情况下由于9个致动器同时作用，因此系统各阶模态的振动均可得到明显控制。

图6 荷载作用于A点Case2，Case3时A、B点频域响应

Case1情况下瞬时荷载作用在B点时，A、B点振动前后时域响应和频域响应分别如图7、图8所示。

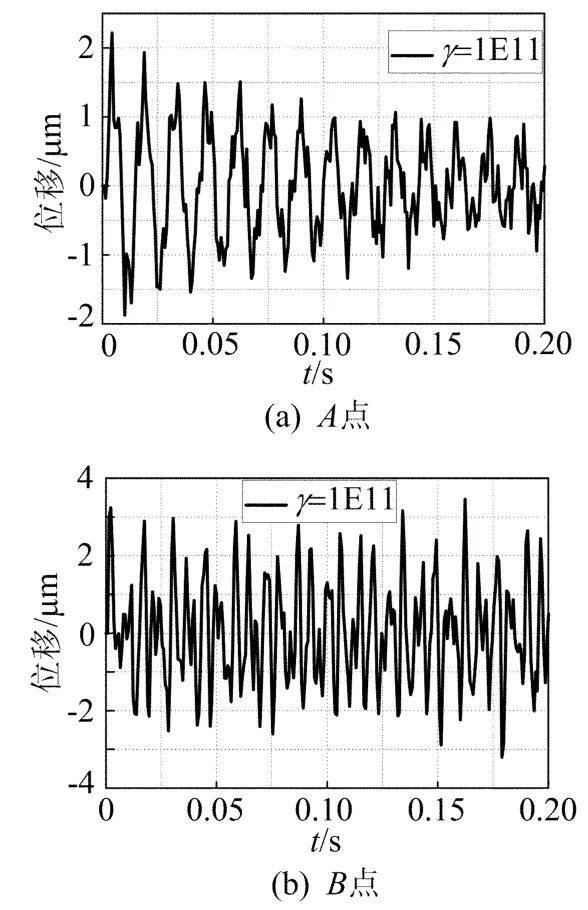
图7 荷载作用于B点Case1时A、B点控制时域响应

由图7、图8可看出，第5个压电致动器对结构各阶模态振动控制效果明显;由于第5个致动器位于板中心处，其对系统振动起到抑制作用的同时，也在A点激发了其它模态的振动。从图8b可以看出第5个致动器对于B点的振动控制作用很小，这是由于第5个致动器位于板中心位置仅对第1、2、4、6、7、8、10、12阶模态起到了控制作用，而对3、5、9、11阶模态的振动基本没有控制作用。

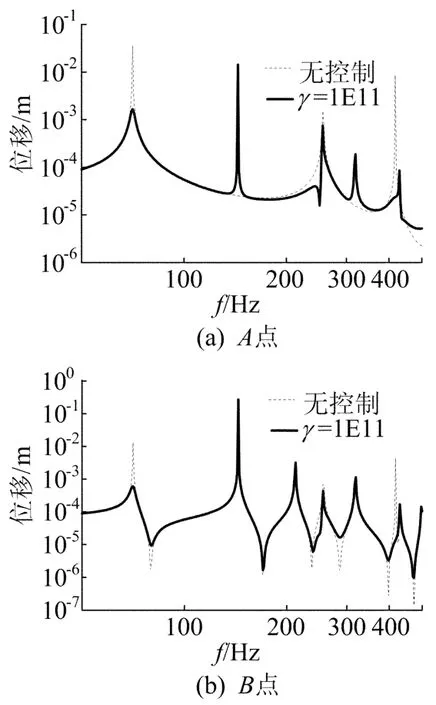
图8 荷载作用于B点Case1时A、B点控制前后频域响应

控制电压权值γ=1E11，Case2和Case3情况下，瞬时荷载作用在B点时，A、B点振动前后频域响应如图9所示。由图9a可知，2种情况对于B点激励在A点的响应均有明显的控制效果。

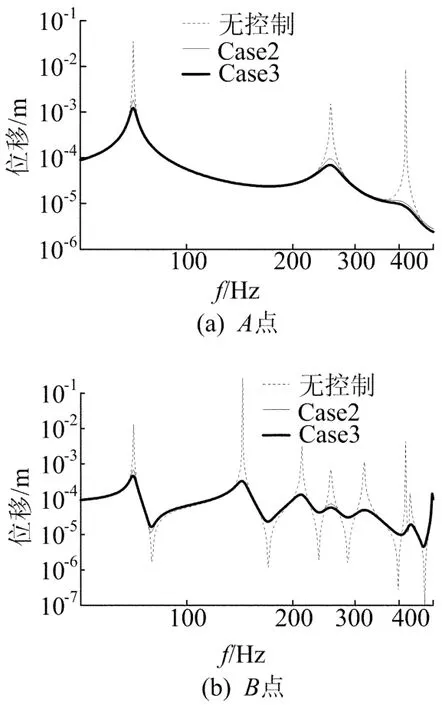
图9 荷载作用于B点Case2、Case3时A、B点频域响应

由图9b可知，Case2和Case3情况下对各阶模态的振动均可起到有效的控制。因此，配置9对压电致动器/传感器，能够在几乎不改变主结构特征模态应变分布的情况下，通过选择适当的控制电压权值使结构各阶模态的振动得到理想的控制效果，同时也可以通过调整状态变量权值αi来加强对相应模态的控制。

4 结束语

本文由线弹性压电层合结构有限元动力方程，进一步推导了压电智能结构的主动控制方程。运用ANSYS参数化语言(APDL)建立了四边固支方形压电智能板结构的有限元模型，并进行模态分析，将系统耦合有限元动力方程转化到模态坐标下的状态空间方程。采用LQR全状态最优反馈控制，考虑离散分布式压电致动器/传感器对于主结构特征模态应变/曲率分布的影响，分析了离散分布压电致动器对系统各阶模态的控制效果，结果表明:离散的分布式压电致动器/传感器可有效控制板结构的多模态振动;离散分布式压电致动器/传感器对于主结构特征模态应变/曲率分布的影响较小，合理选择压电致动器/传感器的数量及分布与寻求最优控制率一样重要;压电致动器在对系统产生控制作用的同时，由于受其分布位置的影响可能会引起或加强系统其它模态的振动。将本文数值算例结果与现有文献结果进行对比发现，配置9对压电致动器/传感器可以使结构各阶模态的振动得到理想的控制效果。tures using piezoelement[D].Otlaw a:Conletom University，1997.

[2] Zabihollah A，Sedagahti R，Ganesan R.Active vibration suppression of smart lam inated beam susing layerw ise theory and an op timal control strategy[J].Smart M ater Stru ct，2007，16:2190-2201.

[3] Bailey T，Hubbard JE.Distributed piezoelectric-polymer active vibration control of a cantilever beam[J].Jou rnal of Guidance Control，1985，8(5):605-611.

[4] Narayanan S，Balamurugan V.Finite element modelling of piezolam inated smart structures for active vibration con trol w ith distribu ted sensorsand actuators[J].Journalof Sound and V ibration，2003，262:529-562.

[5] Xu S X，Koko T S.Finite element analy sisand design of actively controlled piezoelectric smart structu res[J].Finite E lements in Analysis and Design，2004，40:241-262.

[6] Sohn JW，Kim H S，Choi S B.Active vib ration control of smart hull structures using piezoelectric actuators[J].Proc IMech E Part C:J M echanical Engineering Science，2006，220:1329-1337.

[7] 钱 锋，王建国.压电智能结构振动控制的数值模拟[J].合肥工业大学学报:自然科学版，2010，33(1):76-80.

[8] Lim Y H.Finite-elemen t sim ulation of closed loop vibration controlof a smart plate under transient loading[J].Smart M ater Stru ct，2003，12:272-286.

[9] Leissa A W.V ib ration of plates[M].Washington D C: NASA SP-160，1969.

[10] 欧进萍.结构振动主动控制:主动、半主动和智能控制[M].北京:科学出版社，2003:82.