基于满意度的贮备多阶段任务系统可靠性优化

俞 建 胡 涛 杨春辉

(海军工程大学管理工程系，武汉 430033)

基于满意度的贮备多阶段任务系统可靠性优化

俞 建 胡 涛 杨春辉

(海军工程大学管理工程系，武汉 430033)

分析了多阶段任务系统成功运行的条件;在冷贮备系统的可靠性计算模型的基础上提出了单元是二态，失效率服从指数分布的冷贮备多阶段任务系统的可靠性计算模型;建立了系统可靠度、体积、重量和价格的子满意度函数，并利用层次分析法确定各个子满意度函数的影响因子;构建了基于综合满意度函数的贮备多阶段任务系统可靠性冗余优化模型，应用微粒群算法对模型进行求解.算例通过一个3个阶段的冷贮备系统来阐述该方法的应用，并验证了模型的合理性及算法的有效性.

冗余;优化;可靠性分析;微粒群算法

多阶段任务系统(PMS，Phased Mission Systems)是指系统在连续完成多个阶段任务过程中，任务成功与部件的关系不断变化的系统.它自文献［1］提出以来，引起了学术界的一定关注.近30多年来，多阶段任务系统的研究得到了重要的发展.一些研究者关注于解决多阶段任务系统的阶段独立性问题，主要采用基于状态空间的分析方法，包括 Markov 方法［2－3］和 Petri网方法［4－6］.基于状态空间的分析模型能够完整、准确地表述PMS的动态行为和系统部件在PMS运行过程中的各种依赖关系，该方法表达能力强，方法灵活，但存在状态空间爆炸的问题.为解决此问题，文献［7－8］提出了采用组合模型，因为它在二元决策图(BDD，Binary Decision Diagrams)操作处理时采用了低计算复杂度和低存贮空间消耗.

近年来，研究人员将不完全覆盖［9］(IPC，Imperfect fault Coverage)、共因失效［10］(CCF，Common Cause Failure)和多模式失效［11］(MMF，Multi-Mode Failure)引入了PMS问题中.本文所研究的是贮备多阶段任务系统的冗余优化问题.随着科学技术的发展，武器装备越来越复杂，执行的任务也越来越多样化.而为保证任务的完成，许多设备都采用了贮备系统来提高它的可靠性.所以开展贮备多阶段任务系统的冗余优化研究有利于合理的配置资源，节约成本，提高效率.

1 贮备多阶段任务系统可靠度计算

1.1 贮备多阶段任务系统

为了提高系统可靠性，除了安装必备的工作单元外，还可以贮备一些单元，以便当工作单元失效时，贮备单元接替工作，直到所有贮备单元失效后，工作单元再失效时，系统才失效.贮备系统又分为冷贮备、温贮备.所谓冷贮备是指贮备单元在贮备期间不失效也不劣化，贮备时间的长短对以后使用时的工作寿命没有影响.温贮备系统单元在贮备期间内可能失效，其存贮失效率一般低于工作失效率.

贮备多阶段任务系统是指在完成一连串的任务过程中，在不同的任务阶段，贮备系统具有不同的内部结构、系统状态、任务成功准则和系统内部行为.

1.2 系统可靠度的计算

1)冷贮备系统.假若一个冷贮备系统由一个工作单元、n个贮备单元和一个转换开关组成.转换开关完全可靠.又设这n+1个单元相互独立且都服从失效率为λ的指数分布.根据文献［12］可知，在泊松分布的物理意义下，一个系统在(0，t)时间区间内，发生k个单元失效的概率为

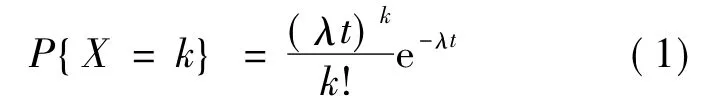
由于n个单元失效，而系统仍不失效，故此冷贮备系统的可靠度为

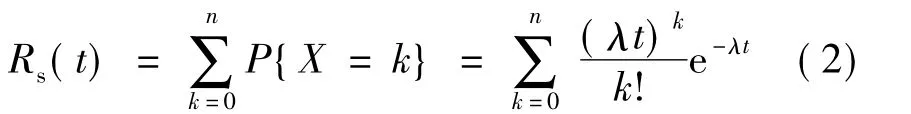
对于系统由n+m个同型单元组成，其中有m个单元串联工作，其余n个单元作冷贮备.当m个工作单元中有一个失效时(假设同一时刻，两个或两个以上单元同时失效的概率为0)，则贮备单元之一立即完成瞬间替换，直到贮备单元全部替换完毕后，工作单元再失效，系统才失效.为了求系统的可靠度，可将m个串联工作单元看成是一个失效率为mλ的等效单元，这样整个系统就等效成一个失效率为mλ的工作单元和n个失效率为mλ的冷贮备单元的系统.那么此冷贮备系统的可靠度为

2)冷贮备多阶段任务系统.为方便说明，首先假设ti表示阶段i的时间;表示第i个阶段中，单元j的失效率;表示第i个阶段中，单元j串联工作的个数;表示第i个阶段中，单元j作冷贮备的个数表示第i个阶段中，单元j失效的个数.对于的计算是根据初始阶段单元j总个数减去第i个阶段前的i－1个阶段内单元j失效的总个数再减去第i个阶段内单元j串联工作的个数Mji，即

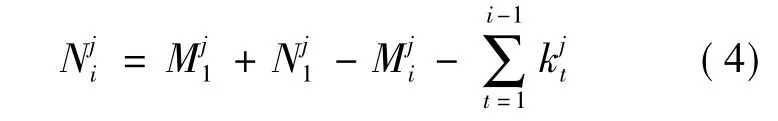
假设一个冷贮备多阶段任务系统由N个子系统串联组成.每个子系统又由若干个同型单元串联工作和一些冷贮备件，各单元之间相互独立且服从指数分布.图1为此系统在阶段i时的可靠性框图.

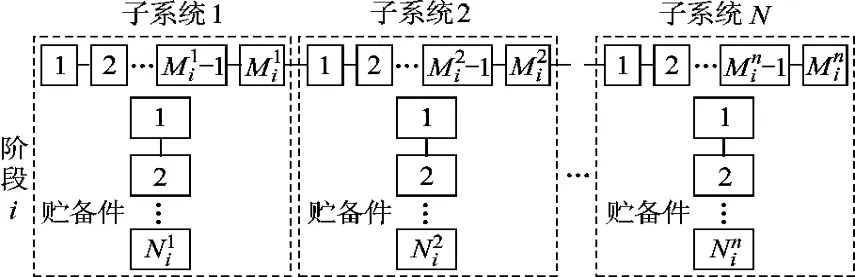
图1 贮备多阶段任务系统第i阶段的可靠性框图

根据式(3)可得此贮备多阶段任务系统在阶段i内的可靠度为

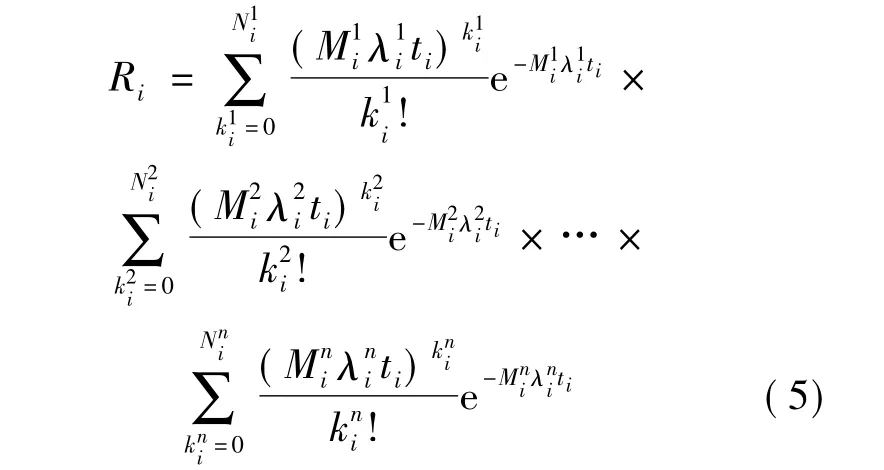
对于n个阶段来说，N个子系统之间是相互独立的，所以可单独对其中一个子系统J在n个阶段内的可靠性进行分析.子系统J在阶段1由个单元j串联工作和个单元j作冷贮备.而第2阶段的单元数为第1阶段单元总数扣除在第1阶段内失效的单元个数，其中一部分作为工作单元另一部分就是贮备单元.同理一直到第n个阶段.当出现时，则表示系统在此阶段的工作单元数不能满足工作需要，即此阶段工作失效，从而导致整个贮备多阶段任务系统的可靠度为0.所以子系统J在n个阶段的可靠度:

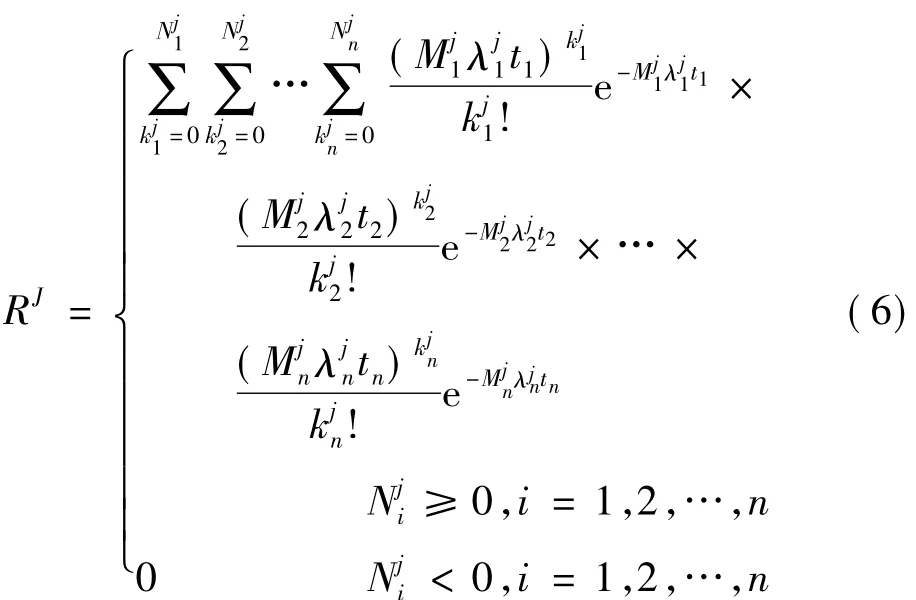
同理可以得所有N个子系统在n个阶段的可靠度R1，R2，…，RN.因为在整个贮备多阶段任务系统中N个子系统是串联的，所以此贮备多阶段任务系统的可靠度为

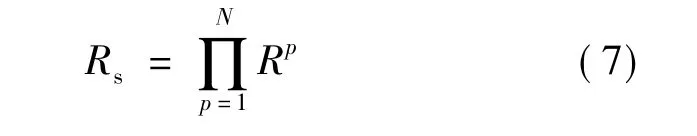
2 基于满意度函数优化模型的构建

对于贮备多阶段任务系统可靠性冗余优化问题，它涉及到系统的可靠度约束、体积约束、重量约束和价格约束4个方面的影响因素.要构建冗余优化总体满意度函数首先要确定这4个子项的满意度函数.

1)系统可靠度满意度函数.系统可靠度Rs是整个系统能否达到设计要求的重要指标，它必须大于等于系统预期的设计可靠度R0且可靠度越高越满意.因此，系统可靠度满意度函数R'可定义为

2)体积满意度函数.在对系统进行设计时，当系统实际体积V在设计体积V0范围内时为满意，满意度为1.但为了保证满足其它重要指标的前提下(如系统可靠度)，系统实际体积可以超出一些，这里对体积给出了一定的松弛余量 σV(σV=0.3)，但超出设计体积所付出的代价是呈指数增长的，所以满意度会呈指数下降(本文取2次方).若实际体积再大，超过了最大承受量(V0+σVV0)，则不满意，满意度为0.所以体积满意度函数V'定义为

3)重量满意度函数.其设计思想与体积满意度函数类似，重量满意度函数m'可定义为

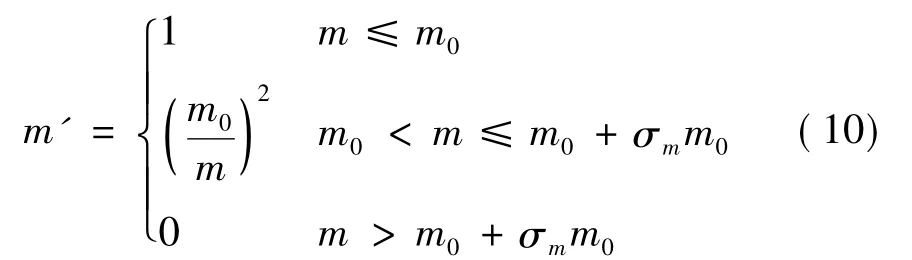
4)价格满意度函数.当实际价格小于等于设计价格时为满意，满意度为1.当实际价格大于设计价格时，满意度下降.所以价格满意度函数C'可设计为

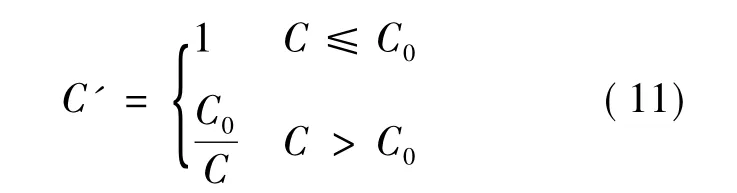
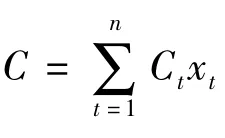
综合上述 R'，V'，m'和 C'构建总体满意度函数F.冗余优化总体满意度函数定义为

式中，ω1，ω2，ω3，ω4分别为 R'，V'，m'，C'在总体满意度函数F中的权系数，有ω1+ω2+ω3+ω4=1.对权系数 ω1，ω2，ω3，ω4的值，可以采用层次分析法进行确定.

3 模型的求解算法及步骤

以上所建模型显然是非线性的，一般采用智能算法予以求解.本文采用微粒群优化算法(PSO，Particle Swarm Optimization)，该方法具有良好的变量适应性和全局最优化能力的特点［13－14］，基本步骤如下:

1)初始化.设置微粒群的规模M，惯性权值ω，加速常数c1，c2，最大允许迭代次数r，各微粒的初始速vi和位置xi，并将各微粒的Pi设置为初始位置，取Pi中的最优值为Pg.

2)按目标函数评价各微粒的适应值，即分别对每个微粒计算目标函数值.

3)对每个微粒，比较其当前适应值和其个体历史最好适应值Pi，若当前适应值更优，令当前适应值为其个体历史最好适应值，并保存其为个体历史最好位置.

4)比较群体所有微粒的当前适应值Pi和全局历史最好适应值Pg，若某微粒的当前适应值更优，则令该微粒的当前适应值Pi为全局历史最好适应值Pg，并保存该微粒的当前位置为全局历史最优位置.

5)根据微粒群速度和位置更新方程(见式(13))来调整微粒群的速度和位置.

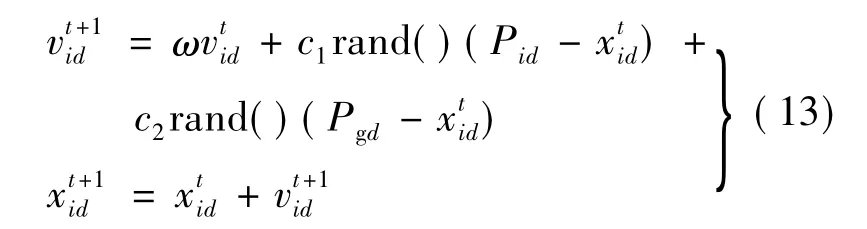
式中，d表示第 d 个微粒，d=1，2，…，M.

6)若满足停止条件(迭代次数超过最大允许迭代次数)，搜索停止，输出结果;否则返回步骤2)继续搜索.

4 算例

某型试验舰船上的电源系统，它由A，B两个子系统组成.两子系统分别由单元a和单元b组成的冷贮备系统.预计某次试验要经历3个阶段.阶段参数见表1，系统和部件参数见表2.要使在这次试验中，此电源系统的可靠度达0.95以上.分析此系统的冗余个数和

表1 阶段参数

表2 系统和部件参数

1) 首先采用层次分析法，分析 ω1，ω2，ω3，ω4.依据9标度法并经专家讨论分析得到艇用蓄电池的可靠度、体积、重量和价格间的两两判断矩阵，如表3所示.利用方根法求解，得到ω1=1/2，ω2=1/6，ω3=1/6，ω4=1/6.

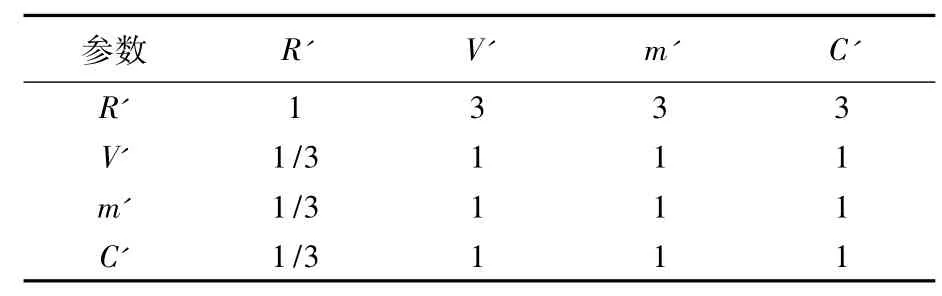
表 3 R'，V'，m'，C'两两判断矩阵

2)综合上述分析，列出基于满意度函数的可靠性冗余优化模型.

式中

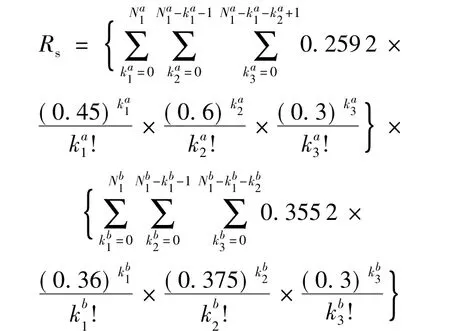
3)采用PSO算法对上述优化模型进行求解.选择粒子数为20，粒子维数为2的粒子群.其进化代数为 100，c1=1.4，c2=1.4，ω =0.4.算法随机运算50次，得到优化结果.图2所示为优化结果迭代图，显然在迭代30次后综合满意度值稳定于0.9348处.图中的每次迭代都进行了取整，所以在微粒值变化不大的情况下迭代结果不会发生改变.

图2 优化结果迭代图

由模型计算可得，某型试验舰船上的电源系统的优化结果如下:

单元a的冗余数为5，单元b的冗余数为3;

系统可靠度为0.9509;

体积为310 dm3;

重量为140 kg;

费用为6100元.

算例表明用PSO算法解决该模型是快速有效的.

5 结 束 语

本文给出的冷贮备PMS的可靠性计算模型和基于综合满意度的可靠性优化模型，有效地解决了冷贮备PMS的可靠性冗余优化问题.但在实际过程中，PMS可靠性冗余优化问题中还存在部件的多模式失效、共因失效、系统单元的多状态、失效率的分布、满意度的多因素等问题，这还需要今后进一步地深入研究.

References)

［1］ Esary J D，Ziehms H.Reliability analysis of phased mission［C］//Proc Conf Reliability and Fault Tree Analysis.Philadelphia:Society for Industrial Applied Mathematics，1975:213－236

［2］ Somotherman M K，Zemoudeh K.A non-homogenous Markov model for phased-mission reliability analysis［J］.IEEE Transactions on Reliability，1989(38):585 －590

［3］ Kim K，Park K S.Phased-mission system reliability under Markov environment［J］.IEEE Transactions on Reliability，1994，43:301－309

［4］ Mura I，Bondavalli A.Hierarchical modeling ＆ evaluation of phased-mission systems［J］.IEEE Tran on Reliability，1999，48(4):360－368

［5］ Bondavalli A，Chiaradonn S，Giandomenico F D，et al.Dependability modeling and evaluation of multiple-phased systems using DEEM［J］.IEEE Trans on Reliability，2004，53(4):509 －522

［6］ Mura I，Bondavalli A，Zang X，et al.Dependability Modeling and evaluation of phased mission systems:a DSPN approach［C］//Proc of the DCCA-7.San Jose:IEEE Computer Society Press，1999:319－337

［7］ Zang X，Sun H，Tribedi K S.A BDD-based algorithm for reliability evaluation of phased mission systems［J］.IEEE Transactions on Reliability，1999，48(1):50 －61

［8］ Xing Liudong，Dugan JB.Analysis of generalized phased mission system reliability，performance and sensitivity［J］.IEEE Transactions on Reliability，2002，51(6):199 －221

［9］ Xing Liudong，Dugan J B.Generalized imperfect coverage phased-mission analysis［C］//Proceedings Annual Reliability and Maintainability symposium.New York:IEEE Press，2002:112－120

［10］ Tang Zhihua，Xu Hong，Dugan J B.Reliability analysis of phased mission systems with common cause failures［C］//Proceedings of the Annual Reliability and Maintainability Symposium.New York:IEEE Press，2005:313 －318

［11］ Tang Zhihua，Dugan J B.BDD-based teliability snalysis of phased mission systems with multimode failures［J］.IEEE Transactions on Reliability，2006，55(2):350 －360

［12］黎放，王志国，李平，等.舰船可靠性管理工程［M］.北京:国防工业出版社，1997:47－48 Li Fang，Wang Zhiguo，Li Ping，et al.Reliability management engineering of warship［M］.Beijing:National Defense Industry Press，1997:47 －48(in Chinese)

［13］ Coelho L S.An efficient particle swarm approach for mixed-integer programming in reliability-redundancy optimization applications［J］.Reliability Engineering and Safety，2009，94(4):830－837

［14］高尚，杨静宇.武器-目标分配问题的微粒群优化算法［J］.系统工程与电子技术，2005，27(7):1250－1252 Gao Shang，Yang Jingyu.Solving weapon-target assignment problem by particle swarm optimization algorithm［J］.Systems Engineering and Electronics，2005，27(7):1250 － 1252(in Chinese)

(编 辑:赵海容)

Reliability optimization of standby phased mission system s based on desirability function

Yu Jian Hu Tao Yang Chunhui

(Department of Management，Naval University of Engineering，Wuhan 430033，China)

A phased mission system to be a success，the system must successfully operate throughout all of the phases.A reliability computativemodel of cold-standby phased mission systemswas proposed based on the reliability computativemodel of cold-standby systems，its components have two states and the time to failure of all the components obeys the exponential distribution.Considering some important effect factors of systems'reliability optimization，the sub-desirability functions of system reliability，system volume，system mass and system cost were built，and their effect modulus were determined through analysis hierarchy process method.Synthesizing these effect factors，a reliability redundancy optimization model of cold-standby phased mission systemswas established based on the synthesis desirability functions.The particle swarm optimization was used to solve the reliability redundancy optimization model.The proposed solutions are verified and illustrated through a three phased cold standby system.The model's rationality and the arithmetic's validity were validated by the experimental results.

redundancy;optimization;reliability analysis;particle swarm optimization

E 92

A

1001-5965(2011)03-0374-05

2010-01-12

总装预研资助项目(1010503010203)

俞 建(1985－)，男，江苏通州人，硕士生，yujian1985@139.com.