测试有效性对软件可靠性验证测试量的影响

李秋英 李海峰 王 健

(北京航空航天大学 可靠性与系统工程学院，北京 100191)

测试有效性对软件可靠性验证测试量的影响

李秋英 李海峰 王 健

(北京航空航天大学 可靠性与系统工程学院，北京 100191)

针对传统软件可靠性验证测试方法均不考虑软件测试性可能会对验证测试用例数量产生影响的现状，提出一种引入测试有效性对软件可靠性验证测试最小量进行改进的方法.分析了软件测试性的定义及其对软件可靠性测试集合的影响，提出软件测试有效性的概念.比较了考虑测试有效性前后软件可靠性验证测试集合在数量上的差异，证明经典统计方法和无先验知识的Bayesian统计推断方法确定的均为假定测试有效性为零情况下的保守估计.提出结合测试有效性的验证测试量的量化表示模型和验证测试方案的改进方法，基于统计故障注入的原理，提出测试有效性的定量评估方法，最后通过示例给出定量评估过程和方法.

软件可靠性;验证;测试;有效性;影响;评估

软件可靠性验证测试(SRDT，Software Reliability Demonstration Testing)作为验证软件可靠性指标的重要决策依据，国内外已取得了一系列研究成果，如TRW验证测试、Bayesian无失效验证测试、单风险序贯测试等［1］.由于需要数量庞大的测试用例或相当长的测试时间，影响了这些验证测试方案在高可靠安全关键软件中的应用.学者们试图降低SRDT所需的测试量，如基于贝叶斯统计推断的 SRDT［2］、分层抽样［3］、程序切片［4］、实验设计［5］、重要度抽样［6］、提高软件输入严酷度［7］、调整 Markov 链使用模型的迁移概率［8］等.上述方法的目的均为在保证置信水平的同时，减少用例量或测试时间.但这些方案无一例外地均未考虑软件测试性这一对软件可靠性测试工作量可能会产生重要影响的因素.

软件测试性是软件的内在属性，是对软件进行有效测试难易程度的一个指标［9－11］.如果软件的测试性好，则通过统计测试来保证软件质量的效果就好;反之，则无法起到有效的保障作用.文献［12－13］通过实验验证了软件测试性对实现软件可靠性目标所需测试用例数量的影响.

本文针对软件测试性进行分析，通过将测试性对测试集合影响的外在表现定义为测试有效性，将测试性与测试集合建立起联系，并将测试有效性引入软件可靠性测试工作量的表示模型中，从理论上证明其对软件可靠性测试工作量的影响，从而对已有验证测试方案进行改进.

1 相关研究

1.1 软件测试性定义

目前最具代表性的软件测试性定义［9－11］是:软件有效测试难易程度的指标，可表示［13］为

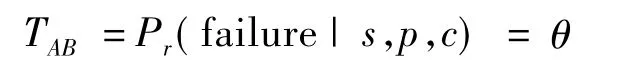
其中，s表示软件规范;p表示程序实现;c表示测试准则;Pr表示概率.软件测试性TAB可理解为:若根据c对软件(s，p)进行充分测试时，软件失效概率(或软件缺陷的检测概率)就是软件测试性的体现.若设软件中包含 r个缺陷 f1，f2，…，fr，则有

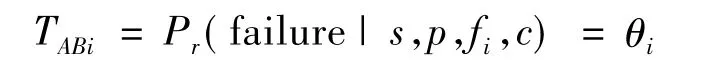
即不同缺陷具有不同的失效概率，此时使用单个缺陷的失效概率表示软件测试性是不准确的，但目前尚未提供测试性的量化模型［13］.

1.2 对现有SRDT方案的分析

1.2.1 经典统计方法TRW的无失效考核方案

根据合同参数软件失效概率指标p0、置信水平α及最大允许的失效数F，计算满足可靠性指标要求所需的验证测试用例数N.

无失效考核方案中不允许发生失效(即F=0)，对于给定的p0，当n个测试用例无失效运行后，对软件失效概率不高于p0的置信度为

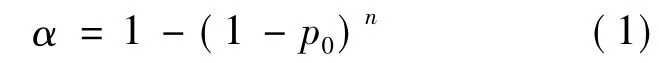
则对于规定的可靠性指标(p0，α)，验证软件达到可靠性指标的最小测试用例数为

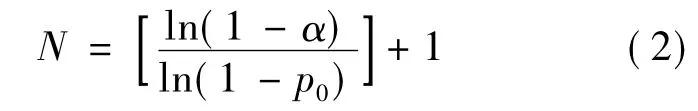
其中，［·］表示对·取整

1.2.2 无先验知识的Bayesian统计推断方法

用β(a，b)来表示失效概率的先验分布密度函数，则在Bayesian框架下，其后验分布也是β分布，则失效概率的先验密度分布函数［14］为

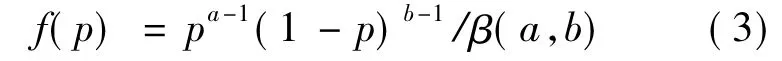
其中，a＞0;b＞0;β(a，b)为 Beta函数，即

当软件执行完n个测试用例、发现r个失效，则失效概率的后验分布为β(a+r，b+n－r)，即

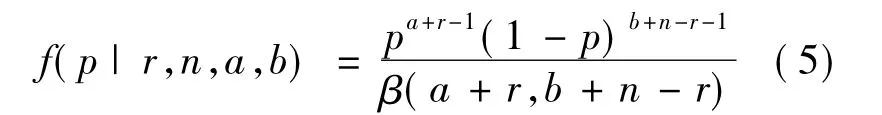
对于无先验的情况，有a=b=1，则有

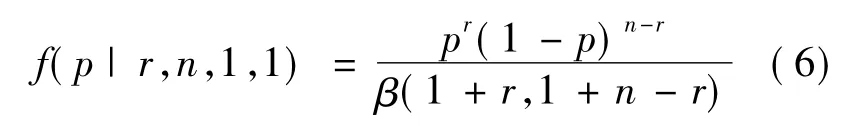
对于给定(p0，α)，当无失效考核时所需要的最小用例数N为满足下式中n的最小整数:

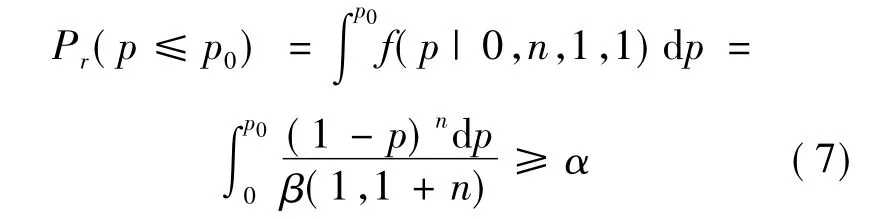
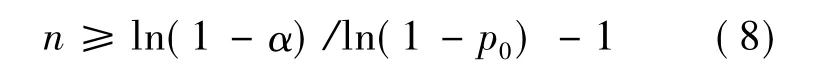
由式(8)可知，所需的最小用例数为

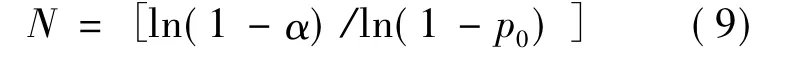
由式(2)和式(9)可知，无论是TRW方案还是Bayesian方案，在确定所需测试用例数时，只依据置信度和可靠性指标，与测试性无关.

2 软件测试有效性定义和影响分析

2.1 软件测试有效性的定义

借鉴文献［15］给出的测试方法有效性定义，给出统计测试集合T的测试有效性的定义:T发现缺陷的测试有效性为在程序中有缺陷的情况下，T发现程序中有缺陷的概率.可表示为:ρT=Pr(测试集合T发现程序P中有缺陷/程序P中有缺陷)假设“程序中有缺陷”是恒成立的命题，则有

ρT=Pr(测试集合T发现程序P中有缺陷).

在一次测试中，该值可以表示为

显然，T的测试有效性是受每一个缺陷fi的测试性影响的，但不同的T发现缺陷的能力常常不同，这点可由不同的T具有不同的覆盖情况，从而发现不同的缺陷而简单验证.

2.2 测试有效性对SRDT测试量的影响分析

设Ω为所有程序P'组成的程序空间，P'是对程序P进行变异生成的任意程序，设PG为对P进行变异生成的完全无错的程序版本.将Ω划分成2个子域A1和A2，其中A1是具有下述属性的程序集合:程序中包含缺陷，且任意缺陷都能被T发现或者程序是无错的，即［16］

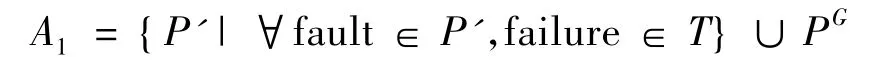
其中，fault∈P'表示 P'中的缺陷;failure∈T表示缺陷fault引起的失效failure能被T发现.

A2是具有下述属性的程序的集合:程序包含缺陷，且所有缺陷都不能被T发现，即

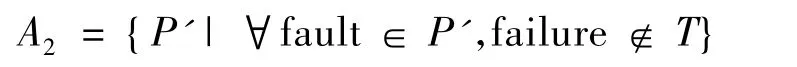
图1给出程序空间的划分，结合测试有效性的概率形式的定义，得Pr(P∈A2|T)=1－ρT.

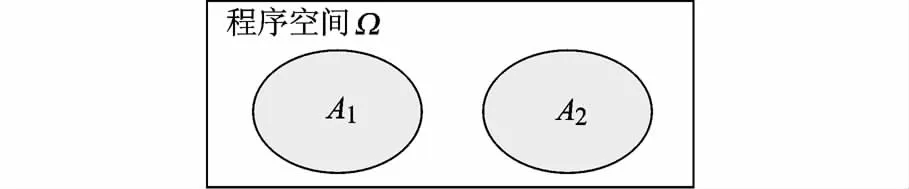
图1 程序空间Ω的划分

假定测试集合T测试程序P的结果为执行N个测试用例，发现0个失效，用符号o表示为:o={N个测试用例执行，发现了0个失效}.现象o出现，可能有下述2种情况:①P∈A1且 P=PG;②P∈A2且具有未知的失效概率∈［0，1］.

设f(θ|o，ρT)表示在出现现象o下的失效密度函数，则有

式中，f(θ|o，ρT)表示观察到现象o、测试有效性为ρT下的条件失效密度函数;Pr(P∈A1)表示程序P属于子域A1的概率，即程序P中有缺陷，且能被T发现的概率;Pr(P∈A2)表示程序P属于子域A2的概率，即程序P中有缺陷，但不能被T发现的概率;δ(0)表示 delta函数［16］，delta分布本身是一个比较特殊的函数，表示如下:

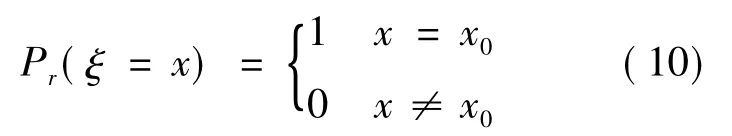
其概率密度函数表示为

此处用于表示

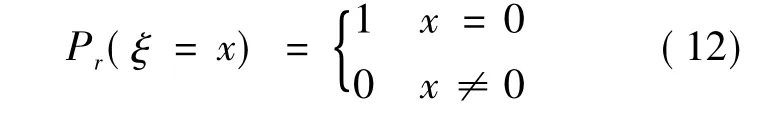
即δ(0)表示此时的条件概率密度;β［1，N+1］(θ)表示N个测试用例执行下0个失效的后验密度.

对于给定的(p0，α)，当不容忍失效时，所需最小用例数N为满足下式中n的最小整数:

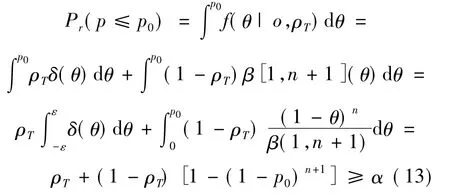
化简上式可以得到

设 ρT=0，则有

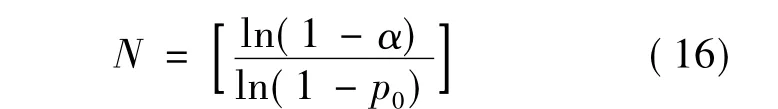
不难看出式(16)与式(9)相同，这表明Bayesian方案中将测试有效性简化为0.

下面对式(15)进行分析，令

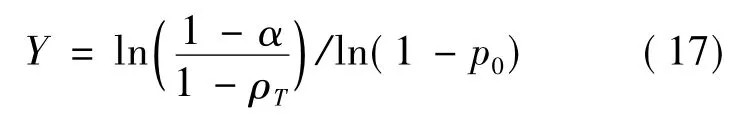
两边同时对ρT求导，则有

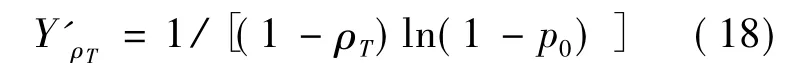
因为0≤ρT＜1，0 ＜p0＜1，所以 Y'ρT＜0，即 Y 是 ρT的减函数，随着ρT增加Y减小.

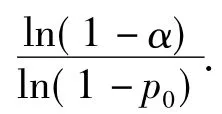
工程实践中进行无失效考核往往需要数目庞大的测试用例数量［17］，原因之一是:对于不同的软件来说，测试有效性越高，测试用例的缺陷探测性能越好，此时所需的测试用例量就少;反之，所需的测试用例量就大.但现有方案不考虑软件在测试性方面的不同，进而不考虑测试集合在不同软件的测试有效性的不同，而是把所有测试集合在软件上的测试能力都忽略为0，从而从最保守估计的角度确定测试集合量的大小，无疑在某些情况下浪费了大量的测试用例.

3 测试有效性的定量估计

3.1 基本原理

假设P是Ω的一个随机实现，利用统计故障注入法来得到ρT的定量估计，具体内容包括:

1)在P 的基础上生成若干变异程序［18－20］P'，令P'中的缺陷具有与P相同的统计分布特征，这样P'中的缺陷就包括原程序P中的缺陷和新植入的缺陷.由于原P中的缺陷不能被测试集合T检测出来，这样原来的缺陷就不会对T的测试有效性产生贡献，因此T在P'上的测试情况就相当于其在无错版本PG基础上加随机新植入缺陷集合(记为FSi)上的测试情况，即PG+FSi.观察T在FSi上的测试情况相当于T在以PG为基础而随机注入缺陷所得版本上的测试情况.由于P本身就是一个以无错版本PG为基础而包含随机错误的程序，所以观察T在FSi上的测试情况就相当于T在P上的测试情况.

2)将随机注入缺陷FSi得到的变异程序P'的集合分为2个子集，其中子集B1表示能够被T检测出错误的变异程序的集合，B2表示不能够被T检测出错误来的变异程序的集合，依据图1所示的程序空间的划分，计算出变异程序P'落入B1的概率，即求得测试有效性的定量估计值.

3.2 基本假设

下面给出上述原理成立所需要的一些基本假设:①所有植入缺陷引起的失效都能够在输出端被清楚地观测到;②在故障注入之前，原程序P中的缺陷不能被T检测出来;③每一个植入缺陷都是相互独立的，植入的缺陷是与失效现象一一对应的.

3.3 构造变异程序

依据统计分布规律在人为植入故障的基础上构造变异程序P'，具体步骤如下:

1)假设原程序的故障数服从某一概率分布，具体可以依据一些先验信息来确定;

2)根据分布特征，在所有植入故障的集合中按照该统计分布随机抽样得到Mi个缺陷;

3)通过故障注入法将这Mi个缺陷注入到原程序P中，则得到变异程序P'.

以泊松分布为例对上述过程进行说明:

1)设程序中的故障数服从泊松分布，根据泊松分布的特点，需要利用参数λ进行泊松分布函数的构造，此时的λ代表程序中潜藏缺陷数目的平均值M^.对于程序P来说，M^可以根据程序的规模、复杂度等信息事先估计得到［21］.

2)获得参数λ的估计值后，可以得到此分布的概率密度函数，如下式所示:

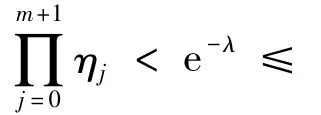
4)得到Mi的一个随机抽样值m后，从所有植入缺陷集合中随机抽取m个缺陷通过故障注入技术注入到程序P中.植入的过程为:假定已经事先设计了N个错误，且满足N≫λ，且对每一个故障进行编号 1，2，…，N.在［0，1］区间内，随机生成 m 个随机数 η1，η2，…，ηm，令 Ki= ［(N －1)ηi］+1，i=1，2，…，m.这样便得到 m 个故障编号K1，K2，…，Km.如果m个故障编号中有重复编号Ki，且重复次数为k，则只保留一个这样的故障编号，删除其他重复故障编号，重新再生成k－1个随机数，按上述方法重新得到k－1个故障编号，直到最后得到m个不同的故障编号为止.再根据这m个故障编号把对应故障注入程序，即得到变异程序P'.

5)重复3)，4)，直至得到F个变异程序.F可以尽可能的大，也可以根据实际情况进行确定，但理论上讲，F越大，意味着最后计算得到的ρT值越接近于真实值.

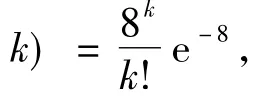
3.4 利用测试结果确定P'的分类

设FSi表示最后得到的第i个P'i的植入缺陷集合，i=1，2，…，F.每个错误集合 FSi包含的错误数量为Mi.利用T对P'i进行测试时，测试过程中会出现以下3种情况:

1)顺序执行T中的测试用例，直到有一个失效产生，并且这个失效可以追踪到新植入的缺陷集合FSi中的某个缺陷，则说明FSi能够被T检测出来，即此P'i属于B1，记φ(FSi)=1;

2)顺序执行T中的所有测试用例，但是没有失效产生.这样，缺陷集合FSi不能被T检测出来，即此 P'属于 B2，记 φ(FSi)=0;

3)顺序执行T中的测试用例，直到有一个失效产生，并且对这个失效追踪时发现，它不是由新植入的缺陷集合FSi中的任何一个缺陷产生的，那么由假设可知，它一定是新植入的缺陷与原程序P中的一个真实缺陷之间相互作用产生的相关错误，不满足统计故障注入独立性的特点.因此，将此缺陷从N个缺陷组成的缺陷集合中排除，并重新生成一个新的缺陷，对N个缺陷重新进行编号，重复3.3节中的步骤3)～5)，重新生成F个P'，并重新利用T对P'i进行测试，利用测试结果确定P'的分类.

重复上述过程，直至T对所有F个变异程序都完成测试，则可得T的测试有效性ρT如下:

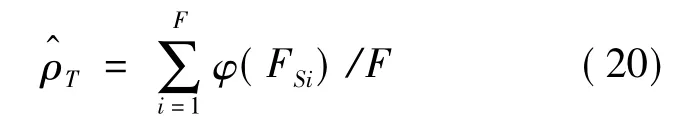
式中，分子表示能够被T检测出缺陷的变异程序的个数，即B1中包含的程序数目.

4 测试有效性对SRDT测试量改进

4.1 验证测试方案的改进

综上，考虑测试有效性的影响，对无失效考核的SRDT方案进行改进，内容如下:①通过操作剖面随机生成n个测试用例，一般来说，n≥50;②用该n个测试用例执行软件时，未发生任何失效;③根据3.3和3.4节介绍的方法，获得测试有效性ρT的定量估计值;④利用式(15)确定考虑了测试有效性影响的可靠性验证测试所需的测试用例数量N;⑤通过操作剖面随机生成N个测试用例，并执行上述N个测试用例;⑥在测试执行过程中，如果N个测试用例中发生了失效，则拒收;否则接收.

4.2 可靠性参数的估计

离散型软件的可靠性评估是通过失效概率或成功率来完成的，此处定义失效概率为

其中，n为发生失效的测试用例数;N为测试用例总数.p的置信水平为1－α的置信限［23］为

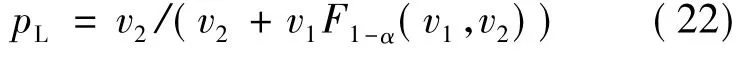
其中，v1=2(N －n+1);v2=2n.

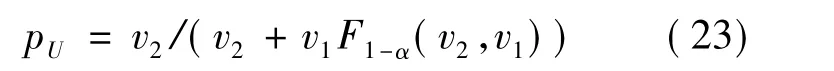
其中，v1=2(N－n);v2=2(n+1).

当n=0时，失效概率单侧置信上限［24］为

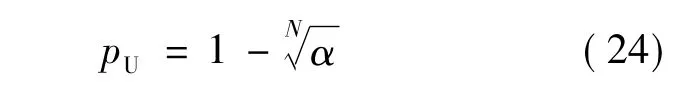
连续型软件的可靠性评估是通过失效率来完成的，失效率的上限值［25］如下式所示:

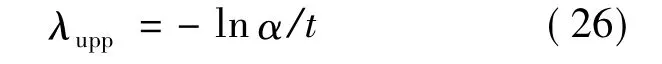
4.3 考虑测试有效性的优越性

表1给出不同(p0，α，ρT)下无失效考核的测试用例量N.

如果待验证的指标为(p0，α)=(10－4，0.99)，按照 TRW 方案需要的测试用例数为46050，Bayesian方案需要测试用例数为46 049.而对于考虑测试有效性的Bayesian方案，当假定测试有效性ρT=0.5时，所需要的测试用例数为39118，测试用例数减少了 15.1%;假定 ρT=0.9时，所需要的测试用例数为23024，测试用例数则减少50%;所需测试用例数显著下降.所以，考虑测试有效性的Bayesian方案对于减轻测试负担是非常有效的，尤其在P0非常小的情况下.

5 结 束 语

本文从软件测试性的角度出发，分析了其对软件可靠性测试用例集合的影响，提出了测试有效性的概念.分析了测试有效性对于SRDT方案中测试量的影响，给出了测试量的量化表示模型，并比较了具有不同测试有效性的测试集合在数量上的差距，证明了TRW方案和Bayesian方案给出的测试量都是在假定测试有效性为零的情况下的保守估计，给出了统计故障注入方法下的测试有效性的定量估计方法和在该方法指导下改进的可靠性验证测试方案及可靠性评估方法.

本文认为测试有效性对于改进SRDT方法、优化测试集合、缩小验证测试工作量，提高测试效率具有重要的意义，当然，如果在测试用例集合选择时，能够优先选用测试有效性高的测试用例集合，既可以大大降低测试工作量，也为一些超高可靠软件的SRDT提供了可能.

References)

［1］李秋英，姜梦岑.软件可靠性验证测试最小测试量的必要条件［J］.北京航空航天大学学报，2010，36(2):239 －243 Li Qiuying，Jiang Mengcen.Analysis of necessary condition for minimal software reliability demonstration test suite［J］.Journal of Beijing University of Aeronautics and Astronautics，2010，36(2):239－243(in Chinese)

［2］覃志东，雷航，桑楠，等.连续执行软件可靠性验证测试方法［J］.计算机科学，2005，32(6):202 －207 Qin Zhidong，Lei Hang，Sang Nan，et al.Reliability demonstration testingmethod for continuous execution software［J］.Computer Science，2005，32(6):202 －207(in Chinese)

［3］ Andy P，Wassim M，Yolanda M.Estimation of software reliability by stratified sampling［J］.ACM Transactions on Software Engineering and Methodology，1999，8(3):263 －283

［4］ Cukic B.Accelerated testing for software reliability assessment［C］//Biljanovic P.21st Annual International Conference MIPRO'98.Washington DC:IEEE Com Soc，1998:124 －129

［5］ Alam S，Chen H，Ehrlich WK，et al.Assessing software reliability performance under highly critical but infrequent event occurrences［C］//Philip G.8th ISSRE.Los Alamitos:IEEE Comp Soc，1997:294 －303

［6］ Hecht M，Hecht H.Use of importance sampling and related techniques to measure very high reliability software［C］//Joel S.Aerospace Conference Proceedings.Montana:IEEE Aerospace and Electronics Systems Soc，2000:533 －546

［7］ Tang D，Hecht M，Miller J.MEADEP and its applications in evaluating dependability for air traffic control systems［C］//Schueppert.Proceedings of the Annual Reliability and Maintainability Symposium Anaheim.Washington DC:IEEE Reliability Society，1998:19 －22

［8］颜炯，王戟，陈火旺.基于重要度抽样的软件统计测试加速［J］.计算机工程与科学，2005，27(3):64 －66 Yan Jiong，Wang Ji，Chen Huowang.Software statistical test acceleration based on importance sampling ［J］.Computer Engineering and Science，2005，27(3):64 －66(in Chinese)

［9］ IEEE SA 610.12-1990 IEEE standard glossary of software engineering terminology，［S］

［10］ ISO/IEC9126-91 Software engineering-product quality［S］

［11］ Hamlet D，Voas J.Faultson its sleeve:amplifying software reliability testing［C］//Thomas O.1993 ACM SGSOFT.Cambridge:ACM Society，1993:89 －98

［12］ Chen W，Untch R H，Rothermel G.Can fault-exposure-potential estimates improve the fault detection abilities of test suites?［J］.Journal of Software Testing，Verification，and Reliability，2002，4(2):197 －218

［13］赵亮，王建民，孙家广.软件易测性和软件可靠性关系研究［J］.计算机学报，2007，30(6):986 －991 Zhao Liang，Wang Jianmin，Sun Jiaguang.Study on the relationship between software testability and reliability［J］.Chinese Journal of Computers，2007，30(6):986 －991(in Chinese)

［14］ Miller KW，Morell L J，Noonan R E.Estimating the probability of failure when testing reveals no failures［J］.IEEE Transactions on Software Engineering，1992，18(1):33 －43

［15］ Kuball S，Hughes G，May J，et al.The effectiveness of statistical testing when applied to logic systems［J］.Safety Science，2004，42(5):369－383

［16］ Kuball S，May J.Test-adequacy and statistical testing combining different properties of a test-set［C］//Stephanie K.15th ISSRE.Washington DC:IEEE Com Soc，2004:161 －172

［17］覃志东，雷航，桑楠，等.安全关键软件可靠性验证测试方法研究［J］.航空学报，2005，26(3):334 －339 Qin Zhidong，Lei Hang，Sang Nan，et al.Study on the feliability demonstration testing method for safety critical software［J］.Acta Aeronautica et Astronautica Sinica，2005，26(3):334 － 339(in Chinese)

［18］ Woodward M R，Halewood K.From weak to strong，dead or alive，an analysis of some mutation testing issues［C］//2nd Workshop on Software Testing，Verification and Analysis.Washington DC:IEEE Com Soc，1988:152 －158

［19］ Agrawal H，Demillo R，Hathaway B，et al.Design of mutant operators for the C programming language［R］.SERC-TR-41-P，2006

［20］赵性颂，顾斌.变异测试在嵌入式软件中的应用［J］.微计算机信息，2009，25(11－2):87－88 Zhao Xingsong，Gu Bin.The application of mutation testing in embedded software ［J］.Microcomputer Information，2009，25(11－2):87－88(in Chinese)

［21］ Lyu M R.Handbook of software reliability engineering［M］.New York:McGraw Hill，1996

［22］杨为民，盛一兴.系统可靠性数字仿真［M］.北京:北京航空航天大学出版社，1990:52－54 Yang Weimin，Sheng Yixing.System reliability digital simulation［M］.Bejing:Beijing University of Aeronautics and Astronautics Press，1990:52 －54(in Chinese)

［23］GB/T 4087.2-1983 数据的统计处理和解释［S］GB/T 4087.2-1983 Statistical interpretation of data［S］(in Chinese)

［24］GB 4087.3-85 数据的统计处理和解释二项分布可靠度单侧置信下限［S］GB 4087.3-85 Statistical interpretation of data One-sided reliability confidence lower limit［S］(in Chinese)

［25］ Kececioglu D.Reliability and life testing handbook［M］.NJ:Prentice Hall，Englewood Cliffs，1993:722 － 724

(编 辑:娄 嘉)

Effects of software test efficiency on software reliability demonstration testing effort

Li Qiuying Li Haifeng Wang Jian

(School of Reliability and Systems Engineering，Beijing University of Aeronautics and Astronautics，Beijing 100191，China)

To solve the problem that in the traditional software reliability demonstration testing(SRDT)，software testability was not considered as one of the possible influence factors on test effort，a method which introduced test efficiency to improve the quantity model of minimal sample size in SRDT was put forward.The definition of software testability and its effect on software reliability test suite were analyzed.The concept of test efficiency was proposed.The difference between the numbers of test cases with different test efficiency and whether efficiency is considered were compared.It was demonstrated in detail that the traditional method and the Bayesian method with no prior knowledge are all the conditions where the testefficiency equaled to zero，so both the methods gave the most conservative value.The improved method combined with the testefficiency was recommended.Based on the principle of statistical fault injection，the quantitative estimation method of testefficiency was proposed and the process and the estimation method were shown by a case study.

software reliability;demonstrations;testing;efficiency;effects;estimation

TP 311

A

1001-5965(2011)03-0325-06

2010-10-11

国防科技工业技术基础科研项目(Z132010B001)

李秋英(1973 －)，女，黑龙江大庆人，讲师，li_qiuying@buaa.edu.cn.