大型碳纤维桁架结构模态试验及特性

陶国权 卫宇晨 吕明云 武 哲

(北京航空航天大学 航空科学与工程学院，北京 100191)

大型碳纤维桁架结构模态试验及特性

陶国权 卫宇晨 吕明云 武 哲

(北京航空航天大学 航空科学与工程学院，北京 100191)

基于随机子空间识别方法，采用自然脉动试验研究了大尺度、轻质高强承力型碳纤维复合材料桁架结构的模态特性.基于该桁架结构本身的特点，提出了3个基本假设，结合实际应用中桁架结构的约束条件，设计了大型碳纤维复合材料桁架的模态试验方案，并对试验结果进行了详细分析，总结了其频率特性、阻尼特性及振型特点.结合锤击法试验和有限元方法，对试验结果进行对比分析，结果表明3个基本假设合理，试验方案有效，试验分析结果可靠.研究结果可应用于浮空器结构设计和健康监测.

大型碳纤维桁架;随机子空间识别法;模态测试;有限元分析

平流层浮空器现已成为各国研究的热点，美国、加拿大、日本、韩国、英国、德国和以色列等国正在积极开展相关研究.大尺度、轻质高强承力型复合材料桁架结构为浮空器提供支撑平台和各种载荷设备的安装平台，研究其动态特性对浮空器的发展具有重要意义.

为了研究浮空器桁架结构在风、螺旋桨等动载作用下的行为，防止结构系统和其他分系统发生共振现象，需要掌握其动力特性:固有频率、振型和阻尼.碳纤维是各向异性复合材料，分析其桁架结构的动态特性和有限元建模较为复杂.通过模态参数识别研究提供碳纤维桁架结构的动力特性参数，同时为有限元分析提供依据.

传统的模态参数识别方法是通过频响函数进行模型拟合而获得模态参数，它要求结构的输入和输出都是已知的.但对于尺寸巨大的浮空器桁架结构，通常无法用合适的激励方式使结构产生整体振动(即无输入数据)，这使得基于频响函数的模态参数识别方法难以适用.

针对以上问题，采用自然脉动试验［1－5］和随机子空间识别方法［6－8］研究桁架结构的模态特性.本文提出了用于分析大型碳纤维复合材料桁架结构的3个合理的基本假设，在该假设基础上，结合约束条件，设计了桁架模态试验方案，得到了大型碳纤维桁架结构的模态特性:频率、阻尼和振型.

1 随机子空间法的原理

对于线性多自由度系统，其运动微分方程为

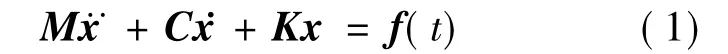
式中，f(t)为n维激振力向量;x，x·，x··分别为n维位移、速度和加速度响应向量;M，K，C分别为结构的质量、刚度和阻尼矩阵.其离散状态空间方程表示如下:

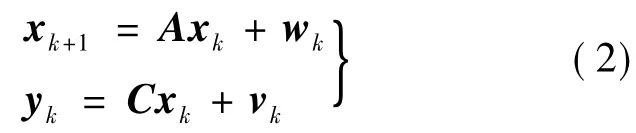
式中，xk是n维状态向量;yk是n维输出向量，n为响应点数;wk和vk分别是均值为0的输入和输出白噪声;A和C分别表示n×n阶状态矩阵和n×n阶输出矩阵，系统的特性完全由特征矩阵A的特征值和特征向量表示.特征矩阵A的特征值分解如下:

由矩阵Λ得到离散的特征值λr，可用下式求得系统的特征值μr:

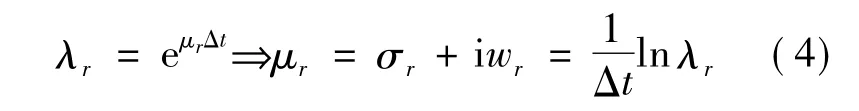
式中，σr是阻尼因子;wr是r阶固有频率;阻尼比ξr由下式给出:

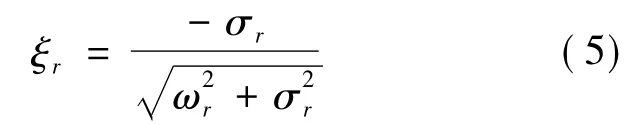
第r阶模态的阵型Ψr是矩阵Φr的系统特征向量φr的可观部分，表示如下:

可见，只要求出AC便可进行模态参数的识别.

下面是利用输出相应的相关函数和Hankel矩阵来求AC.相关函数Rk表示成下式:

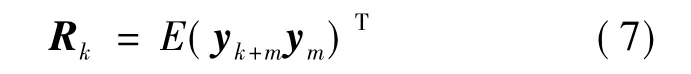
用相关矩阵Rk建立p行和q列的Hankel矩阵(p≥q)，如下:

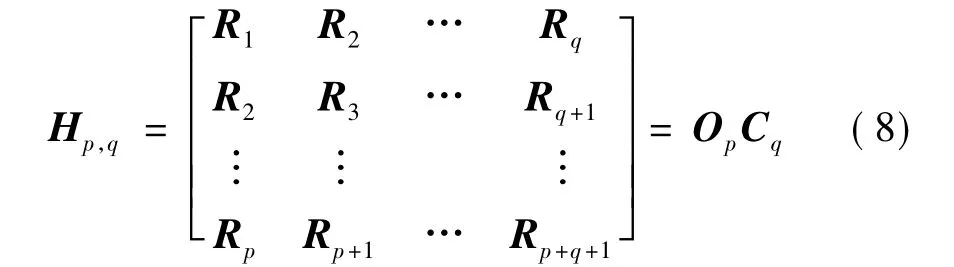
式中，Op，Cq分别是离散状态空间方程的p阶可观矩阵和q阶可控矩阵，分别为

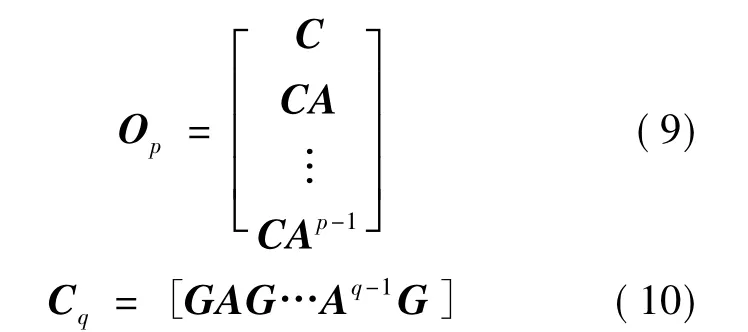
式中

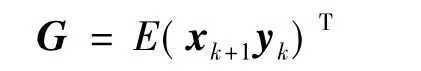
对Hankel矩阵进行奇异值分解，再根据矩阵Op，Cq的特点，可以求得矩阵 A，C，由此识别出系统模态参数.

2 试验方案

2.1 碳纤维桁架结构

试验桁架为浮空器整体结构中的一个典型部件，由碳纤维杆件通过金属连接件组合而成，分为主杆、隔框杆和斜杆，主杆为6m长的连续杆件，截面形状为正三角形，外接圆半径为550mm，如图1所示.

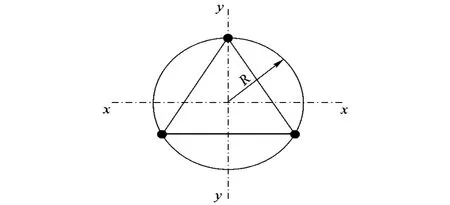
图1 桁架截面

试验桁架总长为30m，由28个隔框和2个三角锥组成，如图2所示.碳纤维杆件具体尺寸与铺层方式如表1所示，桁架结构的一个侧面作为试验及分析的参考面.

图2 试验桁架结构

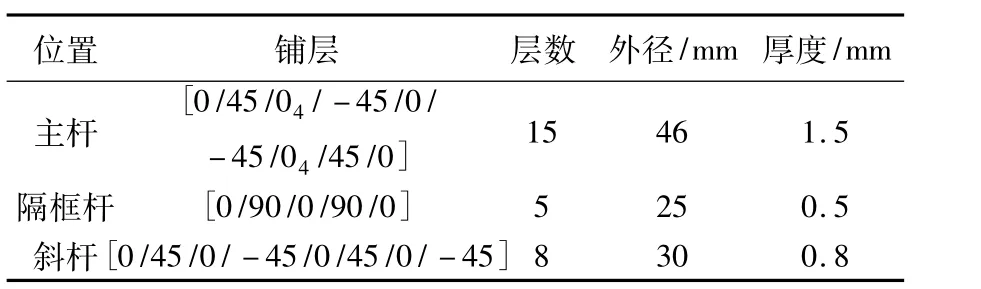
表1 碳纤维杆件的设计参数

2.2 约束条件

本文采用桁架两节点水平自由吊挂的方式作为结构试验的边界条件，吊挂形式为空间桁架的一个平面与地面平行.吊挂点选择在主要频率范围内的振型节点上，以减小约束形式对测量结果的影响.参考有限元分析的结果，在桁架的第7框和第21框主杆节点位置用弹性绳吊挂结构，具体吊挂形式如图3所示.

图3 弹性绳约束点

2.3 3个基本假设

桁架属于中心对称结构，其每一个隔框截面相比径向方向有足够的面内刚度，基于桁架结构以上的特点，提出以下3个基本假设:

1)沿垂直于桁架的任意一个参考面方向吊挂结构得到的模态分析结果一致;

2)在桁架振动时隔框截面形状保持不变;

3)不考虑隔框杆、斜杆的弯曲振动.

2.4 传感器布置方案

在上述3个基本假设的基础上，设计试验传感器的布置方案.基于假设1)，试验过程中测量参考面方向和垂直于参考面方向的加速度值;基于假设2)，在参考面外的隔框节点测量平行于参考面方向的加速度;基于假设3)，在桁架节点处布置加速度传感器.具体布置方案为桁架每隔2m在隔框截面上布置一组传感器，两端三角锥布置2个.典型截面传感器的布置方式与方向如图4所示，重力方向竖直向下.

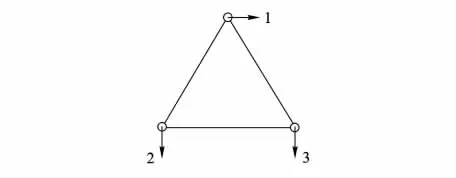
图4 截面传感器布置示意图

3 试验过程

选择微风天气，按照上述试验方案采用自然脉动法对表面涂有银白色防辐射材料的碳纤维复合材料桁架结构进行试验数据采集，采样频率为102.4Hz，采用自由触发方式，采集时间为30min，试验现场如图5所示.

试验过程中11～14号加速度传感器采样全程波形如图6所示.

图5 自然脉动法测试试验

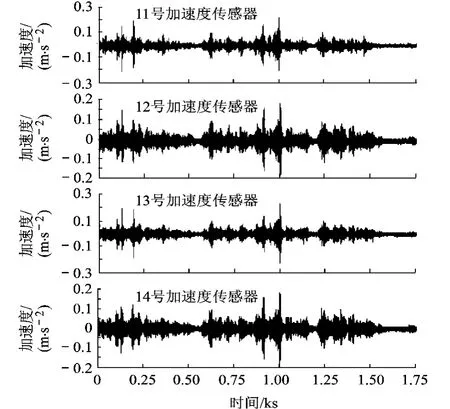
图6 11～14号传感器加速度响应

利用随机子空间法对自然脉动法的测试数据进行分析，得出桁架结构的前10阶固有频率和阻尼如表2所示，前4阶振型如图7所示.由以上分析结果可知，桁架结构的1阶频率为7.08 Hz，9～10阶频率值比较接近，其余各阶频率值变化较大，结构的阻尼比较稳定，结构前10阶阵型中，1阶阵型为弯曲，其后弯曲与扭转交替出现.

完成脉动法试验数据采集后进行锤击法模态测试试验，试验频率结果分析如表3所示.

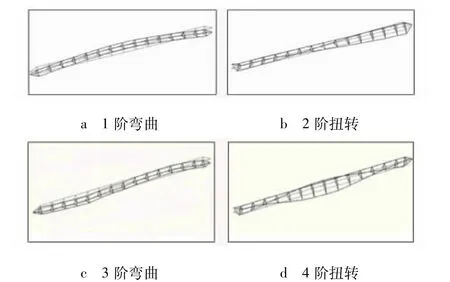
图7 试验得结构1～4阶振型图

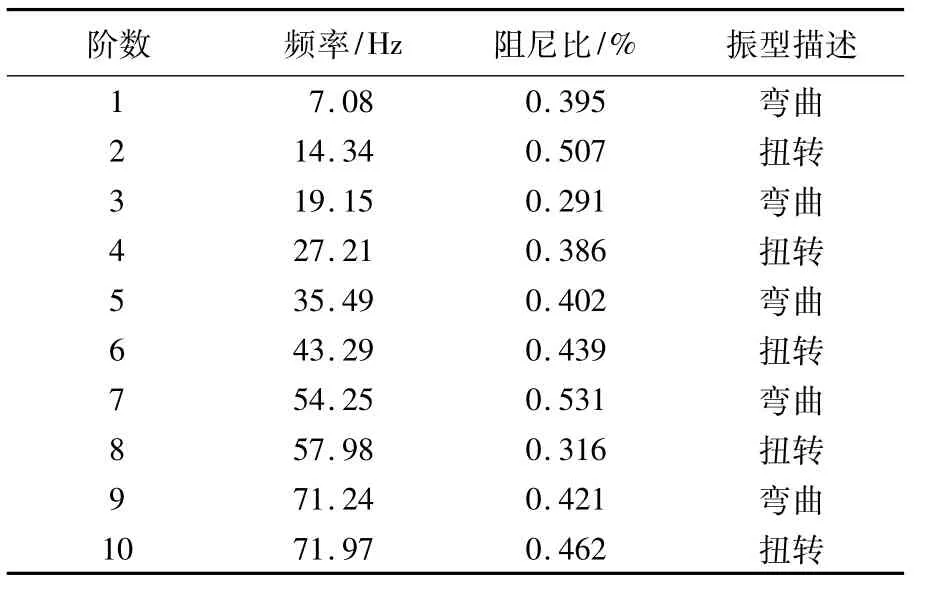
表2 测试得结构的频率及阻尼比

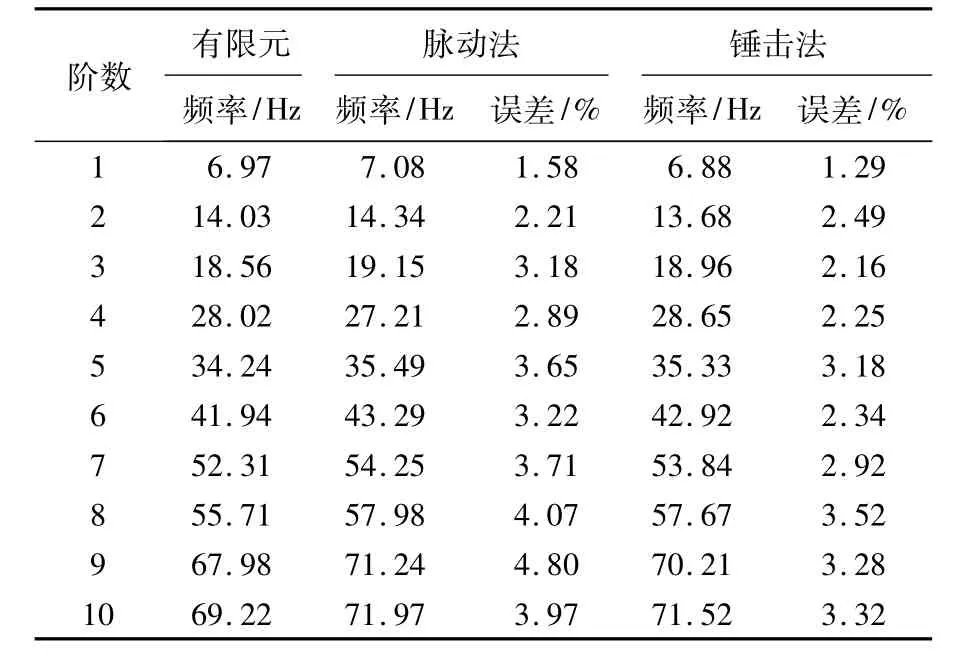
表3 试验结果与有限元分析结果比较

4 复合材料桁架有限元分析验证

为了验证利用随机子空间识别法分析碳纤维复合材料桁架结构自然脉动模态试验结果的正确性，将脉动法与锤击法的试验结果和有限元分析的结果进行比较，如表3所示.

有限元分析碳纤维桁架结构前4阶振型如图8所示.

图8 有限元分析结构前4阶振型

由表3可知2种模态试验测试结果和有限元分析的各阶频率误差均小于5%，比较图7和图8，脉动法试验和有限元分析得出的结构振型基本一致，说明大型碳纤维桁架结构脉动法模态测试试验结果是可信的，且精度较高.

5 结论

利用随机子空间识别方法对大型碳纤维桁架结构的脉动试验结果进行模态分析，得出前10阶频率、阻尼和振型，与锤击法的试验结果和有限元分析结果吻合较好，说明其试验结果是可信的，测试方法是有效的，有限元分析模型和计算方法是可行的.通过试验结果说明对大型碳纤维桁架结构在模态测试试验中提出的3个假设是合理的.利用3个假设能在不影响试验测试精度的前提下简化传感器的布置方案.自然脉动法和随机子空间识别相结合的方法为浮空器大型复合材料桁架结构的动态特性测试提供了一种有效的途径，也为浮空器结构设计和系统健康监测提供了基础.

References)

［1］ Wilson JC，Liu T.Ambient vibration measurements on a cablestayed bridge［J］.Earthquake Engineering ＆ Structural Dynamics，1991，20(8):723 －747

［2］ Gao Y，Spencer B F.Damage localization under ambient vibration using changes in flexibility［J］.Earthquake Engineering and Engineering Vibration，2002，1(1):136 －144

［3］ Bernal D，Gunes B.Observer Kalman and subspace identification of the UBC benchmark structural model［C］//Proceedings of the 14th ASCE Engineering Mechanics Conference.Austin:［s.n.］，2000:21 －24

［4］ Kaminski PC.The approximate location of damage through the analysis of natural frequencieswith artificial neutral networks［J］.Proceedings of the Institution of Mechanical Engineers，Part E:Journal of Process Mechanical Engineering，1995，209(E2):117－123

［5］ James G H Ⅲ，Carne T G，Lauffer JP.The natural excitation technique for modal parameter extraction from operating structures［R］.SAND92-1666，1993

［6］ Van Overschee P，De Moor B.Subspace identification for linear systems:theory，implementation and applications［M］.Dordrecht，Netherlands:Kluwer Academic Publishers，1996

［7］续秀忠，华宏星，陈兆能.基于环境激励的模态参数辨识方法综述［J］.振动与冲击，2002，21(3):1 －5 Xu Xiuzhong，Hua Hongxing，Chen Zhaoneng.Review ofmodal identification method based on ambient excitation［J］.Journal of Vibration and Shock，2002，21(3):1 －5(in Chinese)

［8］肖祥，任伟新.实时工作模态参数数据驱动随机子空间识别［J］.振动与冲击，2009，28(8):148 －153 Xiao Xiang，Ren Weixin.Improved data-driven stochastic subspace identification of online operationalmodal parameters［J］.Journal of Vibration and Shock，2009，28(8):148 －153(in Chinese)

(编 辑:李 晶)

Modal tests and properties analysis on truss structure of large scale carbon fiber

Tao Guoquan Wei Yuchen Lümingyun Wu Zhe

(School of Aeronautic Science and Engineering，Beijing University of Aeronautics and Astronautics，Beijing 100191，China)

Based on stochastic subspace system identification method，the modal properties of the truss structure of large scale，lightweight，high strength，and force bearing type carbon fiber composites were investigated by ambient excitation.On basis of the characteristics of the truss structure itself，three fundamental assumptions were forwarded.In conjunction with the constraint conditions of the truss structure in practical applications，amodal test scheme for the truss of large scale carbon fiber composites was designed.Through detailed analysis of the test results，the characteristics of frequency，damp，and vibration mode were summarized.By hammer impacts test and finite element method，the test results were comparatively analyzed.It is proved that the three fundamental assumptions are reasonable，the test scheme is effective，the analytical results of the test are reliable.The research results are of essential meaning to the design of aerostat structures and their health monitoring.

truss structure of large scale carbon fiber;stochastic subspace system identification method;modal test;finite element analysis

V 214.8

A

1001-5965(2011)03-0316-04

2010-11-05

陶国权(1983－)，男，浙江绍兴人，博士生，ac97531@163.com.