鸭式旋翼/机翼飞行器转换末段气动特性
2011-03-15李毅波马东立
李毅波 马东立
(北京航空航天大学 航空科学与工程学院,北京 100191)
牛凌宇
(北京系统工程研究所,北京 100101)
鸭式旋翼/机翼飞行器转换末段气动特性
李毅波 马东立
(北京航空航天大学 航空科学与工程学院,北京 100191)
牛凌宇
(北京系统工程研究所,北京 100101)
采用数值模拟方法研究鸭式旋翼/机翼(CRW,Canard Rotor/Wing)飞行器在转换过程末段,旋翼转速极低时全机气动特性变化规律及其产生原因.给出了旋翼旋转一周时,全机气动力、气动力矩、焦点位置变化规律,对此布局形式,转换过程末段全机升力、阻力变化幅度可达10.7%,3.7%,焦点可移动0.6m.研究显示:旋翼处于前后不对称流场及旋翼处于不同方位角时对机体的不对称干扰是气动力与气动力矩变化原因,旋翼与平尾升力线斜率变化、旋翼自身焦点位置变化导致了全机焦点移动.
鸭式旋翼/机翼飞行器;气动特性;流场干扰;飞行模式转换
鸭式旋翼/机翼(CRW,Canard Rotor/Wing)飞行器是一种新型垂直起降、高速巡航飞行器,其主要特征是具有一副可停转旋翼,旋翼可高速旋转为垂直起降提供拉力,又可锁定成固定翼为高速巡航提供升力.CRW飞行器与高速直升机、倾转旋翼飞行器相比,具有更宽的飞行包线,在军民用领域的应用前景十分广泛[1],但由于CRW飞行器存在空气动力学/飞行动力学/飞行控制系统的复杂耦合,其进入实用化还需开展大量研究.
美国从20世纪90年代初开始对CRW飞行器展开系统地理论与实验研究,1998—2005年进行了X-50A“蜻蜓”项目,演示验证CRW飞行器关键技术.韩国航空研究院对CRW飞行器也开展了研究[2-3].近几年来,国内也对 CRW 飞行器相关技术进行了研究,主要集中在喷气旋翼的研究上[4-5],对转换过程气动特性的研究尚处于空白.
CRW飞行器转换过程气动特性具有强烈的非定常与非线性特点,是CRW飞行器研究的重点.转换过程可分为前、中、末3个阶段,转换前段,鸭翼与平尾处于竖起状态,旋翼承担绝大部分升力,全机气动特性主要受旋翼流场影响.转换中段,鸭翼与平尾承担的升力逐渐增大,旋翼升力逐渐减小,全机气动特性受旋翼流场与来流流场综合影响,非定常气动力表现为与旋翼旋转相应的周期性高频振荡.转换末段,鸭翼与平尾承担全部升力,旋翼总距为0,转速极低,此时全机气动特性主要受来流流场影响,与转换前段与中段相比,非定常气动特性及其机理存在较大差别[6].研究转换末段气动特性对CRW飞行器从直升机模式向固定翼模式的平稳安全转换具有重要意义.
本文用数值方法模拟CRW飞行器处于转换过程末段,旋翼转速极低,鸭翼与平尾产生全部升力情况下,全机气动力、气动力矩及焦点位置随旋翼旋转变化规律,并分析其变化原因.
1 分析模型与方法
1.1 几何模型
CRW飞行器几何外形与坐标选取如图1所示.采用三翼面布局形式,从前至后分别为鸭翼、旋翼/机翼、平尾.鸭翼与平尾在起降及转换前段处于竖起状态,以减小旋翼拉力损失,转换末段两者承担全部升力.旋翼为右旋旋翼,定义旋翼处于y轴正方向所在半平面时为右旋翼,与之相对的为左旋翼.为了防止旋翼停转后须将一侧机翼翻转的情况,保证转换过程平稳,旋翼采用无弯度椭圆翼型.
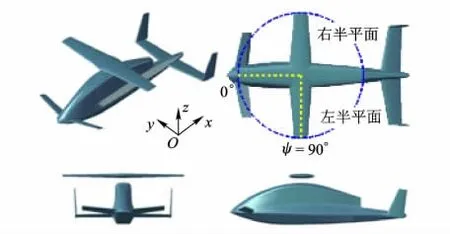
图1 CRW飞行器
转换过程末段,鸭翼襟翼偏转角20°,全动鸭翼偏转角14°,平尾偏转角10°,保证力及力矩平衡,见表1.来流迎角0°,来流马赫数 Ma=0.197,雷诺数Re=2.5×106,参考面积为旋翼面积.

表1 转换末段翼面偏转角度 (°)
1.2 数值计算方法
转换过程末段,旋翼转速极低,桨尖速度相对于来流速度很小,分析时可将旋翼固定于一系列方位角位置,研究每个方位角下全机气动特性.
采用有限体积法求解三维可压雷诺平均N-S(Navier-Stokes)方程,三维任意坐标系下的N-S方程[7]为
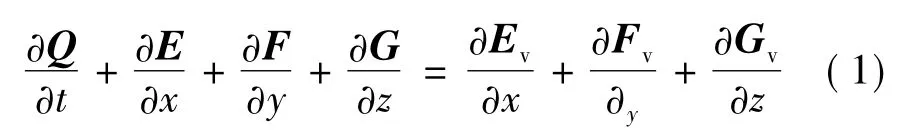
其中,Q为守恒矢量;E,F,G为3个坐标方向的对流通量;Ev,Fv,Gv为3个坐标方向的粘性通量.对流项采用一阶迎风格式,扩散项采用中心差分格式,压力和速度耦合采用SIMPLE算法.
湍流模型采用Spalart-Allmaras模型,通过对自由剪切流、高雷诺数时的近壁区流动、有限雷诺数时的近壁区流动、包含层流区与转捩的流动等4种状态的分析与建模,得到最终的方程[8]:
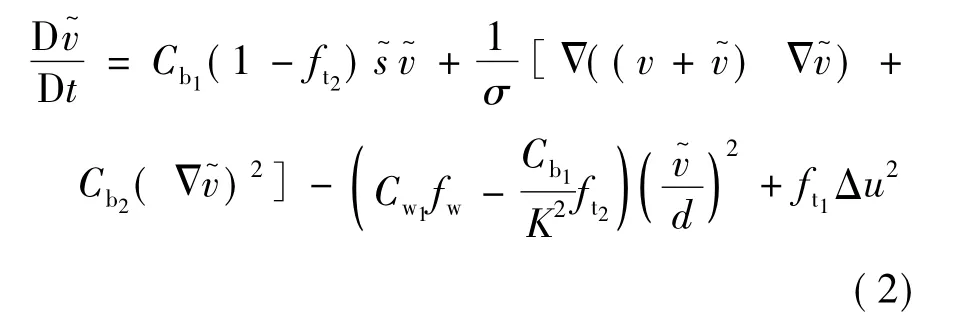
其中,封闭系数 Cb1=0.135 5,σ =2/3;Cb2=0.622;K=0.41;Cw1=Cb1/K2+(1+Cb2)σ.
流动区域为10×10×8倍旋翼直径,采用四面体网格对流场区域进行划分,用到的边界类型包括压力远场边界以及无滑移绝热固壁边界.
将本文计算方法所得结果与文献[6]中类似布局飞行器气动数据对比,见图2,可见旋翼处于不同方位角时,本文结果与文献数据较为吻合.
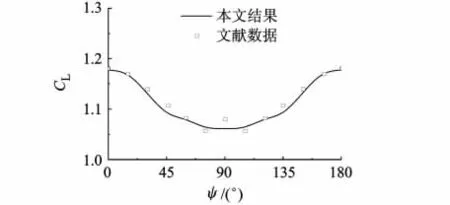
图2 全机升力系数C L随方位角ψ的变化
2 转换末段气动特性
2.1 气动力变化
旋翼转至不同方位角时,全机升力系数CL、阻力系数CD、侧力系数CC的变化规律如图3所示,气动力呈周期性变化.在1/2周期内(ψ=0°~90°),全机 CL单调下降,0°时 CL最大,90°时最小;CD总体呈上升趋势,方位角增大,CD增大;CC在45°时最大,0°与90°时为0.
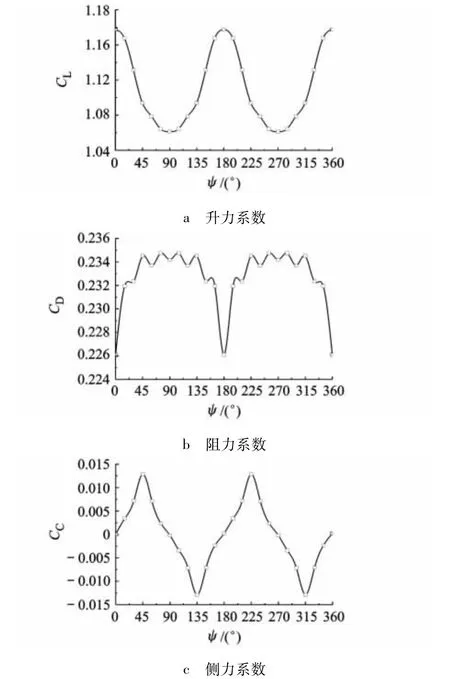
图3 全机气动力随方位角的变化
定义一个周期内气动力系数平均值:
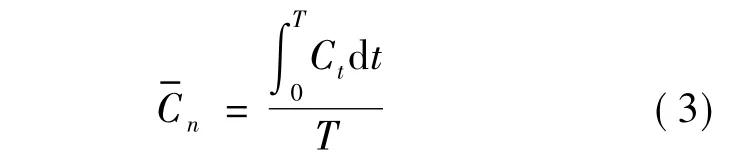
变化幅度:
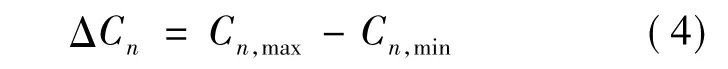
相对变化幅度:
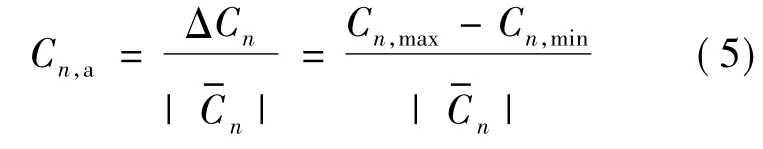
其中,Ct为 t时刻气动力系数瞬态值;Cn,max,Cn,min分别为一个周期内气动力系数的最大值与最小值;T为周期.
根据上述定义,可知在一个周期内,全机升力系数变化幅度为0.12,相对变化10.7%,阻力系数变化幅度0.0087,相对变化3.7%,侧力系数变化幅度0.026,如表2所示.
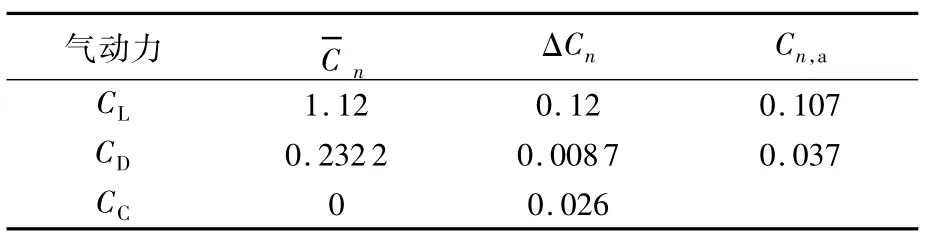
表2 气动力均值与幅值
全机升力系数变化主要由旋翼升力系数变化引起,如图4所示.在方位角0°~90°半周期内,旋翼升力系数变化具有3个特征:①左右旋翼均产生负升力;②左右旋翼升力系数均随方位角增大而减小;③相同时刻,右旋翼负升力绝对值大于左旋翼负升力绝对值.
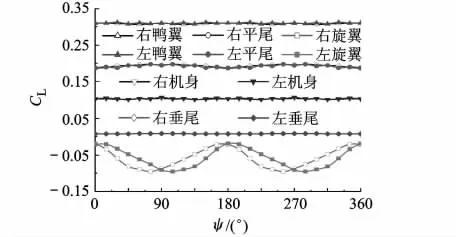
图4 部件升力系数随方位角的变化
旋翼采用对称椭圆翼型,总距为0时旋翼升力应为0,但在转换末段,旋翼实际产生周期性变化负升力,这一现象与原设想的旋翼完全卸载存在差别,与鸭翼、机身在旋翼旋转平面诱导的不均匀流场有关.
在旋翼旋转平面上,速度分布左右对称,前后不对称,见图5.旋转平面大部分处于下洗流场中,只在机身前部狭窄区域内存在上洗流场.
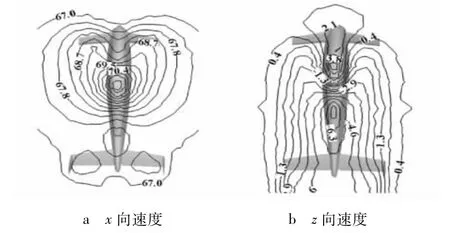
图5 旋翼旋转平面速度分布(无旋翼)
将旋翼升力系数表示为方位角为ψ的函数:
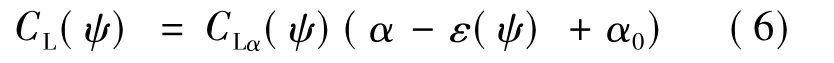
其中,α为来流迎角,转换末段α=0°;εψ为鸭翼、机身诱导的下洗角;α0为旋翼零升迎角,旋翼采用零弯度对称椭圆翼型,α0=0°.故可得
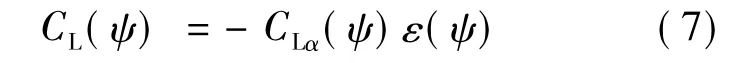
可见旋翼升力系数在不同方位角下均为负.
在1/2周期内,方位角增大,旋翼升力系数减小,原因为:①ψ=0°时,旋翼部分处于机身上洗流中,ψ增大,上洗逐渐变为下洗,且下洗角逐渐增大;②ψ由0°增至90°,相当于旋翼由斜掠翼变为平直翼,升力线斜率增大.由式(4)可得旋翼升力随ψ增大而减小.
旋翼处于前后不对称流场中导致左右旋翼升力系数不对称.在ψ=0°~90°范围内,左旋翼(后行)处于前部流场,受机身上洗影响,局部迎角与局部速度较大,升力较大;右旋翼(前行)处于后部流场,受机身对气流的阻滞与鸭翼下洗影响,升力较小.
旋翼在方位角由0°转到90°过程中,迎风面积增大,同时旋翼与机身干扰增大,全机阻力系数呈上升趋势.
侧力系数在ψ=0°~90°范围内先增大后减小,ψ=45°时最大.机身与垂尾是全机侧力变化的主要来源,见图6.机身侧力的变化主要由旋翼处于不同方位角时对机身的干扰不同引起,在ψ =0°与90°时,旋翼-机身组合体左右对称,侧力为0.ψ≠0°与90°时,旋翼-机身组合体左右不对称,机身产生不对称侧力.
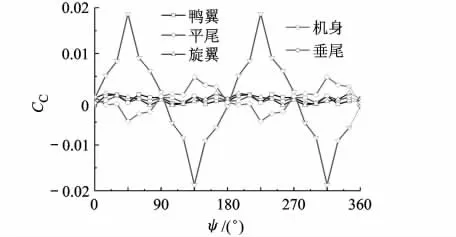
图6 部件侧力系数随方位角的变化
2.2 气动力矩变化
图7表示全机力矩系数随方位角变化,在1/2周期内,俯仰力矩系数单调减小,ψ=90°时为0,此时全机处于配平状态;滚转力矩系数与偏航力矩系数绝对值先增大后减小,在0°与90°位置时为0,45°位置左右达到峰值.
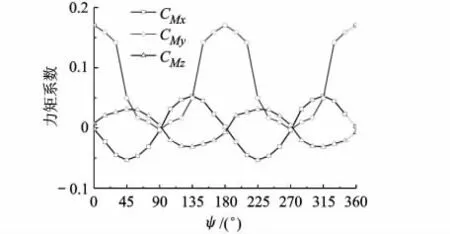
图7 全机力矩系数随方位角的变化
俯仰力矩系数的变化主要由旋翼与平尾引起.图8显示了ψ=0°时旋翼对称面压力分布,表现为:较大正升力-负升力-较小正升力,总体效果抬头力矩.ψ=90°时,旋翼压力中心对参考点的力臂长度较短,对全机俯仰力矩的贡献可忽略.因此旋翼从0°转到90°,抬头力矩逐渐减小直至0.
平尾俯仰力矩系数可表示为
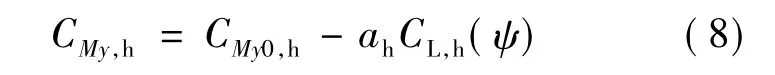
其中,CMy0,h为平尾零升力矩系数;CL,h(ψ)为平尾升力系数,是旋翼方位角的函数;ah为平尾力臂,由于力臂较长,故平尾升力系数产生微小变化可引起力矩系数较大变化.由图4可知,ψ=0°时平尾升力较小,产生低头力矩较小,ψ=90°时升力较大,产生低头力矩较大.
滚转力矩系数变化同样与旋翼升力系数分布及力臂变化有关.定义旋翼升力差为
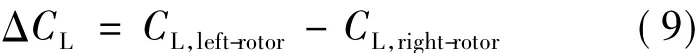
旋翼升力差随方位角的变化如图9所示,差值在ψ=45°时达到最大.由于左右旋翼力臂相等,因此右旋翼产生的负滚转力矩大于左旋翼产生的正滚转力矩,总滚转力矩为负.
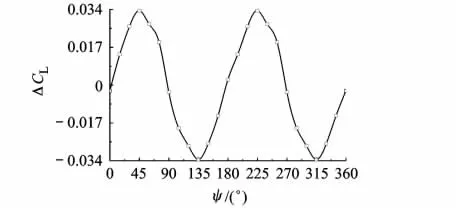
图9 左右旋翼升力差随方位角的变化
偏航力矩系数的变化与机身、垂尾侧力系数的变化有关.机身侧力在ψ=45°达到最大,且前半机身产生负侧力,后半机身产生正侧力,两者均产生正偏航力矩.垂尾侧力对全机偏航力矩的影响与机身相反.
2.3 焦点位置变化
转换末段旋翼处于不同方位角时,旋翼与全机焦点位置发生较大变化,全机焦点在ψ=0°时处于后限位置,ψ=90°时处于前限位置,见图10、图11.
全机焦点位置变化主要受旋翼、平尾焦点位置及升力线斜率影响,可用XfCLα表征翼面对焦点位置的拉动能力,XfCLα越大,对焦点后拉能力越强.图12表示ψ=0°~90°时旋翼、平尾对焦点的拉动能力变化.平尾流场受鸭翼、旋翼、机身流场影响,旋翼处于不同方位角时,对平尾的影响存在差别,从而使平尾升力线斜率产生微小变化.
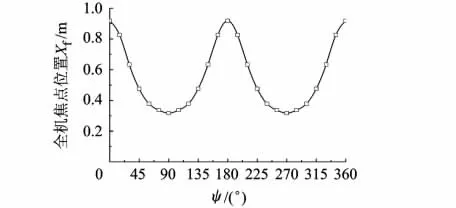
图10 全机焦点位置变化
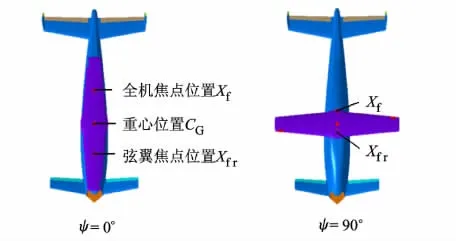
图11 ψ=0°与90°时旋翼与全机焦点位置
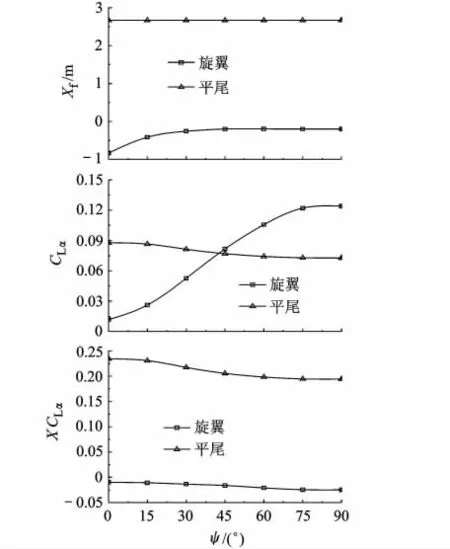
图12 旋翼、平尾焦点位置与升力线斜率变化
ψ=0°时,尽管旋翼焦点处于前限位置,但升力线斜率最低,故旋翼将全机焦点向前拉动作用仍最小.此时平尾升力线斜率最大,将全机焦点拉至最后.ψ=90°时,旋翼升力线斜率最大,将焦点向前拉动作用最强,平尾升力线斜率最小,将焦点向后拉动作用最弱,此时焦点处于前限位置.可见旋翼、平尾升力线斜率变化是全机焦点位置变化的主要原因.
3 结束语
1)鸭式旋翼/机翼飞行器转换过程末段,全机气动力及气动力矩随旋翼方位角均发生周期性变化,ψ=90°时(旋翼垂直于机体轴线)升力最小、阻力最大、抬头力矩最小,ψ=45°时侧力、滚转力矩、偏航力矩最大(小).其中升力系数变化幅度10.7%,阻力系数变化幅度3.7%.
2)旋翼处于鸭翼、机身诱导的前后不对称流场与旋翼转至不同方位角时对机身、尾翼的左右不对称干扰导致了全机气动力与气动力矩周期性变化.
3)转换过程末段,旋翼焦点位置变化、旋翼升力线斜率变化、平尾升力线斜率变化导致全机焦点位置变化幅度较大,移动量为0.6m,全机纵向静稳定性变化明显.
References)
[1] Mitchell CA,Vogel B J.The canard rotorwing(CRW)aircraft:a new way to fly[R].AIAA 2003-2517,2003
[2] Kim C,Lee J.Hub drag-reduction strategies of canard rotor/wing unmanned aerial vehicles[J].Journal of Aircraft,2007,44(4):1388-1391
[3] Lee JW,Jeon K S,Kim M,et al.Rotor design for the performance optimization of canard rotor/wing aircraft[J].Lecture Notes in Computer Science,2006,3984:932 -941
[4]曹旭,詹浩,邓阳平.尖部喷气驱动旋转机翼地面试验装置的研制[J].实验流体力学,2007,21(2):89 -92 Cao Xu,Zhan Hao,Deng Yangping.Developmentof experimental equipment for reaction driving rotor wing[J].Journal of Experiments in Fluid Mechanics,2007,21(2):89 -92(in Chinese)
[5]詹浩,邓阳平,高正红.椭圆翼型低速气动特性研究[J].航空计算技术,2008,38(3):25 -27 Zhan Hao,Deng Yangping,Gao Zhenghong.Investigation on aerodynamics performance of elliptic airfoil at low speed[J].Aeronautical Computing Technique,2008,38(3):25 - 27(in Chinese)
[6] Pandya SA,AftosmisM J.Computation of external aerodynamics for a canard rotor/wing aircraft[R].AIAA 2001-0997,2001
[7]陆志良.空气动力学[M].北京:北京航空航天大学出版社,2009:256-260 Lu Zhiliang.Aerodynamics[M].Beijing:Beijing University of Aeronautics and Astronautics Press,2009:256 - 260(in Chinese)
[8]朱自强,吴子牛,李津,等.应用计算流体力学[M].北京:北京航空航天出版社,1998:136-137 Zhu Ziqiang,Wu Ziniu,Li Jin,et al.Application of computational fluid dynamics[M].Beijing:Beijing University of Aeronautics and Astronautics Press,1998:136 -137(in Chinese)
(编 辑:李 晶)
Aerodynamic characteristic of canard rotor/wing aircraft in conversion
Li Yibo Ma Dongli
(School of Aeronautic Science and Engineering,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)
Niu Lingyu
(Beijing System Engineering Institute,Beijing 100101,China)
The aerodynamic characteristics and mechanism of canard rotor/wing(CRW)aircraft during conversion from rotary to fixed-wing flightwas numerically investigated.The variation of forces,moments and aerodynamic center with respect to rotor position are presented,the amplitude of lift,drag and aerodynamic center for this configuration in conversion can reach 10.7%,3.7%and 0.6m separately.The investigation shows that the cause of forces and moments variation is the asymmetry flow field in rotary plane and asymmetry interference between rotor and fuselage,the motion of aerodynamic center can be explained by the motion of rotor aerodynamic center and the variation of lift curve slope of rotor and horizontal tail.
canard rotor/wing(CRW)aircraft;aerodynamic characteristic;flow interference;flight mode conversion
V 275+.3
A
1001-5965(2011)03-0311-05
2010-07-14
武器装备预研重点基金资助项目(9140A25010208HK0101)
李毅波(1983-),男,湖南娄底人,博士生,liyibo1983@tom.com.
