考虑P－Δ效应的弹塑性反应谱归一化

蔡志恒，童根树

(浙江大学土木工程系，310058杭州，czh1984@139.com)

结构在遭遇达到设防烈度的地震作用下，能经受一定程度的塑性变形，对结构的安全并没有不利的影响.因此，现有的抗震规范，都允许结构在遭受本地区抗震设防烈度的地震影响时进入塑性阶段.但非线性分析较为复杂和耗时，此时，对简化的弹塑性地震力计算便出现了2种研究方向:间接法和直接法.间接法是通过对弹性地震力折减来获得弹塑性地震力;直接法是建立与弹性反应谱类似的弹塑性动力放大系数谱βμ谱，弹塑性地震力可以利用公式Fμ=kβμG直接获得，其中k为地震区域系数，G为结构质量.已有研究［1－5］表明:震中距和震级对强度折减系数R影响较小，而场地条件、阻尼比、滞回模型对R存在着不可忽视的影响.文献［6］首次用特征周期TgR对R谱进行归一化处理，很好地保留了R谱的峰值特性.文献［7－8］对特征周期作了进一步研究，分析了修正克拉夫模型和双折线模型的R谱.在大震作用下，结构的塑性变形将比弹性极限变形大好几倍，此时结构受重力二阶效应的影响将变得尤为明显，因此，折减系数R和弹塑性动力放大系数β都应考虑二阶效应的影响.文献［9］建议在设计中采用强度需求放大系数α=1/(1－μθ)，以考虑P－Δ效应的影响，并被1977年的墨西哥抗震规范采用;而我国的建筑工程抗震性态设计通则［10］给出的楼层剪力放大系数则为α= 1/(1－θ);二者存在巨大的差异.文献［11－12］的研究也认为应该考虑P－Δ效应的影响.由于2个特征周期Tga(弹性动力放大系谱峰值对应周期)和TgR(R谱峰值对应周期)并不一致，本文基于EPP滞回模型，进一步研究2个周期标准化的R谱和β谱，同时考虑二阶效应的影响.

1 分析方法

对单自由体系，由底部弯矩动力平衡得

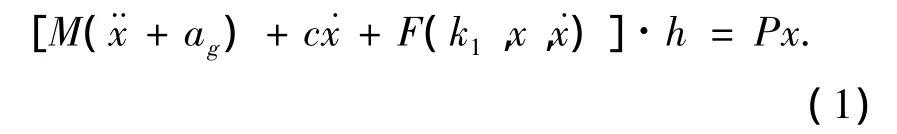
式(1)等价为

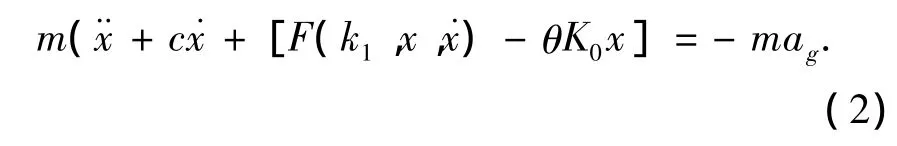
式中:m为系统质量;x为系统相对位移;F(kt，x，˙x)为结构恢复力;c为系统阻尼;kt为切线刚度; K0为初始弹性刚度;ag为地震加速度;θ为二阶效应系数，θ=P/hK0.

2 地震力折减系数

2.1 不考虑P－Δ效应的地震力折减系数

采用EPP滞回模型，各类场地条件下，ξ= 0.05时的R平均谱(即具有50%保证率的R谱)见图1(a)、1(b).横轴周期经过2个特征周期Tga与TgR的标准化后，很好地保留了R谱在Tga与TgR附近的峰值特性.而且，不同场地情况下的R谱形状与数值都比较接近，主要是由于横轴已经包含了与场地类别相关的特征周期.R变化规律也相仿:当T接近于0时，R都趋近于1;T＜Tga时，R基本随T线性增加;Tga＜T＜TgR时，R大致先降后升;Tga＜T＜2TgR时，R逐渐下降;当T＞2TgR时，R趋近于μ，满足等位移准则.

2.2 考虑P－Δ效应的地震力折减系数

二阶效应系数θ=0.05时的地震力调整系数平均谱见图1(c)、1(d)，考虑二阶效应系数后，对比图1(a)、1(b)可见:1)地震力调整系数下降.由于P－Δ效应，结构容易出现偏振现象，位移增大，意味着在相同调整系数情况下，延性需求增大，为了获得与不考虑二阶效应时相同的延性需求，必须减小调整系数，以减小位移;2)地震力调整系数依然在Tga与TgR处呈现峰值;3)整体的变化趋势有略微的改变，随周期延长和延性增大调整系数有增大现象.

3 动力失稳

图1 周期标准化的R谱

考虑P－Δ效应后，当折减系数过大时，结构容易发生动力失稳，其本质在于位移过大，因此定义如下动力失稳参数:Δmax1为不考虑二阶效应的弹塑性最大位移，μ1为延性开展系数;Δmax2为考虑二阶效应时的弹塑性最大位移，μ2为延性开展系数.当Δmax2≤Δmax1/(1－μ1θ)=Δlim时，结构的振动反应是稳定的;当Δlim＜Δmax2≤2Δlim时，结构的振动反应是半稳定的;当Δmax2＞2Δlim时，结构容易发生动力失稳，是不稳定的.

4 动力放大系数

4.1 不考虑P－Δ效应时的动力放大系数谱

图2为A类场地，θ=0、ξ=0.05时，不考虑P－Δ效应时的标准化的动力放大系数平均谱，可见，弹性状态(μ=1)时在Tga与TgR附近，较好地保留了峰值特性，尤其是Tga处，峰值最为明显，但随着延性系数μ的增加，峰值越来越不明显，也可以从这里解释折减系数谱中峰值特性的来源:结构保持弹性状态(μ=1)时，在2个特征周期处发生共振，反应剧烈，随着延性增加，塑性耗能增大，共振反应趋于平缓，延性越大，耗能越大，动力放大系数谱越平缓，而折减系数 Rμ=Fe/Fu= βe/βμ，此时就可以保留弹性谱的峰值特性，延性越大，峰值特性越明显.

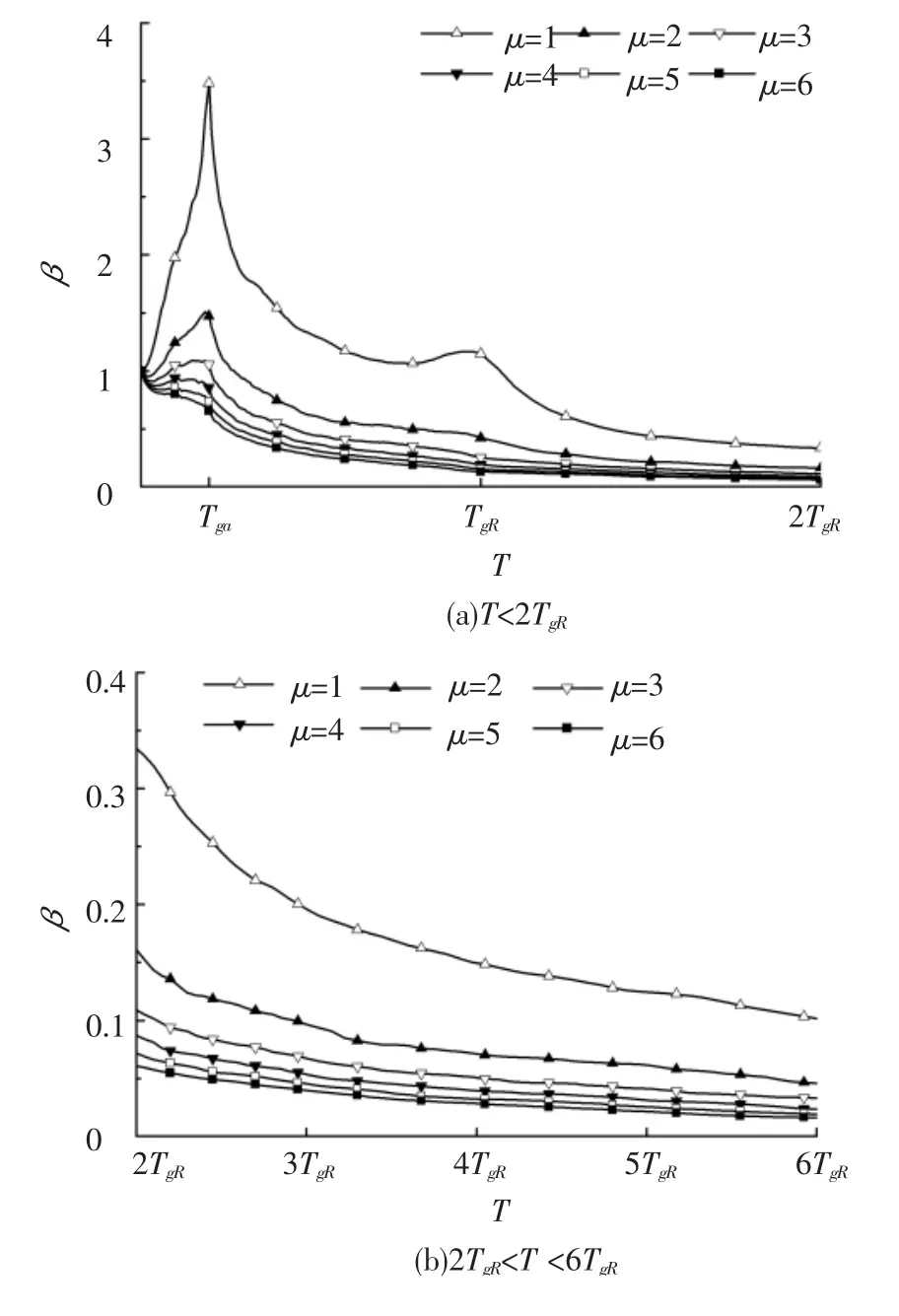
图2 周期标准化的β谱

4.2 考虑P－Δ效应时的动力放大系数谱

考虑P－Δ效应后的弹性动力放大系数平均谱见图3(a)、3(b)，二阶效应系数对其影响主要集中在T＜Tga时，二阶效应系数越大，动力放大系数β越大;而当T＞Tga后，二阶效应的影响开始变得不明显，尤其是当T＞TgR时，几乎没有差异.但从图3(c)、3(d)中可以发现，在延性系数μ=6时，无论是T＜Tga或是T＞Tga，动力反应平均谱受二阶效应的影响都非常明显，二阶效应系数越大，动力放大系数β也越大，这是由于允许结构发生塑性变形后，其位移增大，那么二阶效应的影响肯定增大.在弹性动力反应谱及μ=6的动力反应谱中，Tga附近的峰值特征都很明显，只是延性增大后，TgR处的峰值特性逐渐消失.

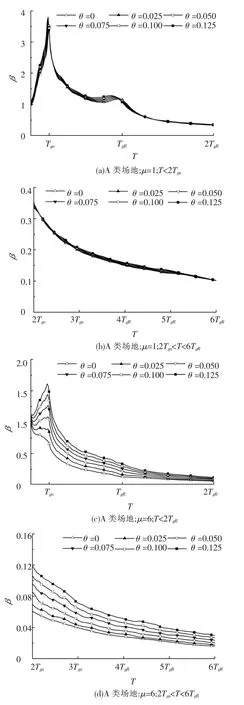
图3 不同二阶效应系数时的β谱

4.3 动力放大系数拟合谱

由以上分析可知，不同二阶效应系数及不同延性系数时的动力放大系数是不一样的，两者都对动力放大系数产生显著影响，拟合关系为

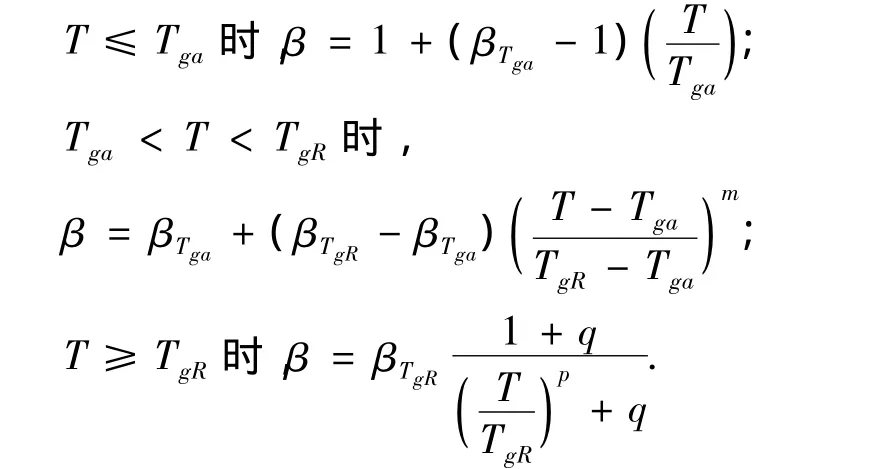
1)平均谱参数的取值.T=Tga时，βTga=1 +2μθ);T = T时，β=gRTgR1+3(μ－1)θ］;κa在A、B、C、D类场地分别为0.62、0.62、0.59、0.59;κR在A、B、C、D类场地分别为 0.575、0.505、0.605、0.725;p= 0.12μ+0.67，q=0.28μ－0.97－1.6(μ－1)θ(A类场地);p=0.10μ+1.15，q=0.26μ－0.76－(μ－1)θ(B、C、D类场地);m=0.3(TgRT)/(TgR－Tga)+0.2－0.1μ.

2)90%保证率谱的取值.T=Tga时，βTga=(1 +2μθ);T = T时，β=gRTgR+3(μ－1)θ］;κa在A、B、C、D类场地分别为0.52、0.52、0.52、0.485;κR在A、B、C、D类场地分别为 1.07、0.80、0.98、1.03;p = 0.10μ+0.38，q=0.20μ－1.00－(μ－1)θ(A类场地);p=0.16μ+0.74，q=0.60μ－1.20－2(μ－1)θ(B、C、D类场地);m =0.3(TgRT)/(TgR－Tga)+0.2－0.1μ.

4.4 阻尼比对动力放大系数的影响

为了反映阻尼比对动力放大系数的影响，本文引入参数η=βξ≠0.05/β，因此获得阻尼比ξ= 0.05的动力放大系数后，可以利用η对其调整来获得不同阻尼比时的动力放大系数.图4为不同场地类别、不同二阶效应系数、不同阻尼比时的η值，从图中可以得到:1)弹性状态下的η较塑性时大，此时在Tga与TgR处也呈现峰值;2)弹性状态时的η基本不受二阶效应系数影响，而塑性时的η随着二阶效应系数增大而增大;3)场地类别对η影响不大.

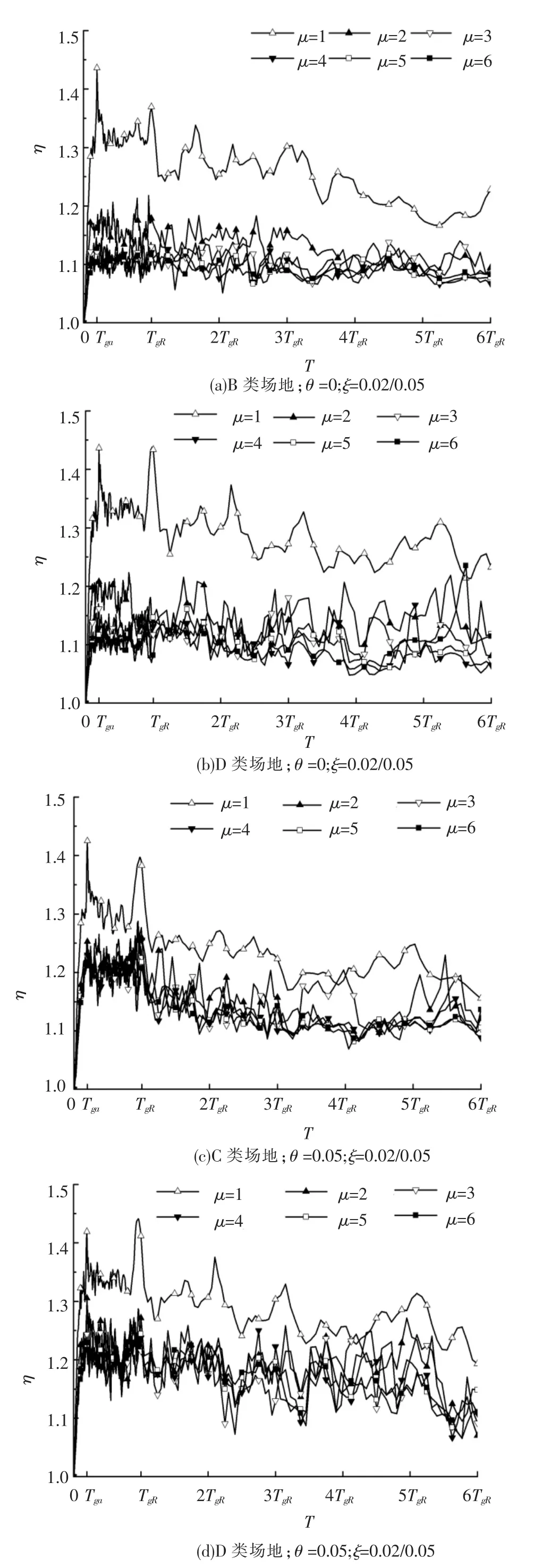
图4 不同条件的η谱

5 结论

1)对理想弹塑性(EPP)滞回模型的单自由度体系在4类场地，370条地震波下的地震响应进行分析，研究弹塑性地震力计算中所需的折减系数R和动力放大系数β，考虑了延性、阻尼比和二阶效应的影响.结果表明:周期用Tga与TgR标准化的R谱能很好地保留Tga与TgR附近的峰值特征;P－Δ效应对R影响非常明显，考虑P－Δ效应的R值要明显小于不考虑P－Δ效应的R值，在抗震设计中不容忽视.

2)提出了判断EPP弹塑性体系动力稳定、半稳定和动力不稳定的标准.用所建立弹塑性动力放大系数谱β谱来计算弹塑性地震力，要比采用R来对弹性地震力折减的结果更加理想.

3)给出了考虑二阶效应的50%保证率和90%保证率β谱的拟合公式.从公式可以看出，P－Δ效应大致使地震力增大到1+2μθ倍，近似于1/(1－2μθ).

4)阻尼比对β的影响，与场地类别关系不大.对βe谱的影响与二阶效应系数无关，随阻尼比增大，βe值减小;对βμ的影响与延性无关，随二阶效应系数增大，影响增强.阻尼比对βe的影响要大于对βμ的影响，但随着二阶系数的增大，对两者的影响趋近.

［1］ RIDDELL R，HIDALGO P，CRUZ E.Response modification factors for earthquake resistant design of short period structures［J］.Earthquake Spectra，1989，5 (3):571－590.

［2］VIDIC T，FAJFAR P.Consistent inelastic design spectra:streagth and displacement［J］.Earthquake Engineering and Structural Dynamics，1994，23:507－521.

［3］ LI H L，SANG W H.Determination of ductility factor considering different hysteretic models［J］.Earthquake Engineering and Sturctural Dynamics，1999，28:957－977.

［4］ BORZI B，ELNASHAI A S.Refined force reduction factors for seismic design［J］.Engineering Structures，2000，22:1244－1260.

［5］ CHOPRA A K，CHINTANAPAKDEE C.Inelastic deformation ratios for design and evaluation of structures: single-degree-of-freedom bilinear systems［J］.Journal of Structural Engineering，2004，130(9):1309－1319.

［6］ MIRANDA E.Site-dependent strength-reduction factors［J］.Journal of Structural Engineering，1993，119:3503－3519.

［7］ TONG G S，ZHAO Y F.Seismic force modification factors for modified-clough hysteretic models［J］.Engineering Structures，2007，29(11):3053－3070.

［8］ 赵永峰，童根树.双折线弹塑性滞回模型的结构影响系数［J］.工程力学，2008，25(1):61－70.

［9］ ROSENBLUTH E.Slenderness effects in building［J］.Journal of Structures Division，1965，91(1):229－252.

［10］ CECS160—2004.建筑工程抗震性态设计通则(试用)［S］.北京:中国计划出版社，2004.

［11］ TONG G S，ZHAO Y F.P－Δ effects on seismic force modification factors for modified-clough and EPP hysteretic models［J］.Advances in Structural Engineering，2009，12(4):579－593.

［12］ HAN S W，KWON O S，LEE L H.Investigationg of dynamics P－Δ effect on ductility factor［J］.Structural Engineering and Mechanics，2001，12(3):249－266.