土石坝动力离心模型试验颗粒流数值模拟

杨 贵，何敦明，刘汉龙，王年香

(1.河海大学岩土力学与堤坝工程教育部重点实验室，江苏南京 210098; 2.河海大学岩土工程科学研究所，江苏南京 210098; 3.江苏省交通运输厅航道局，江苏南京 210004;4.南京水利科学研究院岩土工程研究所，江苏南京 210024)

我国位于世界两大地震带(环太平洋地震带与欧亚地震带)之间，地震区域广阔而分散，地震频繁而强烈，主要发生在中西部及西南地区.“5.12”地震以后，大坝的抗震稳定性分析受到广泛关注.离心振动台模型试验是近年来迅速发展起来的一项高新技术，能够真实模拟原型应力场，反映土体在实际应力条件下的动力特性，被公认为研究岩土工程地震问题最为有效、最为先进的试验技术[1].目前该技术已在地震破坏机制、抗震设计计算、数值模型验证等方面显示出巨大的优越性，并取得良好的效果[2-5].

离心振动台由于模型箱尺寸较小很难进行较大尺寸模型的模拟.二维颗粒流程序PFC2D，属于离散单元法的一种，采用圆盘来模拟颗粒介质的运动及其相互作用，土体之间的相互作用通过颗粒之间的接触模型来表达，通过设定细观参数来实现材料的宏观力学性质，目前在岩土工程的多个领域都得到了广泛的应用[6-9].土石坝作为一种典型的散粒体材料集合体，可方便地采用该程序进行数值模拟，并能够获得坝体在地震荷载作用下的动力特性及坝体的破坏特征.本文以长河坝动力离心模型试验为基础进行数值模拟，主要研究水平向加速度作用下大坝的动力响应，同时开展各种影响因素对模型试验结果影响的数值模拟分析.

1 动力离心模型试验

振动台模型箱尺寸为700mm×200mm×42.5mm(长×宽×高)，模拟长河坝在地震荷载作用下坝体在坝顶加固和未加固情况下的动力特性和破坏模式.根据动力离心模型试验的相似理论，定义任一物理量 x的原型值与模型值之比为ηx，通过相似转换可得到离心模型振动台模型相似律[5].

模型试验模型比例 ηl=1400，试验过程中按平面问题进行考虑，试验布置如图1所示[5].离心机加速度40g，加载波形为正弦波，峰值加速度 9.52g，振动频率132.8Hz，振动历时0.75s.模拟长河坝在100 a超越概率2%地震条件下的动力响应.

图1 模型试验布置Fig.1 Layout of mode tests

长河坝筑坝材料共有10多种，在模型中要全部模拟很困难，根据试验目的，选择对影响坝体变形和稳定起决定作用的堆石料、覆盖层料和心墙料进行模拟.动力离心模型试验中堆石料最大粒径为10mm，心墙料最大粒径为2mm，覆盖层料最大粒径为2mm，模型密度比例ηρ=1.采用脆性胶将上下游坝坡面黏结，使坡面不再呈散粒状，而具有一定的黏结力，以模拟大块堆石料的咬合力.

2 细观数值模拟方法

动力离心模型试验在试验过程中按平面问题进行考虑，因此可以采用二维颗粒流程序PFC2D进行数值模拟分析.坝体的基本单元为圆盘单元，数值模拟主要步骤为:细观参数确定;坝体模型生成和地震荷载施加.

2.1 细观参数确定

数值模拟过程中颗粒之间接触模型的选择对试验结果有较大影响.与原型相比，模型试验和数值模拟过程中堆石料尺寸较小，颗粒之间的咬合力降低.模型试验过程中采用脆性胶将上下游坝坡面进行黏结，使坡面堆石料不再是散粒状，而具有一定的黏结力，达到模拟大块堆石的咬合力.数值模拟过程中采用线性接触模型进行材料模拟，通过设定颗粒之间的黏结强度(法向黏结强度bn和切向黏结强度bs)来实现较大颗粒之间的咬合力和心墙颗粒之间的黏结力.

数值模拟过程中若按材料原始级配进行模型生成，颗粒数目较多，计算效率较低，因此在建模过程中堆石料、心墙料和覆盖层料的最大和最小粒径均设为5mm和4mm，颗粒直径在最大和最小颗粒之间服从高斯分布，通过调整细观接触参数，使得数值模拟的材料与原试验材料力学性质基本一致[10].颗粒之间的细观接触参数如表1所示.

表1 颗粒流数值模拟参数Table 1 Parameters for simulation of PFC2D

2.2 土石坝模型生成

根据振动台模型坝的尺寸建立二维土石坝模型，坝高171mm，坝顶宽12mm，覆盖层厚度43mm.数值试样的生成过程一般是先建立模型框架，在其内部根据试验级配生成颗粒组，通过循环迭代消除模型内部的不平衡力.由于本次模拟的模型比较复杂，因此建模过程有所不同，通过颗粒产生时的“阴影”功能，采用分块建模的方式来完成，如图2所示.模型坝颗粒总数为4502.模型箱通过外围的墙体来进行模拟.

为监测坝体在地震荷载作用下的动力响应，在模型中通过设定8个监测点来测定坝体的动力响应，监测点的布置位置如图3所示.考虑到每个颗粒较小，且在运动过程中各种不确定性因素较多可能会影响试验的结果，模拟中采用测点附近的多个颗粒的动力响应平均值来描述该测点地动力响应.关于颗粒加速度的获得，采用PFC内置的FISH语言进行编程，根据牛顿第二定律进行求解.

图2 土石坝计算模型Fig.2 Model for earth-rockfill dams

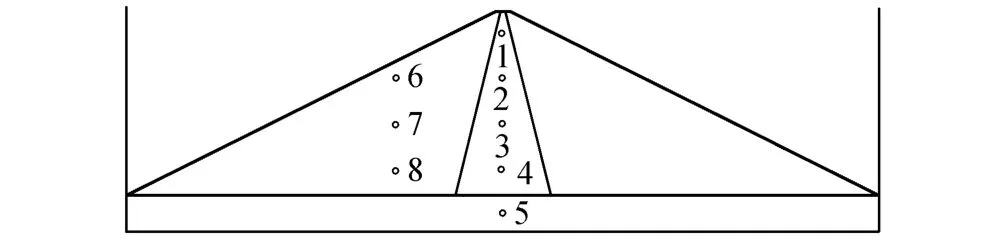
图3 坝体监测点分布Fig.3 Distribution of monitoring points in dam

2.3 地震荷载施加

二维颗粒流软件PFC2D可以方便地对墙体施加任意方向的位移和速度，而不能对墙体直接施加加速度，对于振动问题一般通过定义模型墙体沿指定方向随时间变化的速度来解决.鉴于此，需要对振动台输入的加速度时程进行转换，变成速度与时间的变化曲线，再通过内置的FISH语言施加到墙体上.图4为模拟过程中模型输入的加速度时程曲线和坝顶测点1处的加速度时程曲线.

图4 加速度曲线Fig.4 Curves of acceleration

3 模拟结果分析

3.1 坝体地震加速度反应

图5为坝体中心位置加速度放大系数与坝高的关系，相对坝高是指测点高程与坝基高程之差与坝体高度的比值，负值代表该点位于坝基之下，即覆盖层中.从图5可知，在相对坝高小于0.6时，加速度反应放大不明显，靠近坝体中上部，加速度反应增大较快，在坝顶附近最大.加速度分布规律与SL203—97《水工建筑物抗震设计规范》[11]规定的设计烈度为7度时，坝顶地震加速度放大系数相似.与动力离心模型试验结果相比其放大倍数有所降低，但分布规律保持不变.

图6为模型试验和数值模拟结果对应于图3中相同高程不同位置测点(2与6，3与7，4与8)加速度变化曲线.从图6可以看出，上游坝坡的加速度反应大于坝轴线处的坝体加速度反应，随着相对坝高的增大，两者之间的差值逐渐减小.数值模拟结果与模型试验结果在测点位置较高时，基本吻合，在测点位置较低时差异较大，模型试验结果小于数值模拟结果.这可能与数值模拟过程中测点8处存在悬浮颗粒有关，从而导致该处的加速度反应较大，比值偏大.

图5 加速度放大系数与坝高的关系Fig.5 Relationship between magnification coefficient of acceleration and dam height

图6 加速度反应Fig.6 Responses of acceleration

3.2 坝体地震位移

图7为坝体内测点(1，3和5)的水平位移和垂直位移时程曲线，水平位移正值代表向右，垂直位移负值代表向下.从图7可以看出，坝体在地震结束后存在残余变形，其变化规律与有限元计算结果基本一致.坝顶垂直沉降为1.04mm左右，根据动力离心模型试验的相似律反算到原型坝的垂直沉降约为145cm，与动力离心模型试验测得的结果反算到原型坝的变形161cm基本相当.

3.3 坝体地震破坏模式

图8为坝体上游坝坡不同部位检测颗粒在地震荷载作用下在空间的位置变化曲线，图8(a)中数字为颗粒的编号，图8(b)中的坐标以检测颗粒的初始位置为零点，向左和向下运动为负.从图8可以明确看出坝体在动力荷载作用下颗粒的运移过程:上游坝顶处的颗粒运动轨迹线角度小于坝坡倾角，表面颗粒是由坝坡内部向下运动，坝坡中心处的颗粒和坡角处颗粒的运动轨迹线倾角均大于坝坡倾角，表明颗粒是向坝体外部运动，即坝体的破坏模式为坍塌破坏.与动力离心模型试验结果和孔宪京等[12]的堆石坝振动台模型试验结果基本一致，图9为地震荷载结束后坝体轮廓，与真实的大坝在地震荷载作用下的破坏形态略有不同，坝体底部向两侧膨胀.这可能与模型试验过程中未考虑库水压力的作用和坝体填筑密度较高有关.

图7 坝体动位移Fig.7 Dynamic displacements of dam

图8 颗粒运移Fig.8 Transport of particles

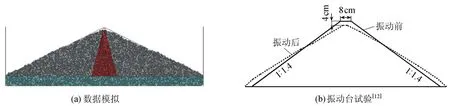
图9 坝体变形示意图Fig.9 Dam deformation

4 影响因素分析

根据前面的研究成果可以看出，数值模拟结果与模型试验结果基本一致.在此基础上充分利用数值模拟的优点，开展数值模型研究，分析堆石尺寸、峰值加速度、离心加速度和加速度方向变化对试验结果的影响.

4.1 堆石尺寸

堆石料尺寸较大时，颗粒之间的咬合力作用下降比较明显，材料表现出似黏聚力.图10为增设堆石颗粒之间黏结力(bn=bs=200Pa)，其他加载条件不变时坝体在地震结束后的示意图.从图10可以看出，当堆石料内部存在似黏聚力时，坝体的破坏模式仍为坍塌破坏，此时在坝体中上部出现局部颗粒的滑落、翻滚和滑坡.

4.2 峰值加速度

坝体的动力响应与输入的峰值加速度大小密切相关，开展不同峰值加速度输入情况下坝体的动力响应研究对研究坝体的动力变形特性有很大的作用.数值模拟过程中输入地震波波形为正弦波，荷载频率132.8 Hz，振动时间0.75s，加速度峰值分别为9.52g，11.40g和13.31g.

表2为坝体在不同加速度下的动力响应，从表2可以看出，随着输入加速度的增大，坝顶垂直位移逐渐增大，水平位移也逐渐增大，而坝顶加速度放大系数逐渐减小.模拟结果与动力离心模型结果基本一致，只是坝顶加速度放大系数较小.坝体的破坏模式保持不变，仍为坍塌破坏.

图10 考虑堆石尺寸后坝体变形示意图Fig.10 Damdeformation considering size of rockfill materials

表2 坝体动力响应Table 2 Dynamic responses of dam

4.3 离心加速度

离心振动台试验通过高速旋转增加模型的重力，使模型土体产生与原型土体相似的自重应力，此时模型的变形及破坏机制与原型相似，从而达到直接模拟复杂的岩土工程问题的目的.实际工程中受试验仪器本身条件的限制，很难达到预期的模型尺寸和所需的离心加速度，试验过程中会适当降低离心加速度.因此有必要开展不同离心加速度下离心模型试验研究，了解土体动力相应的变化规律.数值模拟输入波形为正弦波，主要参数见表3.

表4为不同离心加速度作用下数值模拟结果与模型试验结果.从表4可以看出，随着离心加速度的增大，坝体加速度放大系数减小;坝顶沉降逐渐较小.坝体的破坏模式基本保持不变.数值模拟结果与模型试验结果基本一致.

表3 数值模型试验主要参数Table 3 Main parameters for numerical simulation tests

表4 数值模拟与模型试验结果Table 4 Results of numerical simulations and model tests

4.4 加速度方向

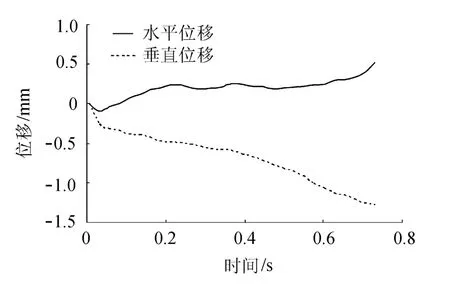
图11 坝顶位移曲线Fig.11 Curves for displacement of dam crest

实际的地震问题是一个复杂的三维问题，动力离心模型试验受仪器的限制目前只能进行单向的加速度输入.数值模拟可以方便地进行多向的地震加速度输入，根据前面的研究成果进行长河坝模型试验的双向地震输入研究，研究坝体的动力响应.输入地震波波形为正弦波，荷载频率132.8Hz，振动时间0.75s，水平向加速度峰值为9.52g，竖直向输入为水平向的2/3.

图11为坝体在水平向和垂直向动力荷载作用下的坝顶水平位移和垂直位移曲线.从图11可以看出，地震结束后坝顶沉降约为1.31mm，水平位移约为0.56mm.根据动力离心模型试验的相似律进行反算，则得到长河坝的坝顶沉降为184cm，水平位移为78 cm.与单向地震荷载输入相比，坝顶沉降增大，与有限元计算规律基本一致，表明采用颗粒流软件进行土石坝动力离心模型试验数值模拟研究是可行的，可用于分析复杂加载路径下的坝体动力特性.

5 结 论

a.二维颗粒流程序能够模拟土石坝动力离心模型试验，且规律基本一致.

b.在坝体同一高程处，坝坡处的动力响应大于心墙处.随着高程的增大，差值逐渐减小.

c.随着离心加速度的增大，坝顶沉降和加速度放大系数逐渐减小.

[1]章为民，赖忠中，徐光明.电液式土工离心机振动台的研制[J].水利水运工程学报，2002(1):63-66.(ZHANG Wei-min，LAI Zhong-zhong，XU Guang-ming.Development of an electrohydraulic shake table for the centrifuge[J].Hydro-Science and Engineering，2002(1):63-66.(in Chinese))

[2]ARULANANDAN K，ANANDRAJAH A，ABGHARI A.Centrifuge modeling of soil liquefaction susceptibility[J].Journal of Geotechnical Engineering，1983，109(3):281-300.

[3]章为民，日下部治.砂性地基地震反应离心模型试验研究[J].岩土工程学报，2001，23(1):28-31.(ZHANG Wei-min，KUSAKABE O.Dynamic centrifuge model test of sandy layer[J].Chinese Journal of Geotechnical Engineering，2001，23(1):28-31.(in Chinese))

[4]王年香，章为民.混凝土面板堆石坝动态离心模型试验研究[J].岩土工程学报，2003，25(4):504-507.(WANG Nian-xiang，ZHANG Wei-min.Dynamic centrifuge model test for concrete face rock fill dam[J].Chinese Journal of Geotechnical Engineering，2003，25(4):504-507.(in Chinese))

[5]王年香，章为民，顾行文，等.长河坝动力离心模型试验研究[J].水力发电，2009，35(5):67-70.(WANG Nian-xiang，ZHANG Wei-min，GU Xing-wen，et al.Dynamic centrifuge model test for Changhe dam[J].Water Power，2009，35(5):67-70.(in Chinese))

[6]杨贵，刘汉龙，陈育民，等.堆石料动力变形特性的尺寸效应研究[J].水力发电学报，2009，28(5):121-126.(YANG Gui，LIU Han-long，CHEN Yu-min，et al.Research on size effect of rock-fillmaterials ondynamic deformationproperty[J].Journalof Hydroelectric Engineering，2009，28(5):121-126.(in Chinese))

[7]周健，王家全，曾远，等.颗粒流强度折减法和重力增加法的边坡安全系数研究[J].岩土力学，2009，30(6):1549-1554. (ZHOU Jian，WANG Jia-quan，ZENG Yuan，et al.Slope safety factor by methods of particle flow code strength reduction and gravity increase[J].Rock and Soil Mechanics，2009，30(6):1549-1554.(in Chinese))

[8]CAI M，KAISER P K，MORIOKA H，et al.FLAC/PFC coupled numerical simulation of AE in large-scale underground excavations[J]. International Journal of Rock Mechanics and Mining Sciences，2007，44:550-564.

[9]BARDET J P，PROUBET J.Shear-band analysis in idealized granular material[J].Journal of Engineering Mechanics，ASCE，1992，118 (2):397-415.

[10]章为民.长河坝水电站砾石土心墙堆石坝筑坝料静动力试验报告[R].南京:南京水利科学研究院，2006.

[11]SL203—97 水工建筑物抗震设计规范[S].

[12]孔宪京，刘君，韩国城.面板堆石料模型动力破坏试验与数值仿真分析[J].岩土工程学报，2003，25(1):26-30.(KONG Xianjing，LIU Jun，HAN Guo-cheng.Dynamic failure test and numerical simulation of model concrete-faced rockfill dam[J].Chinese Journal of Geotechnical Engineering，2003，25(1):26-30.(in Chinese))