主成分分析在GPS高程拟合中的应用
2011-03-14岳东杰李立瑞郭培闪
岳东杰,李立瑞,郭培闪
(1.河海大学地球科学与工程学院,江苏南京 210098;2.中国电力工程顾问集团中南电力设计院,湖北武汉 430071)
GPS测量以精度高、速度快、操作简单等诸多优点在各行各业得到广泛的应用.由于GPS测量直接得到的高程为相对于WGS-84椭球的大地高,而实际应用的高程为相对于大地水准面的正常高,为此必须进行高程转换.通常采用一定的数学模型对测区的高程异常进行拟合,进而结合GPS测量的成果,求出待测点的正常高[1].在各种拟合法中,多项式拟合法以其计算简单、易于编程实现而得到广泛应用.即在小区域内,将似大地水准面看成曲面或平面,将高程异常ξ表示为平面坐标(x,y)(或大地坐标(B,L))的多项式函数f(x,y),通过区域内的已知控制点(大地高和正常高均为已知),构造误差方程,采用最小二乘法确定模型中的参数,从而确定测区的似大地水准面形状,求出其余各点的高程异常.其数学模型为

式中:f(x,y)——以平面坐标表示的似大地水准面函数;ε——拟合误差;ξ——高程异常.f(x,y)的多项式形式为
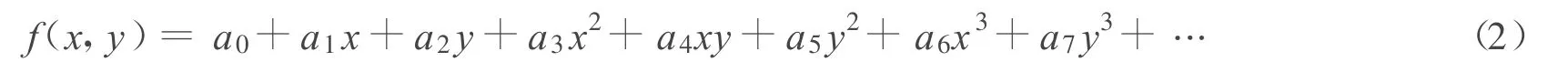
对于n个已知点,写成误差方程的形式为


上述模型在实际应用中存在多项式阶数(拟合参数个数)的确定问题,以往是根据经验确定.实践验证表明并不是阶数越高、参数越多越好;其次,当拟合参数过多时,系数之间会产生很大的相关性,导致法方程系数病态,最小二乘解不稳定.针对以上问题,本文尝试采用主成分分析法,根据携带信息的多少逐步选取独立的主成分进行回归计算,克服参数相关性的影响,提高计算结果的稳定性.
1 主成分分析法原理及其计算步骤
主成分分析最早是由美国统计学家皮尔逊在1901年的生物学理论研究中引入的,它从多指标分析出发,运用统计分析原理与方法提取少数几个彼此不相关的综合性指标而保持其原指标所提供的大量信息的一种统计方法,也是考察多个变量间相关性的一种多元统计方法,研究如何通过原来变量的少数几个线性组合来解释原来变量绝大多数的信息.具体地说,就是将高维空间的问题转化到低维空间去处理,使问题变得比较简单、直观,而且这些较少的综合指标之间互不相关,又能提供原有指标的绝大部分信息.目前主成分分析方法已经广泛地应用于图像识别、图像分析、管理决策、回归分析、模式识别、时间序列预测等各个领域[2-6].
设X=(x1,x2,…,xp)是p维随机向量,E(X)=μ,Cov(X)=Q.主成分分析的思想就是将这p维向量(x1,x2,…,xp)综合成尽可能少的q维综合向量F=(f1,f2,…,fq)(q<p),而且要求这些新的综合向量(f1,f2,…,fq)既能充分反映原来p维向量(x1,x2,…,xp)所反映的信息,又互不相关[7-8].
考虑到fi=t1ix1+t2ix2+t3ix3+…+tpixp(i=1,2,…,p),记为矩阵形式fi=Xti,其中ti=(t1i,t2i,t3i,…,tpi)T,‖ti‖=1.
要使f1携带最多的信息,即要求f1的方差达到最大值.f1的方差可为

式中:N——X的样本数;Q——X的协方差阵.而当X中的变量均是标准化后变量时,Q就是X的相关系数矩阵.

对φ求关于t1和λ1的偏导,并令其为零,有

由式(6)得

由此可见,t1是Q的一个标准化特征向量,它对应的特征值为 λ1.由所以t1对应的特征值 λ1应取到最大值,t1为最大特征值对应的特征向量,这里称 λ1为第一主轴,f1=X为第一主成分[9-10].
依次可以推出其他主轴及其对应的主成分f2,f3,…,fq:

对主成分进行线性拟合回归,回归方程为
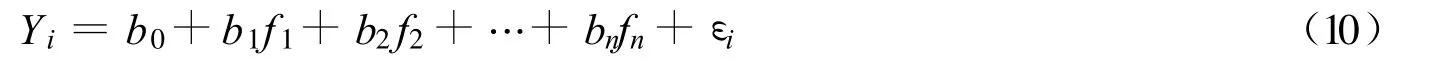
满足

利用最小二乘法求出系数.通常根据一定的累计贡献率(如90%)来决定回归因子的个数n.
归纳起来主成分分析的计算步骤如下:
a.为了防止数值差别过大和量纲不同影响方程组的求解,对数据进行标准化处理

b.计算标准化后矩阵X*的协方差阵Q(Q也是X的相关系数阵).
c.求Q的特征值λ1>λ2>…>λq及其对应的特征向量;计算所有的主成分
d.对f1,f2,…,fq进行线性拟合回归,得到主成分分析回归方程y=b0+b1f1+b2f2+…+bqfq;
e.将式(9)代入主成分分析回归方程,得到用原始自变量因子表示的方程
2 实例计算分析
为了验证主成分分析在GPS高程拟合上的适用性,选取苏通大桥首级施工控制网中的16个控制点(A1~A13为位于江堤上的点,S1~S3为位于江中间的点)进行计算分析.为了避免由于拟合点的选取对检验结果的影响,各种计算方案均选择相同的11个均匀分布的控制点作为拟合点,位于拟合点区域内的5个点作为检核点.图1为苏通大桥区域高程异常等高线图.可见该区域高程异常面相对平缓,略有起伏[11].
根据检核点高程异常的已知值ξi与拟合值ξ′i之差Δξi,计算拟合的外符合精度,其中n为检核点个数.
首先对数据进行多项式拟合,分别选取式(2)中3个、4个、6个、8个参数进行拟合计算,计算结果列于表1.各检核点的已知值与拟合值之差以及外符合精度见表2.

图1 苏通大桥区域高程异常等高线(单位:m)Fig.1 Contour map of height anomaly of Su-Tong Bridge area(unit:m)

表1 2种方法计算的参数比较Table 1 Comparison of parameters between two kinds of methods
从表2可见,若直接采用多项式拟合,采用3参数、4参数结果相对较好,随着参数个数的增加,或者幂次的增加,精度越来越低.这是由于参数个数的增加,后面因子与前面各因子只是简单平方、立方关系,从而导致系数矩阵存在较大的相关性,影响拟合结果.
对数据进行主成分分析,在不同的参数个数下(取累计贡献率满足99%的前几个因子),计算出的参数列于表1,各检核点的已知值与拟合值之差以及外符合精度见表3.

表3 不同参数下主成分分析拟合结果与已知结果比较Table 3 Comparison between fitting results by principal component analysis and given ones under different parameters mm
从表1可见,相同参数个数时,两种方法拟合系数有很大不同,这是由于主成分分析顾及了因子之间的相关性.
表3与表2比较可见,主成分分析较好地改善了因子之间相关性对结果的影响,具有较好的抗相关性能力,而且从拟合精度方面均有较大提高.3参数、4参数法二者结果一致,说明采用平面与双线性曲面拟合模型不足于描述该区域大地水准面的形状,这与图1显示的结果一致.
从以上计算结果可以得出以下结论:(a)多项式拟合法的精度受参数个数影响较大,但并不是参数越多,精度越高.随着参数的增多,参数的相关性增强,多余观测数目相应减少,导致拟合精度降低,而且当因子次数过大时,还会使模型出现一些峰值,对真实情况造成扭曲.(b)主成分分析法受参数个数影响较小,因为主成分分析法本身能够很好地处理数据的相关性,降低数据的相关度.(c)在算例分析的过程中,主成分个数的选取是按99%的累计贡献率来取舍的,计算过程中,一般取3个主成分分量就能满足要求,有效地降低了数据的维数.(d)主成分分析法虽然受参数选取多少的影响较小,但选取参数过多过少都不合适,参数个数过少会导致模型对真实世界的反应程度不够,参数个数过少又会使计算量急剧增加.在对算例进行计算试验过程中发现,选择4~7个参数或者二次多项式时较好,建立的模型精度较高而且计算量又不大.
3 结 语
在进行多项式拟合时,多项式的阶数或参数个数的选取直接影响拟合的结果与精度,参数过少或阶数过低,尽管可以避免参数相关,但可能不足以反映实际情况;参数过多又容易受到数据相关性的影响,造成结果不稳定.主成分分析根据携带信息的多少逐步选取主成分,可以规避数据相关性的影响,因此受参数个数影响小,计算结果稳定,而且能有效降低数据冗余度,是一种比较好的拟合方法.
[1]岳东杰,黄腾.GPS高程的抗差拟合推估[J].河海大学学报:自然科学版,1999,27(6):90-93.(YUE Dong-jie,HUANG Teng. Anti-error fitting of GPS height[J].Journal of Hohai University:Natural Sciences,1999,27(6):90-93.(in Chinese))
[2]李红祥.偏最小二乘回归及其在大坝安全监控中的应用[D].南京:河海大学,2009.
[3]张鹏.多指标综合评价理论与方法问题研究[D].厦门:厦门大学,2000.
[4]李磊,金菊良,梁忠民.核主成分分析的参数优化及其在水资源可持续利用综合评价中的应用[J].水利水电科技进展,2009,29(4):36-38.(LI Lei,JIN Ju-liang,LIANG Zhong-min.Parameters optimization of kernel principal component analysis and its application in evaluation of water resources sustainable utilization[J].Advances in Science and Technology of Water Resources,2009,29 (4):36-38.(in Chinese))
[5]余祖德,周明友,陈俊芳.基于模糊主成分分析法的供应商评价与选择决策[J].重庆交通学院学报,2006,25(3):111-115. (YU Zu-de,ZHOU Ming-you,CHEN Jun-fang.Appraisement and selection decision of suppliers based on the method of fuzzy principal component analysis[J].Journal of Chongqing Jiaotong University,2006,25(3):111-115.(in Chinese))
[6]胡平香,张鹰,王进华,基于主成分融合的盐田水体遥感分类研究[J].河海大学学报:自然科学版,2004,32(5):519-522. (HU Ping-xiang,ZHANG Ying,WANG Jin-hua.Principal component fusion-based classification of salt field water bodies with remote sensing technique[J].Journal of Hohai University:Natural Sciences,2004,32(5):519-522.(in Chinese))
[7]何秀丽.多元线性模型与岭回归分析[D].武汉:华中科技大学,2005.
[8]何晓群.现代统计分析方法与应用[M].北京:中国人民大学出版社,2007:281-315.
[9]李艳军.多元线性模型回归系数的主成分估计[D].长春:东北师范大学,2006.
[10]曾鹏,王绍棣.多变量时间序列的主成分分析及估计[J].南京邮电学院学报,1996,16(4):112-116.(ZENG Peng,WANG Shao-di.The main component analysis and estimation of multi variable time series[J].Journal of Nanjing Institute of Posts and Telecommunications,1996,16(4):112-116.(in Chinese))
[11]邬昱昆,岳东杰,杨柏宁.GPS水准在苏通大桥工程建设中的应用研究[J].测绘通报,2007(2):58-60.(WU Yu-kun,YUE Dong-jie,YANG Bai-ning.On the application of GPS leveling in the Sutong Bridge[J].Bulletin of Surveying andMapping,2007(2):58-60.(in Chinese))
