磁流变液微观结构的数值模拟

李杰如，杜成斌

(1.河海大学文天学院，安徽马鞍山 243031;2.河海大学力学与材料学院，江苏南京 210098)

磁流变液是一种非常具有发展前途和工程应用价值的新兴智能材料，被认为是最具前途的智能材料之一[1].磁流变液是由非胶体的细小颗粒分散溶于绝缘基液中形成的悬浮液，在外磁场作用下能产生明显的磁流变效应，其力学、热学、流变学性能等会迅速发生变化，响应时间很短，为毫秒量级，且这种液态和固态之间快速转化是可逆的.在该转化过程中，磁流变液的黏度保持连续、无级变化，固化强弱可由外加磁场控制，能耗极小，可实现实时的主动控制[2-5].

1948年Rabinow[6]最早发明了磁流变液及其应用装置离合器.Ginder等[7]认为在外磁场作用下，磁流变液中的铁磁性固体颗粒形成的是一条一条的单链，并从磁性固体颗粒的非线性磁化、磁饱和以及相邻颗粒接触位置处的局部磁场等方面进行了有限元计算，得出了磁流变液的剪切屈服应力的极值与磁性固体颗粒的饱和磁化强度成正比的结论，该结论也被后来的实验所证实.Rosensweig[8]设计出一种平均场模型——层模型，由于该模型忽略了相邻颗粒间的磁场集中效应，其结果与实验值相比往往偏低.Bossis等[9-10]将Klingenberg等[11]利用电流变液推导出的恢复力公式应用于磁流变液，但由于没有考虑磁性粒子的非线性磁化过程，其结果往往偏大.

近年来，国内武汉理工大学的阮中尉[12]建立了BCT结构(体心四方结构)模型和物理材料模型，得到了磁流变液受小角度剪切变形情况下其剪切应力的理论计算公式;中国矿业大学的赵四海等[13]研究了磁流变液中颗粒的相互作用，分析了磁流变液产生链状结构的原因，推导出磁流变液在外磁场作用下的屈服应力公式;广东工业大学陈伟俊[14]在对各种磁流变液的力学模型对比分析的基础上，根据磁场的库仑定律，提出了一种能够简洁表示各种因素对磁流变液力学性能影响的力学模型.

基于微结构的建模及力学分析只能描述磁流变液的宏观特性，不能描述微结构的形成机制及其演化过程.影响磁流变液性能的因素很多，单纯从实验或宏观角度很难系统分析各因素的影响及效果，而基于微观角度的数值模拟方法可以有效弥补这些缺陷，有利于优化磁流变材料的性能，设计高性能磁流变液.本文从数值模拟角度出发，利用分子动力学中的速度Verlet算法，基于磁流变液中磁性颗粒的实际受力，建立磁流变液链化和剪切的分析模型，采用Matlab语言编程，分析粒子的运动规律，探讨磁流变液微观结构的链化形成过程和剪切变形过程.

1 磁性颗粒的力学模型

在外加磁场的作用下，颗粒被磁化成偶极子在基液中产生运动，粒子在运动过程中起重要作用的力是颗粒之间的磁力、排斥力和基液对颗粒的黏性阻力.其他力由于影响很小，可以忽略不计.

1.1 磁性颗粒受力分析

1.1.1 颗粒之间的磁力

假设磁流变液中的基液是不可磁化的，其中的铁磁性固体颗粒为大小相同的圆球状，粒子的半径均为R，体积为V，在外加磁场H作用下，把固体颗粒看成是一个个磁偶极子，其方向与外加磁场方向相同.则颗粒被磁化后的磁矩[15]为

式中:M——磁化强度，M=χ H;χ——颗粒的磁化率.

颗粒i受到的磁力表达式[16]为

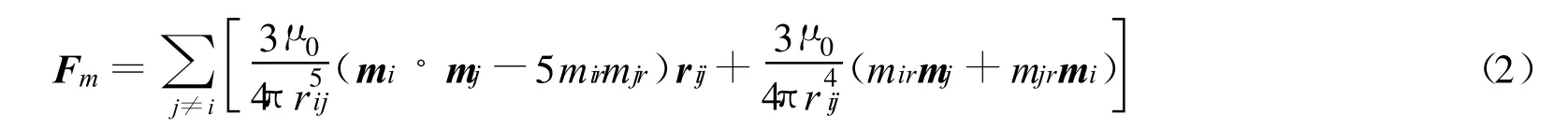
式中:μ0——真空磁导率;rij——两颗粒i和j之间的相对位置矢量(指向i)，rij=‖rij‖;mir，mjr——磁矩mi和mj沿相对位置矢量rij方向的分量大小.

假设磁场方向为竖直向上，两颗粒i和j之间的中心连线与磁场的夹角为θij，利用式(1)，式(2)所示的磁力表达式可改写为

1.1.2 颗粒之间的排斥力

颗粒在运动过程中由于发生碰撞而相互排斥，排斥力[17]为

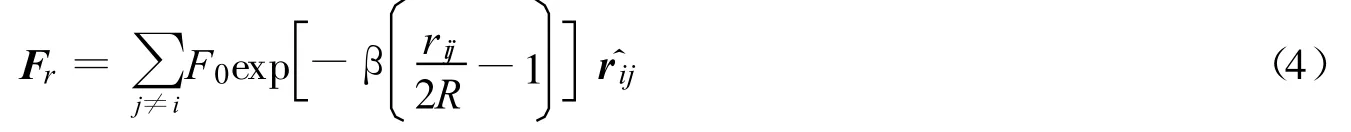
式中β为材料参数.

由式(3)可以看出，当粒子沿磁场方向排列且接触时，颗粒之间的磁力最大.F0可以取为两个颗粒相接触时的最大磁力，此时粒子沿磁场方向排列且接触，rij=2R，Fm=-Fr，F0的取值为

1.1.3 基液对颗粒的黏性阻力

假设颗粒为半径为R的圆球形，基液为黏性不可压流体，速度不太大时颗粒在静止液体中平动时受到的阻力Fv由Stokes阻力公式[18]来表示:

式中:η——液体的黏性系数;r——颗粒的位置矢量;v——颗粒运动的速度矢量.

1.2 颗粒运动的动力学方程

设单个颗粒质量为m，则

式中ρ为铁磁性固体颗粒材料的密度.

由牛顿第二定律，颗粒运动的动力学方程为

1.3 颗粒运动的模拟迭代算法

无外加磁场时颗粒在基液中随机分布，受到磁场作用后，颗粒即被磁化成一个个的磁偶极子，受到其他颗粒对它的磁力和排斥力等力的作用，从而具有了加速度，这样速度的增量和位移的增量就可以求出.而颗粒的位置在位移增量的影响下就发生了改变，从而颗粒受力也发生了改变，引起加速度和速度的改变.依次求出每个时间步长内的加速度、速度和位移，直到系统达到稳定即平衡状态为止.

分子动力学中，常见的求解运动方程的算法有Verlet算法、Leapfrog(蛙跳)算法、Gera(预测-校正)算法和Velocity Verlet算法(速度Verlet算法)等.速度Verlet算法可以同时给出位置、速度和加速度，并且不损失精度，所以本文的模拟过程选择速度Verlet算法.该算法需储存每个时间步颗粒的坐标、速度和力，每步计算涉及2个时间步，需要计算颗粒的位置更新以后和速度更新之前的力[19].

由于无外加磁场时，颗粒是随机分布在基液中且几乎静止不动，所以颗粒的初始位置由随机函数产生，初始速度为零，则t时刻的颗粒运动的加速度为

设模拟时所用的时间步长为Δt，则t+Δt时刻的颗粒位置为

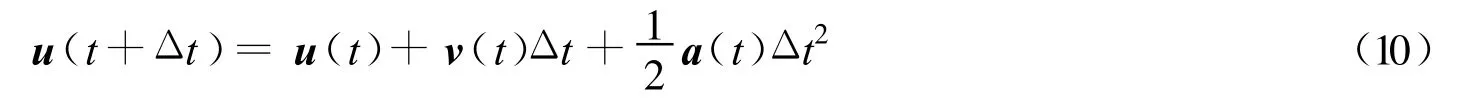
t+Δt时刻的颗粒速度为

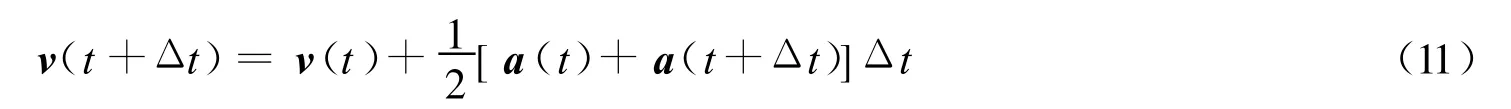
颗粒的位置、速度和受力不断更新，式(9)，(10)和(11)不断循环，直至颗粒的位置达到稳定状态(稳定判据为系统动能小于设定值)，即认为循环终止.模拟区域采用周期性边界条件.

2 模拟结果分析

2.1 链化过程的模拟

模拟中颗粒磁化率 χ=1，真空磁导率 μ0=4π×10-7H/m，材料参数 β=9，固体颗粒材料的密度ρ=7.5t/m3，基液的黏性系数η=0.001Pa◦s，外加磁场强度H=10.7kA/m.为了得到最好的链化效果，取颗粒体积百分率ξ=30%，颗粒半径R=5μ m，步长20μ s.链化过程模拟结果见图1.颗粒链化过程先快后慢，整个链化过程所耗费的时间在2～3ms之间.

图1 颗粒链化过程Fig.1 Illustration of chain process for particles

颗粒的体积百分率对磁流变液的性能有很大的影响，一般要在15%～30%范围内.下面以R=5 μ m为例，适当扩大模拟范围来比较不同颗粒体积百分率时颗粒成链的区别.图2为颗粒体积百分率ξ=15%，20%，25%和30%时的模拟结果.

图2 不同颗粒体积百分率的模拟结果Fig.2 Simulated results of different volume percentages for particles

从图2可以看出，颗粒体积百分率较小时，所形成的通链较少，甚至几乎没有，达到稳定状态时，大多数粒子还是以支链、孤链或单个粒子的形态存在.随着颗粒体积百分率的增加，通链逐渐增多，支链、孤链和单个的粒子在减少.颗粒体积百分率越大，所成通链越多.所以，在条件容许的范围内，在充分考虑粒子沉降性的基础上，应尽可能地增大颗粒的体积百分率.

2.2 剪切过程的模拟

磁流变液在受到外界的作用发生剪切流动时，基液也会同时流动.设其沿x正方向流动，剪切速率为﹒γ，则颗粒所受黏性阻力公式(6)应改写为

以图2(d)的模拟结果作为初始条件，上板在外力作用下作匀速剪切运动，剪切速率为﹒γ=200s-1，下板固定不动，其微观结构的演变过程如图3所示.

图3 低剪切速率下的剪切过程模拟Fig.3 Shear process at low shear velocity

由图3可以看出链逐渐向剪切方向倾斜，部分链发生断裂，同时生成新链，新链由断链、支链和孤链等重组生成，但是支链、孤链和单个粒子几乎始终存在.旧链的断裂和新链的生成基本上达到动态平衡的状态，也就是说，宏观上，磁流变液的剪切应力基本上应该是稳定的.

仍然以图2(d)的模拟结果作为初始条件，剪切速率为﹒γ=600s-1，其微观结构的演变过程如图4所示.

图4 高剪切速率下的剪切过程模拟Fig.4 Shear process at high shear velocity

图4结果表明，高剪切速率下，粒子向剪切方向的倾斜程度变大，但是通链减少，新链的生成速度明显跟不上旧链的断裂速度，在宏观上应表现为高剪切速率下，随着剪切速率的增加，磁流变液的剪切应力下降.

2.3 剪切应力的计算

根据磁力的计算公式，当颗粒沿磁场方向排列时，底板所受磁力在垂直于磁场的方向，即 x方向上分量为零.当颗粒受到外界的剪切作用而倾斜时，磁力在x方向上就有了分量，颗粒对底板在水平方向上的力的分量大小，宏观表现为剪切应力的大小.

设不受剪切时同一链中相距k个颗粒的2个颗粒之间的距离为 dk=2kR，则剪切过程中，链被拉长后，该距离变为dk=2kR/cosθ，则单链对宏观剪切应力的贡献，即单链的剪切强度为

单位面积内的链条数为

式中:S——磁流变液的底面积;L——磁流变液的高度.

单位横截面面积内各链对宏观剪切应力贡献的和为

因为磁流变液中的磁链并不都是通链，所以要乘以一个折减系数 φ.

磁流变液的宏观剪切应力为无铁磁性颗粒时基液的剪切应力τ0加上铁磁性颗粒对剪切应力的贡献¯τ，即

利用式(13)计算的单链的应力-应变曲线见图5;根据式(16)计算出的磁流变液的应力-应变曲线见图6;不同磁感应强度的应力-应变曲线见图7;不同颗粒体积百分率剪切应力变化情况见图8.

图5 单链的应力-应变曲线Fig.5 Stress-strain curve of single chain

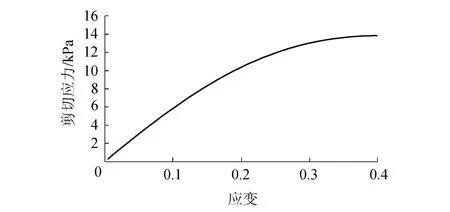
图6 磁流变液的应力-应变曲线Fig.6 Stress-strain curve of MFR

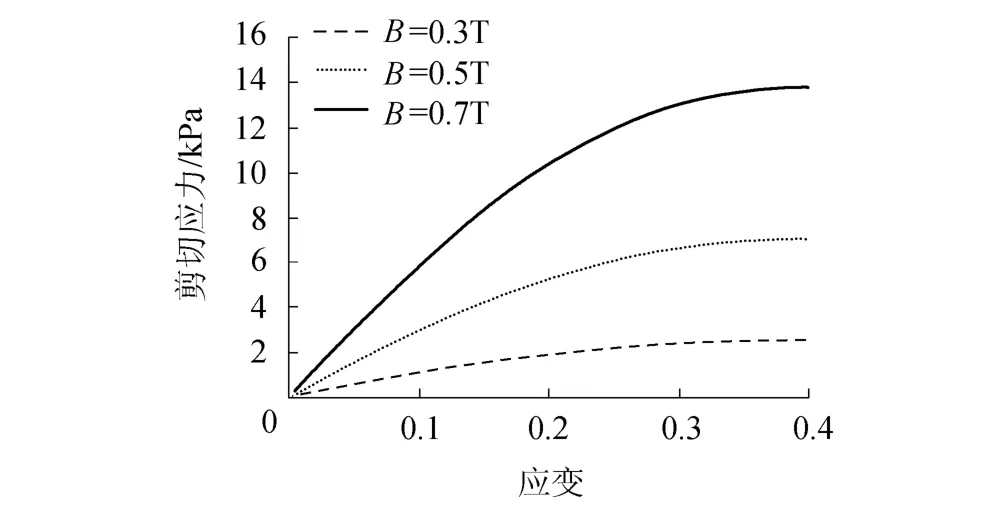
图7 不同磁感应强度的应力-应变曲线Fig.7 Stress-strain curves under different magnetic induction intensities

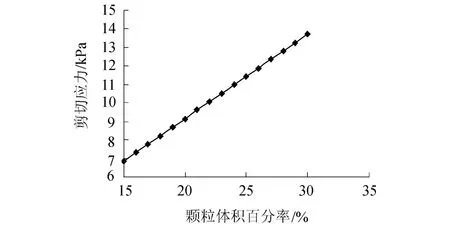
图8 不同颗粒体积百分率的剪切应力变化Fig.8 Variation of shear stress under different volume percentages of particles

从图5、图6可以看出，不同于单链的剪切强度先增大后减小，磁流变液的剪切强度只增大不减小.从图7可以看出，随着磁感应强度的增大，磁流变液的剪切应力有着显著提高.从图8可以看出，随着颗粒体积百分率的增大，磁流变液的剪切应力几乎呈线性增加.

3 结 论

a.颗粒链化的变化过程先快后慢，在1ms之内就可以形成链化，然后慢慢调整位置，最终趋于稳定，整个链化过程所耗费的时间在2～3ms之间.

b.不同颗粒体积百分率的磁流变液成链情况不同，颗粒体积百分率越大，模拟时所成通链越多，支链、孤链和单个粒子越少.因此，在充分考虑粒子沉降性的基础上，在条件容许的范围内，应该尽可能地增大颗粒的体积百分率.

c.磁流变液受到剪切时，链逐渐向剪切方向倾斜，部分链发生断裂，同时断链、支链、孤链和单个粒子等又重组生成新链，低剪切速率下，旧链的断裂和新链的生成基本上达到动态平衡的状态，但是支链、孤链和单个粒子几乎始终存在.

d.高剪切速率下，粒子向剪切方向的倾斜程度变大，但是通链减少，新链的生成速度明显跟不上旧链的断裂速度，与宏观表现高剪切速率下，随着剪切速率的增加，磁流变液的剪切应力下降相吻合.

e.单链的剪切强度先增大后减小.磁流变液的剪切屈服应力随磁感应强度的增大而增大，随颗粒体积百分率的增大而增大.

[1]汪建晓，孟光.磁流变液研究进展[J].航空学报，2002，23(1):6-12.(WANG Jian-xiao，MENG Guang.Research advances in magnetorheological fluids[J].Acta Aeronautica Et Astronautica Sinica，2002，23(1):6-12.(in Chinese))

[2]汪建晓，孟光.磁流变液装置及其在机械工程中的应用[J].机械强度，2001，25(1):50-56.(WANG Jian-xiao，MENG Guang. Magnetorheological fluid devices and their applications in mechanical engineering[J].Journal of Mechanical Strength，2001，25(1):50-56.(in Chinese))

[3]李金，张华良.磁流变液研究与应用[J].上海大学学报:自然科学版，2004，10(1):21-25.(LI Jin，ZHANG Hua-liang.Study and application of magnetorheological fluids[J].Journal of Shanghai University:Natural Science Editions，2004，10(1):21-25.(in Chinese))

[4]张平.磁流变液的研发与应用[J].功能材料信息，2006，3(1):19-22.(ZHANG Ping.Study and application of magnetorheological fluids[J].Functional Materials Information，2006，3(1):19-22.(in Chinese))

[5]裴畅贵，郭张霞.磁流变液特性分析[J].机械管理开发，2007(2):24-25.(PEI Chang-gui，GUO Zhang-xia.Behavior analysis of magneto-rheological fluids[J].Mechanical Management and Development，2007(2):24-25.(in Chinese))

[6]RABINOW J.The magnrtic fluid clutch[J].ALEE Transaction，1948，67:1308-1315.

[7]GINDER JM，DAVID L D.Shear stress in magnetorheological fluids[J].Role of Magnetic Saturation Appl Phys，1994，65(26):2410-2412.

[8]ROSENSWEIG R E.On magnetorheology and electrorheology as states of unsymmetric stress[J].J Rheol，1995，39(l):179-192.

[9]BOSSIS G，LNAIRE E.Yield stresses in magnetic suspensions[J].J Rheol，1991，35(7):1345-1354.

[10]LEMAIRE E，BOSSIS G.Yield stress andwall effects in magnetic colloidal suspensions[J].J Phys D:ApplPhys，1991(24):1473-1477.

[11]KLINGENBER G D J，ZUKOSKI C F.Studies on the steady-shear behavior of electrorheological suspensions[J].Langmuir，1990(6): 15-24.

[12]阮中尉.基于BCT模型的磁流变液剪切应力预测理论研究[D].武汉:武汉理工大学，2006.

[13]赵四海，方佳雨.一种磁流变流体链化模型的研究[J].润滑与密封，2006(11):108-110.(ZHAO Si-hai，FANG Jia-yu.Theoretics study on the model of magnetic flocculation of magneto-rheological fluid[J].Lubrication Engineering，2006(11):108-110.(in Chinese))

[14]陈伟俊.适用于直线电机阻尼控制的磁流变液的技术研究[D].广州:广东工业大学，2007.

[15]FUST E，GAST A.Micrlmechanics of magnetorheological suspensions[J].Physical Review E，2000，61(6):6732-6739.

[16]方生，张培强.旋转磁场作用下磁流变液颗粒运动及结构演化的模拟[J].化学物理学报，2001，14(5):562-566.(FANG Sheng，ZHANG Pei-qiang.Simulationof the structure and the dynamicsof the particles ofmr fluids in rotating magnetic fields[J].Chinese Journal of Chemical Physics，2001，14(5):562-566.(in Chinese))

[17]SONIA M，CALDERON S.Rotational dynamics in dipolar colloidal suspendions:video microscopy experiments and simulations results[J]. Non-Newtonian FluidMech，2002，102:135-148.

[18]刘望一.流体力学:下[M].北京:北京大学出版社，2000:46-90.

[19]张跃，谷景华.计算材料学基础[M].北京:北京航空航天大学出版社，2007:50-89.