通气超空泡洞壁影响及其比尺效应数值模拟

杨 明，于开平，周景军，樊久铭，万小辉

(哈尔滨工业大学航天学院，150001哈尔滨，58129493@163.com)

超空泡航行体在水下运动时随着速度的提高，航行体周围压强逐渐下降到水的饱和蒸气压以下从而使水气化，但是要生成包围整个航行体的自然超空泡需要很高的速度，对于目前的推进技术很难达到.Reichardt［1］首先提出了通气超空泡的概念，即向泡内注入空气从而可以使航行体在速度较低时就能生成超空泡.目前对于超空泡的研究主要是通过试验完成的.国内外的研究机构利用水洞试验进行了大量的通气超空化试验［2－6］，获得了大批试验数据，总结出了一系列经典的经验公式，但实际当中很多情况都无法进行有效试验验证，水洞试验存在一定的局限性，数值仿真可以很好的解决上述困难，对试验进行很好的补充.陈鑫等［7］基于均质平衡流理论，利用二维模型水洞中没有考虑壁面黏性作用下的洞壁效应对通气空化数的影响进行了研究.胡世良等［8］基于均质平衡流理论采用VOF方法，通过增加来流速度改变弗鲁德数的大小，研究了重力效应对空泡形态的影响.黄海龙等［9］采用混合网格，对均质流域进行求解，模拟了重力场中三维三相通气空泡.从以上可以看出，利用数值仿真研究空化的文章很多，但主要采用均相流模型，目前还未见有对水洞中通气超空泡比尺效应进行定性研究的报道.

本文采用分相流模型和SST湍流模型，考虑了水－气两相间的相互作用、重力效应及洞壁的黏性作用，研究了不同湍流模型对通气率的影响，对不同模型比例的通气超空泡和洞壁影响进行了研究.

1 数值仿真模型

1.1 控制方程

由于来流速度较低，自然空化数较高.自然空化非常微弱，完全可以忽略，数值仿真完全采用气－液两相流模拟，通入的气体为1个标准大气压下的空气，水与空气的温度恒定为25℃.环境压力为1个大气压，因此不考虑空气的可压缩性，控制方程为气相和液相连续性方程、动量方程、体积分数方程以及湍流方程.

连续性方程:

动量方程:

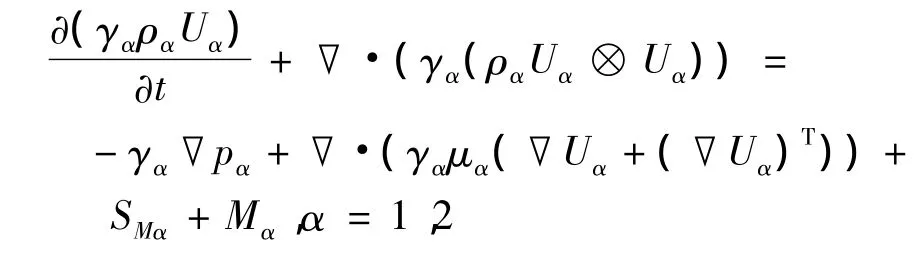
体积分数方程:

1.2 SST湍流方程

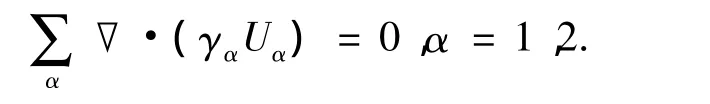
SST湍流模型是在Wilcox k－ω湍流模型和Baseline(BSL)k－ω模型的基础上发展而来的.Wilcox k－ω湍流模型求解2个输运方程，1个是湍动能k的输运方程，另1个是湍流频率ω的输运方程.

k方程为

ω方程为

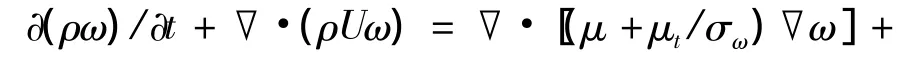
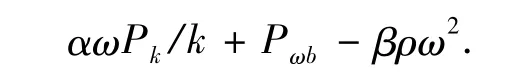
其中Pk为湍流的生成速度.其他模型中的常数分别为

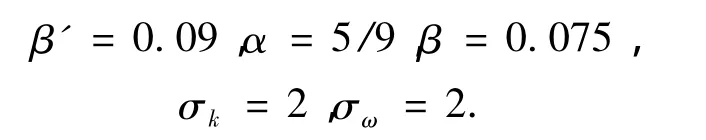
Wilcox湍流模型的主要问题是它对自由来流条件非常敏感.入口处指定的ω值的不同，可能会导致结果发生很大变化.为了避免这个问题.Menter发展了一种混合函数，在近壁区域采用k－ω模型，在外层区域采用k－ε模型.它包括从k－ε模型向k－ω模型的转换同时也增加了一系列额外的方程.Wilcox模型乘上1个混合函数F1，转换的k－ε模型乘上函数1－F1.函数F1在近壁区域等于1，在边界层外面逐渐减小到0，这就是BSL湍流模型.

BSL模型中的各个系数是Wilcox模型和kε两种模型对应系数的线性叠加.三种模型系数分别以Φ3、Φ2和Φ1表示，则

基于k－ω模型的SST湍流模型不但可以求解湍流剪切应力并且在预测各种压力梯度下的流动分离时也具有很高的精度.BSL模型尽管结合了Wilcox模型和k－ε模型的优点，但是很难预测光滑表面的流动分离问题.主要的原因是两种模型都没有考虑剪切力的输运.它将导致过高的预测涡粘度.通过对涡粘公式进行限制，可以得到合适的输运特性.受限的涡粘公式为

F2与F1一样同样为混合函数.S为应变的不变测度.与BSL k－ω湍流模型相似，SST湍流模型同样引入了一种混合函数.

混合函数对于该方法的应用至关重要.其形式依赖于最近壁面的距离以及流动变量.

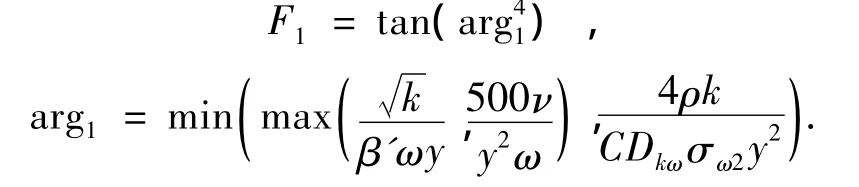
式中y为距离最近壁面的距离，ν为运动粘度，

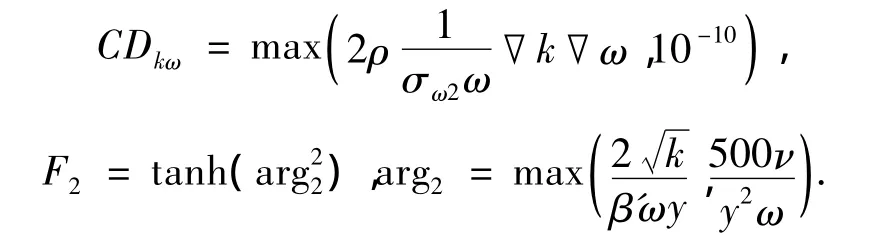
2 模型、网格及边界条件

本文计算了绕圆盘空化器和航行体的通气空泡流动，航行体仿真模型外形及通气装置参照文献［7］，如图1所示，由圆盘空化器、锥段、柱段及喷管组成.模型的空化器直径为18 mm，弹体最大直径为42 mm，弹体最大长度为520 mm，为了进行比尺效应研究，将该尺寸作为参考尺寸，并设其为比例为1模型的尺寸，比例为0.75模型的各尺寸则为参考尺寸的0.75倍.令Dn为空化器的直径，Lc为空泡的最大长度，Dc为空泡的最大直径.

图1 仿真模型

网格全为结构化网格，如图2所示，质量在0.65以上.分别比较了200万、100万、80万、60万的网格对计算结果的影响，经比较80万与60万的计算结果差别较大，100万与80万的计算结果差别较小，而100万与200万的网格几乎无差别，所以本文模拟采用100万到130万的网格进行了模拟.

图2 前端空化器网格放大

边界条件设置如图3所示，由于来流速度较低，不考虑可压缩性，因此上游采用速度入口，下游为压力出口，当模拟水洞时，外边界为无滑移壁面边界条件，当模拟无限大流场时，采用比例为1的模型，外边界为扩大了的压力开口边界条件.

图3 边界条件设置

3 数值仿真结果与分析

3.1 湍流模型对通气率的影响

本文首先模拟了绕圆盘空化器的通气空泡流动，比较了不同湍流模型对通气率的影响.本次仿真结果将采用目前认为最为可靠的Epshtein半经验公式进行验证，如下所示:

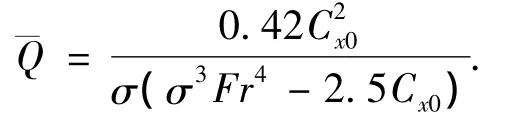
3.2 通气率对超空泡形态的影响

表1为比例为1的模型随着通气量的增加超空泡的发展过程.可以看出，当通气率较小，空泡未充分发展时，空泡尾部主要以回注射流方式泄气，随着通气量的增大，开始生成局部空泡，一直增大到某一临界值时，空泡迅速跳变形成包裹整个航行形体的超空泡，在超空泡生成双窝管出现后，随着通气率增加呈缓慢增大趋势.

表1 不同通气率下超空泡形态

图5为来流速度保持不变条件下，增加通气量通气超空泡发展过程中，通气率与无量纲空泡长度对比图，图中6个数据点与表1中6个图片是对应的，可以看出超空泡发展过程中存在临界通气率，在临界通气率处，泄气方式发生变化，由回注射流变为双窝管.

3.3 不同模型比例和洞壁对超空泡形态的影响

图6～8为不同模型比例和无界流场在相同通气率下的空泡形态及不同通气率下空泡的无量纲长度与直径的比较.由图可知，比例0.75模型在空泡的长度和直径上都要大于比例1模型，是因为受弗鲁德数和洞壁的影响.弗鲁德数的定义为Fr=，模型比例为1、0.75和0.50时，弗鲁德数分别为27.9、32.0和40.0.随着弗鲁德数的增加，在相同的通气率条件下，空泡的长度逐渐增大，与文献［10］结论一致.从上图中也可看出，无界流场情况下空泡的长度和直径都要大于比例为0.75和1.00的模型，是洞壁导致的结果.空化数σ的公式为σ=(p∞－pc)/0.5·ρv2，由于洞壁的存在导致了流场压力的变化，进而导致了p∞－pc的值变大，使空化数增大，空泡尺寸减小.比例0.75模型的空泡长度和厚度位于无界流场和比例1模型之间，进而验证了上述结论的正确性.

图5 不同通气率下超空泡无量纲长度

图6 不同模型比例和无界流场在相同通气率下的空泡形态

文献［5］、［10］等通过增加来流速度改变弗鲁德数的大小，本文则通过改变模型的特征长度来改变弗鲁德数的大小，从另一角度观察了弗鲁德数的变化对空泡上漂的影响.如图9所示，比例1模型的上偏程度要大于比例0.75模型，与小弗鲁德数上偏程度大结论相一致.而无界流场条件下的空泡上偏程度要大于有洞壁影响的情况，可以认为是洞壁的存在导致了流场压力的变化.

图7 不同通气率下空泡的无量纲长度

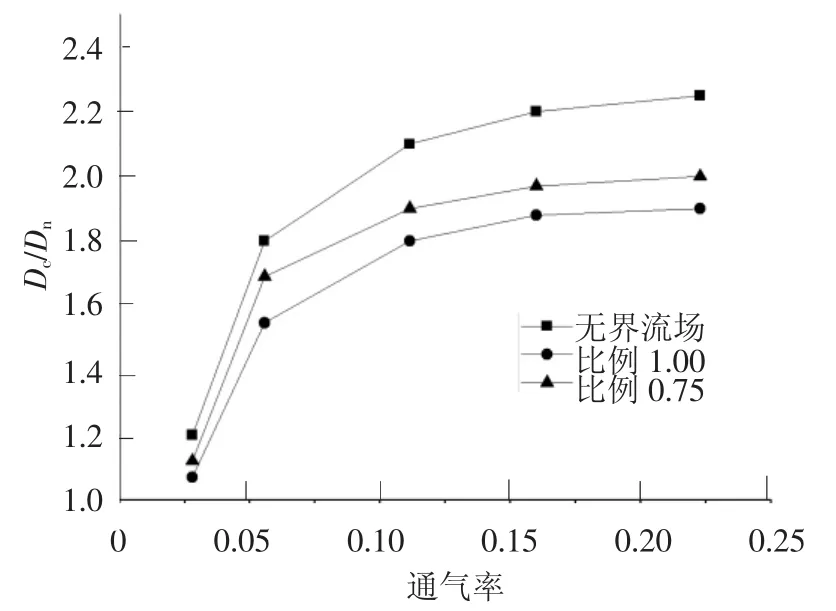
图8 不同通气率下空泡的无量纲直径

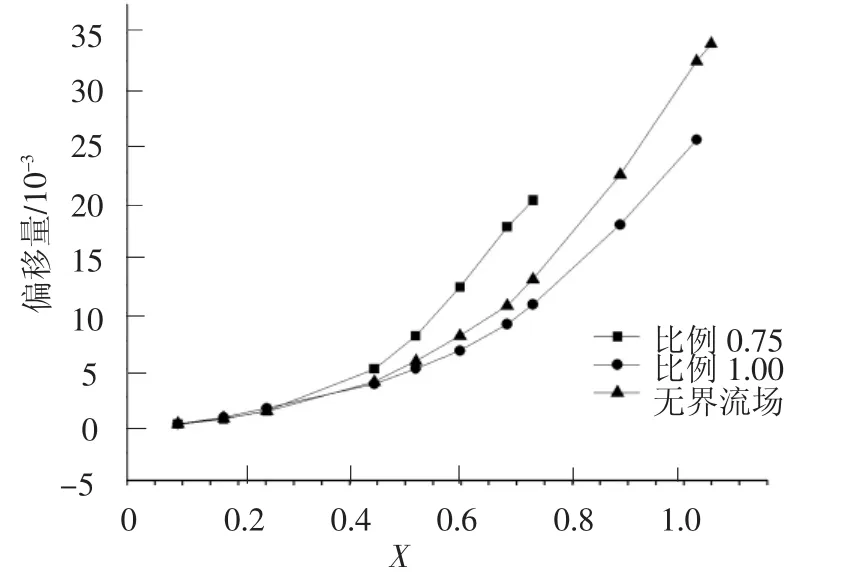
图9 超空泡轴线偏移量

3.4 不同模型比例和洞壁对超空泡减阻效果的影响

图10为不同通气率下空泡的阻力系数.由图可看出，3种条件下的减阻趋势基本相同，都是局部空泡阶段模型阻力随通气率的增加而减小，过渡阶段通气率的微小改变会导致模型阻力的迅速减小，超空泡阶段随着通气率的增加，模型阻力基本保持不变.但是最大减阻效果有差别，如表3所示，比较无界流场和比例1模型所受阻力大小和最大减阻比例发现，由于有洞壁的存在，模型所受的阻力偏大，使得通气超空泡的最大减阻比例偏大;比较比例1模型和比例0.75模型的最大减阻比例发现，缩小模型的最大减阻比例偏大.

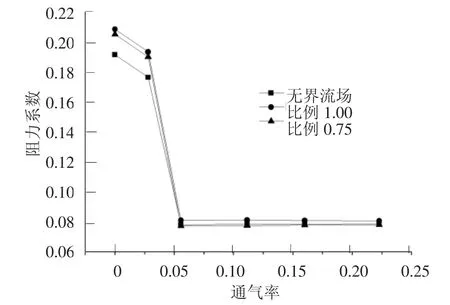
图10 不同通气率下空泡的阻力系数

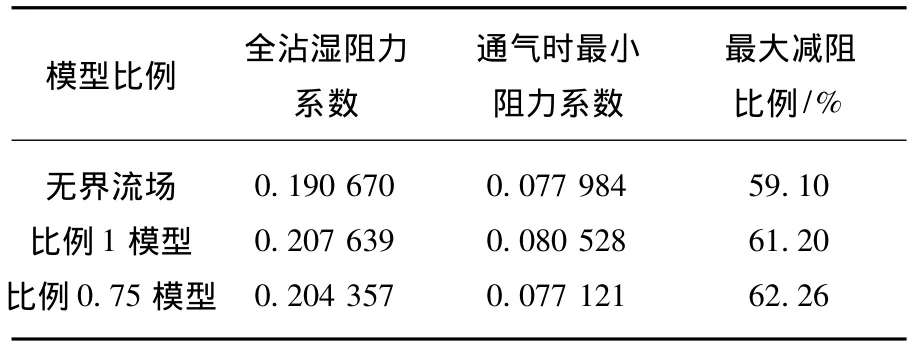
表3 最大减阻比例

4 结论

基于RANS方程，采用分相流模型和SST湍流模型，考虑了水－气两相之间的相互作用及重力效应，对通气超空泡的洞壁影响及其比尺效应进行了研究.研究了不同湍流模型对通气率的影响，比较了水洞中不同模型比例和无界流场中在空泡形态和阻力上的差别.结果表明:

1)小比例模型在空泡的长度和直径上都要大于大比例模型;通过改变模型的特征长度来改变弗鲁德数的大小，从另一角度考察了弗鲁德数对空泡上偏的影响，与小弗鲁德数上偏程度大结论相一致.

2)洞壁的存在导致了流场压力的变化，进而导致了通气空化数变大，使得空泡的长度和直径都变小，但无界流场条件下的空泡上偏程度要大于有洞壁影响的情况.

3)在减阻效果方面，由于有洞壁的存在，使模型所受的阻力偏大，使得通气超空泡的最大减阻比例偏大;比较不同比例模型的最大减阻比例发现，缩小模型的最大减阻比例偏大.

在本文数值模拟的过程中发现，比例1模型、比例0.75模型和比例0.5模型在相同的小通气量的条件下，当比例1模型和比例0.75模型生成空泡时，比例0.5模型只是在模型的表面生成部分气层，前端空化器处并没有出现空泡，直到通气量较大时空化器处才开始出现空泡，与贾力平等［13］在实验中观察到的现象是一致的.本文只是对比尺效应和洞壁对通气超空泡的影响进行了定性的研究，对比尺效应和洞壁带来的影响修正还需要进一步的研究.

［1］REICHARDT H.The laws of cavitation bubbles as axially symmetrical bodies in a flow［R］.Great Britian:［s.n.］，1946(766):322－326.

［2］SAVCHENKO Y N.Experimental Investigation of Supercavitating Motion of Bodies［R］.Brussels:VKI Special Course on Supercavitating Flows，2001.

［3］WOSNIC M，SCHAUER T.Experimental study of a ventilated supercavitating vehicle［C］//5th Intermational Symposium on Cavitation.Osaka:［s.n.］，2003.

［4］KIRSEHNER I N，GISEKE T A，KUKLINSKE R，et al.Supercavition research and development［C］//Undersea Defense Technologies Hawaii 2001.Waikiki，HI:［s.n.］，2001.

［5］袁绪龙，张宇文，王育才，等.水下航行体通气超空泡非对称性研究［J］.力学学报，2004，36(2):146－150.

［6］王海斌，王聪，魏英杰，等.轴对称航行体通气超空泡的特性实验研究［J］.工程力学，2007，24(2):166－171.

［7］CHEN Xin，LU Chuanjing，LI Jie，et al.The wall effect on ventilated cavitating flows in closed cavitation tunnels［J］.Journal of Hydrodynamics，2005，20(5):561－566.

［8］胡世良，鲁传敬，潘展程.通气空泡重力效应研究［J］.水动力学研究与进展，2009，24(6):786－792.

［9］黄海龙，魏英杰，黄文虎，等.重力场对通气超空泡影响的数值模拟研究［J］.哈尔滨工业大学学报，2007，39(5):800－803.

［10］王海斌，王聪，魏英杰，等.水下航行体通气超空泡的实验研究［J］.船舶力学，2007，11(4):514－520.

［11］张学伟，张嘉钟，王聪，等.通气超空泡形态及其稳定性实验研究［J］.哈尔滨工程大学学报，2007，28(4): 381－387.

［12］张学伟，魏英杰，张庆丽，等.通气空泡发展过程及其水动力影响［J］.哈尔滨工业大学学报，2007，40(7): 1031－1035.

［13］贾力平，于开平，张嘉钟，等.空化器参数对超空泡形成和发展的影响［J］.力学学报，2007，39(2):210－215.