小波变换的时频分析及其在实际中的应用

2011-03-13徐博尧杨刚李欣欣

中国传媒大学学报(自然科学版) 2011年2期

徐博尧，杨刚，李欣欣

(中国传媒大学，北京 100024)

1 引言

在信号分析与系统设计中，Fourier分析得到广泛应用。在分析方法上，根据信号的时域抽样定理和频域抽样定理，可以将两种信号的Fourier变换的计算转换为有限长序列的离散Fourier变换的计算。从而可以从数值上实现对信号的与系统的频域分析。随着科学技术的发展和应用领域的扩展，需要对非平稳信号和事变信号进行分析研究，以期获取信号在不同瞬间对应的频谱分布，从而了解信号的频率和能量随时间变化的规律。但是在利用傅里叶变换分析这些突变信号的时候，无法有效的反映信号在某些瞬间的突变。因为在信号的Fourier变换中，反映的是信号的总体平均信息，信号频谱中的任一频率分量都是对信号整个时域定义区间上的Fourier积分或求和，信号在时域上某些瞬间的突变，在信号的频谱上虽然有所反映，但是一般并不明显。此外，即使能够计算出信号的频谱，但由于信号的瞬间突变而发生了改变，也无法从信号的频谱中确定信号在时域的突变时刻，即在信号的Fourier变换中，无法反映信号的时间特性。

时频分析实际上是将一维的时间信号映射到二维的时间尺度上，以便看清在细小时间内信号频率的变化，这对于非平稳和时变信号来讲是非常有用的。

2 小波变换简介

2.1 综述

小波分析法是一种非常有效的信号时频分析方法，在信号处理、语音分析、模式识别等领域有着广泛的应用。它是一种窗口大小固定，但其形状可以改变，时间窗和频率窗都可以改变的时频局域化分析方法，即在低频部分具有较高的频率分辨率和较低的时间分辨率，在高频部分具有较高的时间分辨率和较低的频率分辨率，这正符合低频信号变化缓慢，而高频信号变化迅速的特点。在大尺度下，可以将信号的低频信息全局表现出来，在小尺度下，可以将高频局部特性表现出来因此小波变换被誉为“数学显微镜”［1］。总体上说，小波变换比短时傅里叶变换具有更好的时频特性窗口。对于平稳和非时变信号而言，可以用傅里叶变换分析它的时频域性质。但是对于非平稳和时变信号来说，傅里叶变换就作用不大了，它无法反映信号在某些瞬间的突变。因为我们需要了解信号在不同瞬间所对应的频谱分布，从而了解信号的频率和能量随时间变化的规律特征。因此我们使用小波变换。小波变换对信号具有良好的自适应性。

2.2 小波变换公式及基本原理

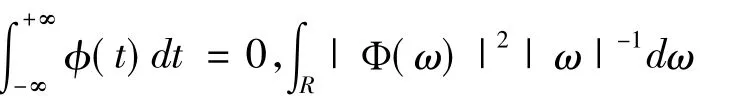
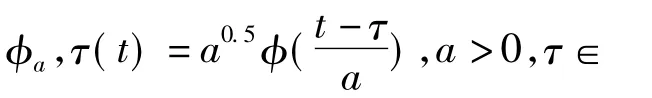
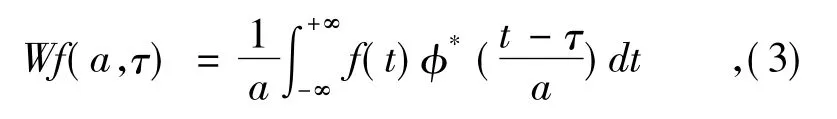
其中a为尺度参数，τ为平移参数。φaτ(t)依赖于a，τ的小波基函数。它们是一组φ(t)经过伸缩平移得到的函数序列。

时频分析中常用的是连续小波变换，在实际信号处理中常用离散小波变换及其逆变换。连续小波变换表达式为:

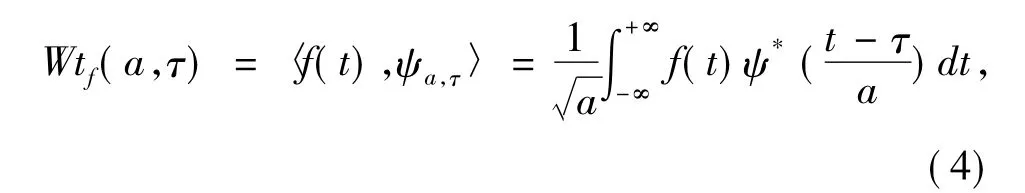
离散小波变换表达式为:

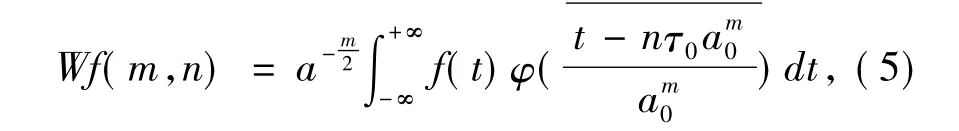
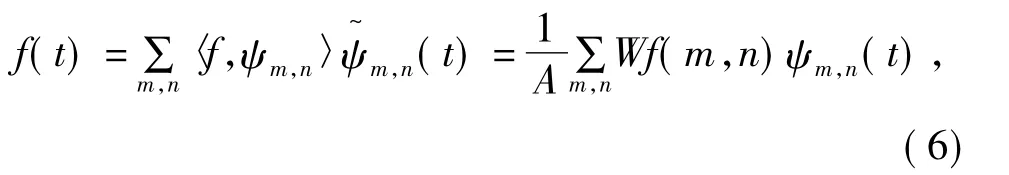
由以上我们可以看出来，小波变换时一种积分变换。小波基并不唯一，即存在许多不同特性的小波基函数，这是它与Fourier变换不同的地方。小波基存在尺度和平移τ两个参数，所以函数经过小波变换，就可以将一个时间函数投影到时间——尺度平面上，从而同时获得信号的时间和频率分量，实现信号的时频分析［2］。

3 小波变换的时频分析

3.1 对频率时变信号做连续小波变换

原信号为一个频率随时间增大的函数，其连续小波变换系数如图1所示。所使用的小波基函数为Daubechies系列的小波基db10。

源程序如下:

wname= ‘db10’;

clear all;

M=2^11;a(1:1:M)=0;

b(1:1:M)=0;

y(1:1:M)=0;

K=400;

Kc=10;

N=10;

L=24;

a(1)=0.5*K;

for i=2:1:M

a(i)=a(i－1)+K;

end

b(1)=Kc+a(1);

for i=2:1:M

b(i)=b(i－1)+(Kc+a(i));

end

for i=1:1:M

y(i)=floor(2^N*cos(2*pi/(2^L)*b(i)));

end

figure(1);subplot(211);plot(y);axis(［0 M，－2^N －100 2^N+100］);

subplot(212);cwt(y，1:1:512，wname，‘plot’);colorbar;

figure(2);subplot(211);plot(y);axis(［0 M，－2^N －100 2^N+100］);

totalscal=512;

wcf=centfrq(wname);

cparam=2*wcf*totalscal;

a=100:－1:1;

scal=cparam./a;

coefs=cwt(y，scal，wname);

f=scal2frq(scal，wname，1/fs);

xlabel(‘时间 t/s’);

ylabel(‘频率 f/Hz’);

subplot(212);imagesc(t，f，abs(coefs));

title(‘小波时频图’);

colorbar;

原信号如图1中的(a)所示。

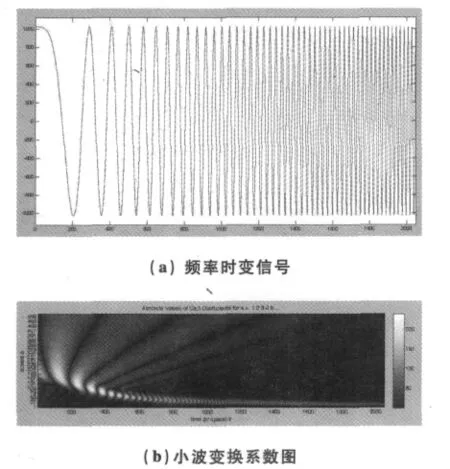
图1 对频率渐增信号使用db10小波基函数进行小波变换

从图1中可以看出来，使用小波变换可以清楚的将信号所包含的频率成分都识别出来。图中，亮度高的地方，小波变换系数大;反之则系数小。因此，我们可以看出小波系数大致在时间——尺度上的分布情况［4］。信号在时域的能量等于信号在小波变换域里格展开分量的能量之和，满足能量守恒。我们还可以看到，随着原始信号在较低尺度信号空间上的投影，其对应信号的信号分量，相应的平移步长较宽，因而时间分辨率，频率分辨率逐渐变高，所以如图所示，信号的高频分量有了较高的时间分辨率，而信号中低频分量有了较高的频率分辨率。这说明，信号的小波变换能够根据信号的变化特性自动调整时窗和频窗，因而可以有效的实现信号的时频分析。

为了更清楚的看清楚不同频率成分的时间——尺度投影，再给一个只含两种频率成分的2FSK信号做小波变换，所选的小波基仍为db10。源程序省略。效果如图2所示。

从上面可以看出，两种频率成分被区分的非常清楚，频率大小和时间分辨率的关系也在图中体现出来。

3.2 使用不同小波基对原信号进行时频分析

小波基的选择并不是唯一的，这为信号的小波分析提供了更多的灵活性，同时也给实际应用的选择带来了一定的难处。下面讨论不同小波基分析的时频效果。

3.2.1 使用 coifl小波基

对原频率渐增信号使用coifl小波基变换后效果如图3所示。

3.2.2 使用sym8小波基

对原频率渐增信号使用sym8小波基变换后效果如图4所示。

3.2.3 使用dmey小波基

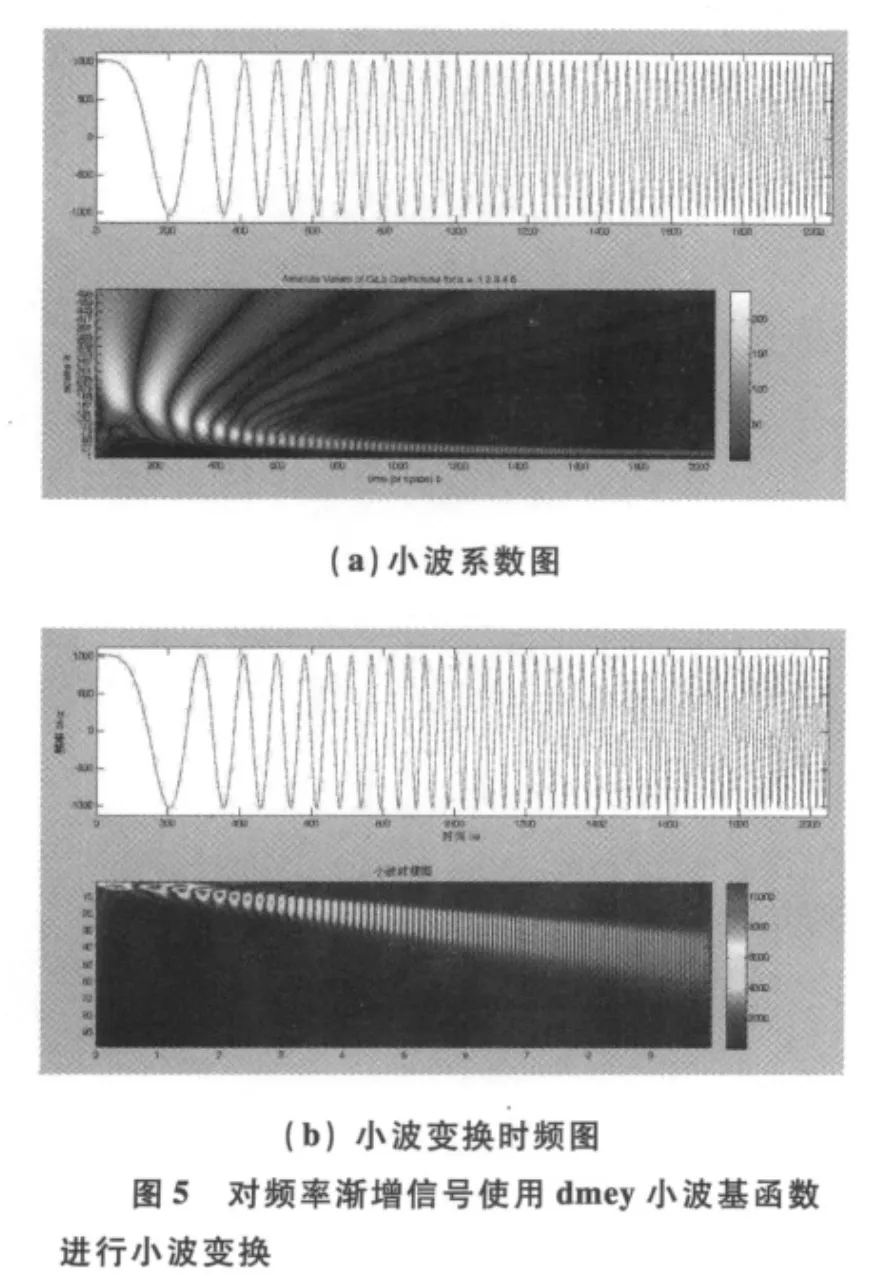
对原频率渐增信号使用dmey小波基变换后效果如图5所示。

仔细比较图1，图3，图4，图5，同一个信号，使用不同的小波基对其进行小波变换，则变换后小波系数不一样，对高低频的分辨率也不一样，出来的时域分辨度也不一样。小波函数的尺度越高，其对应信号中越精细的细节。因此要根据具体情况适当选择小波基函数。就原频率渐增信号而言，选择db10小波基在所选择的小波基中是效果最好的。

小波基函数具有非唯一性，它使得小波分析具有更加广泛的适应性，可实现对于不同特性的信号采用不同的小波基信号，从而使得变换后的小波系数更稀散，更加易于信号的分析和处理。因此，小波分析具有其独特的优点，特别是对于非平稳信号，有着明显的优越性。

4 小波变换和其他变换的比较

图6为原频率渐增信号经汉明窗的STFT变换后的结果。

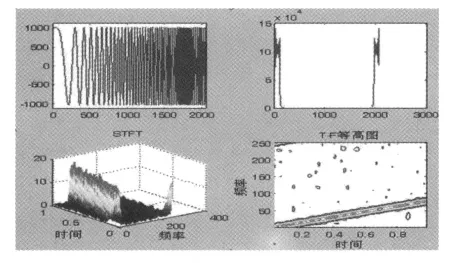
图6 频率渐增信号经汉明窗的STFT变换的频谱、三维、等高图

小波变换和其他变换一样，都是将信号展开为一组正交信号的线性叠加。但是Fourier技术是将一维连续变量映射成一维的离散序列;而小波展开则是将一维连续变量映射为而为的离散序列。正式这种二维表示使得小波展开同时具有时间和频率的分辨率。

如图6，STFT的时域分辨率和频域分辨率是相互制约的。STFT变换可以同时具有时频分辨率，但是其时频窗口的形状对于不同的信号分量保持不变。其时间分辨率由信号的STFT中的时窗宽度决定，时窗宽度越窄，时间分辨率越高;频率分辨率则由窗函数频谱宽度决定。由窗函数特性可知，窗函数的时域宽度越窄，窗函数频谱就越窄，因此STFT无法同时获得较高的时间分辨率和频率分辨率。而小波变换则能够对不同信号实现时频窗口的自动调整。

因此只有小波变换的时频窗能够较好的满足非平稳及时变信号时频分析的需求。