基于地形的自适应压缩和实时可视化

郑新，王钰，王晓东

(北京师范大学图像处理和模式识别实验室，北京 100875)

1 引言

地形渲染是虚拟现实的一个重要组成部分。随着虚拟现实技术的进一步使用和数据获取设备分辨率的不断提高，在虚拟环境中被渲染的数据越来越多。这些数据超出了个人计算机内存的装载能力，不得不把大批量的数据进行分批装载。频繁的读取数据使得渲染的效率受到很大影响。

为了降低数据读取的频率，许多人提出了他们的数据压缩方法，比如降低存取缺失率的高速缓存高效算法［1］，基于顶点聚类的网格简化方法［2，3］，基于拓扑信息的网格简化算法［4］，C － BDAM［5］和 geometry clipmap［6］等等。

二十世纪八十年代，Mallat首次将小波变换引入图像处理。很好的时频局部化特征和多分辨率的分析方法使得小波变换被广泛地应用于图像压缩［1－6］。然而作为传统小波变换的离散小波变换(DCT)往往会导致浮点系数，这增加了计算的复杂度并且不适合进行高效的无损压缩。为了解决这个问题，I.Daubechies和W.Sweldens提出了一种提升格式(LS)［4］。基于这种提升格式，一种新型的变换被提了出来，称作整数小波变换(IWT)。IWT降低了计算复杂度，能高效地执行DCT，还能够支持图像的无损压缩。所以在我们早期的工作中［7］就是使用这种方法对地形进行无损压缩的。但是在此工作中没有考虑地形平坦、起伏等变化，尤其是复杂区域的地形，而是使用了相同的分辨率对地形进行规则化统一渲染。为了克服了这个缺点，本文使用限制四叉树三角化方法(RQT)［8］，提出了一种高效的海量地形自适应压缩和渲染算法，该算法除了具有较高的压缩比和运行效率，对于海量地形漫游也能达到高效、实时、连续的视觉效果。

本文的组织结构如下:第二部分将介绍基于整数小波变换的限制四叉树三角化。第三部分讨论地形压缩，基于视点的多分辨率解压缩和实时渲染中的场景更新算法。最后两部分将给出一些实验结果，并对本文的工作作出一个简单的总结。

2 基于整数小波变换的限制四叉树三角化

2.1 整数小波变换

小波变换是一种用来描述多分辨率分析中的1D/2D信号的数学工具。通过一系列的低通和高通滤波器，小波变换能够把一幅图像分解为一个低频子带和三个高频子带。由于原始图像的大部分信息集中在低频子带中，则低频子带能够以同样的方式被分解，并且原始图像的合成可以被认为是分解过程的反过程，如图1所示。

图1 灰度图像小波分解示意图

与传统的小波变换相比，整数小波变换除了能够进行多分辨率的分解和合成外，还有一些其他的优点，比如，整数小波变换使用提升格式。提升格式是一种设计小波和执行离散小波变换的技术，它的每一步变换都是可逆的。这意味着能够毫无误差地将数据进行合成。本文压缩方法中使用的5/3无损小波能够解释这个属性。5/3小波提升格的正变换格式如下:

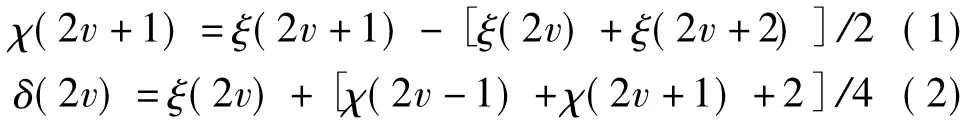
逆变换格式是:

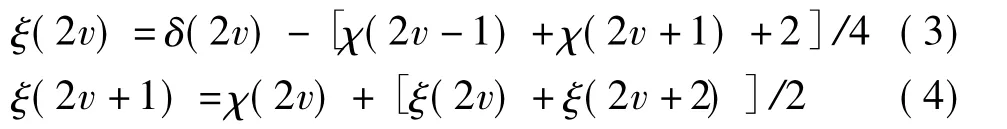
从上面的分析可知，整数小波变换能够仅仅占用常数值的内存开销直接在内存中处理数据，而且它还具有很好的合成性，也能进行多分辨率分析。因此它非常适合用在地形压缩和渲染中。

2.2 限制四叉树三角化

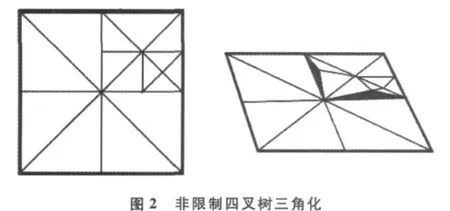
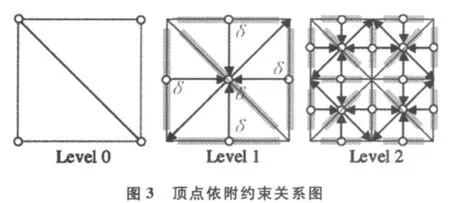
图2所示是一个平面四叉树递归三角化的例子。这里定义一个变量δ，它表示该顶点的高度值和垂直方向邻接4个顶点平均高度值的差值。如果δ比给定的阈值大，那么相对应的顶点就分裂。但是如右图所示在对应的三维平面上就会出现裂缝。为了避免相邻两个不同的分辨率节点在邻接处的裂缝现象，采用限制四叉树方法进行动态的网格构造。每个顶点依赖相同层或是下一层的两个其它顶点，这意味着如果选定某一细节层次中的某一顶点，那么与其有约束关系的顶点也应该被选定。图3表示顶点之间的相互约束关系。

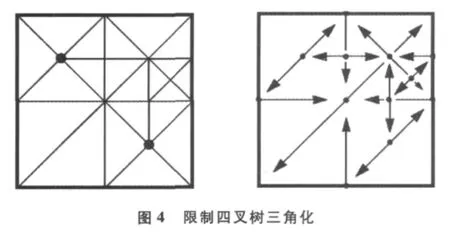
通过连续地限制点的选择区域，顶点的依附约束关系能消除裂缝，从而得到一个匹配的三角化结果。图4表示利用限制四叉树消除图3中裂缝的方法，其中右边的图形是顶点之间相互约束的关系图。由于三角化过程是隐式给出的，所以它能被高效地合成。

2.3 基于整数小波变换的限制四叉树

地形数据往往存储为被看做灰度图像的DEM数据。如图1所示，变换的每一层被分解成一个低频部分和三个高频部分。仔细分析可以发现，小波系数其实代表着地形变化特征。地形变化比较复杂的区域，小波系数就比较大，相反地形比较平坦的区域，小波系数基本相同而且比较小。

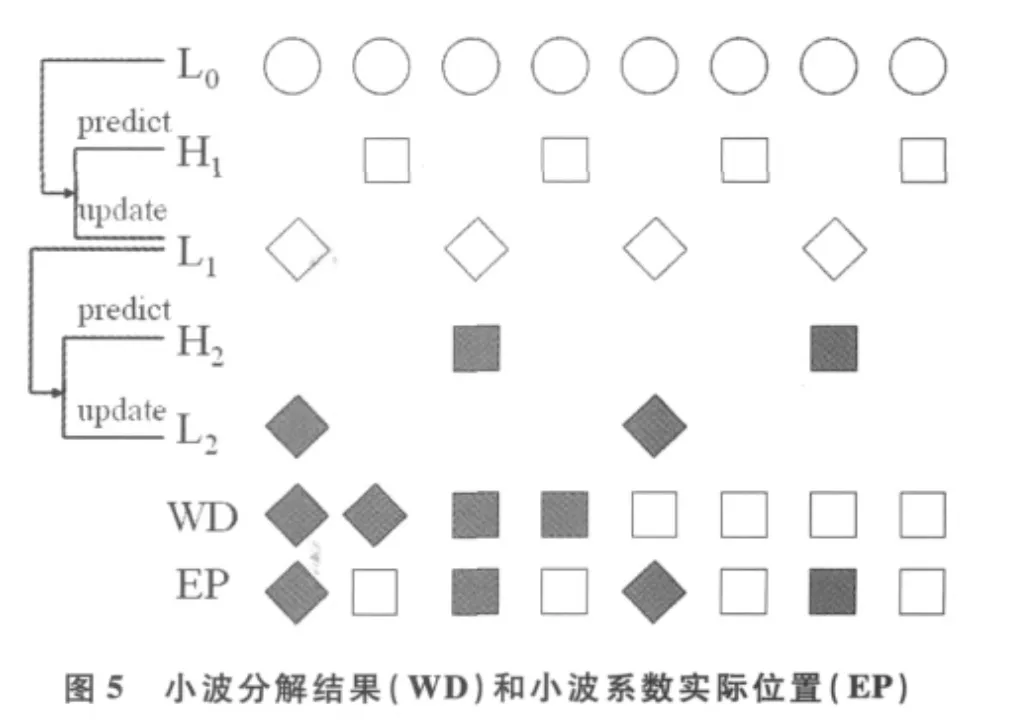
如前所述，小波系数含有时域和频域中的信息。它的频域位置对应着分辨率的层次，而它的时域位置是从变换域中对应的子带的位置推导出的。图5所示是对图2进行1D小波提升算法分解8个顶点后的结果(WD)和小波系数的实际位置(EP)。

由上述公式(1)，(2)，(3)和(4)可知，沿着行和列的方向相继执行1D小波变换后就能得到2D小波系数。对图1进行2D整数小波变换的结果和小波系数的实际位置如图6所示。这里○，□，和△各自表示一次变换中的子图HL1，LH1，和HH1。而

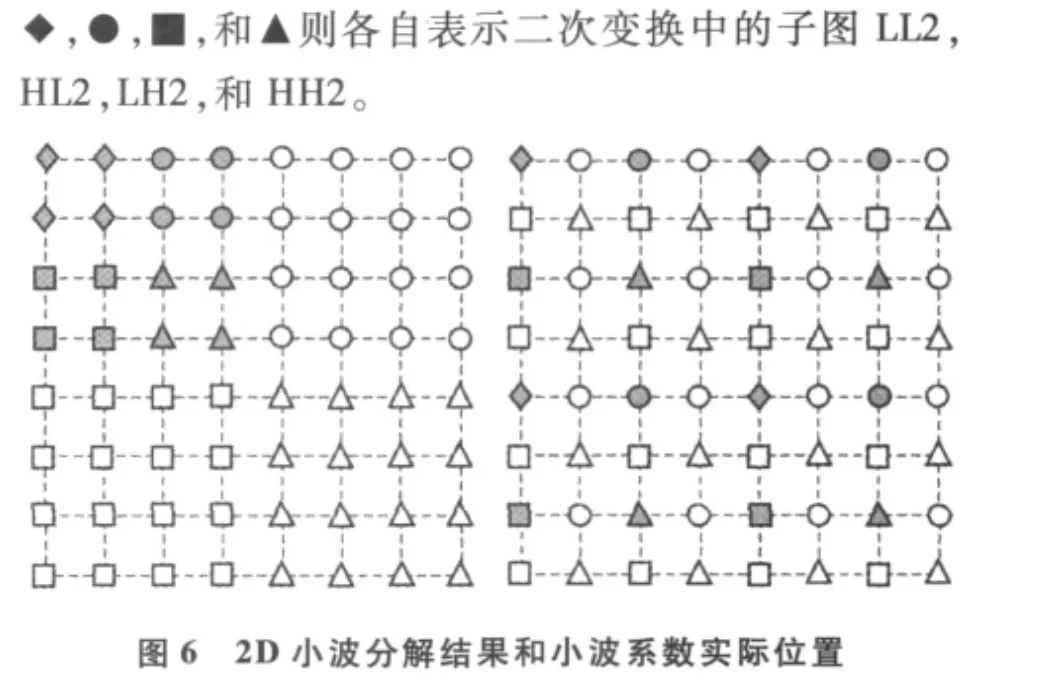
经过这一步后，每个系数都与地形上相应的顶点构成一一对应的关系，而且系数的量就代表着顶点的高度变化，也就是地形特征。

从图7可以看出，由对角线的5个系数构成的矩形单元格组成了整个的网格结构。其中HL，LH，和HH的系数分别表示对应顶点水平、垂直和对角线方向上的变化。仔细分析图3和图7可以发现，δ和位于相同位置的小波系数的量有相似的地形表面复杂度。

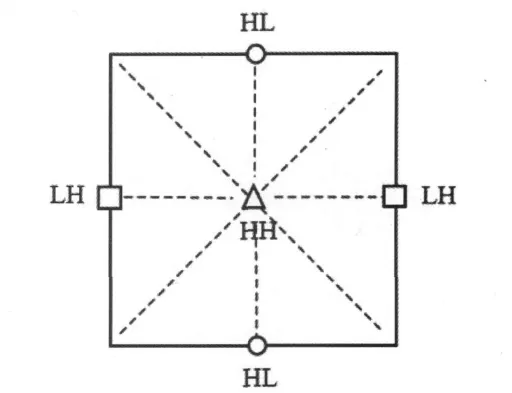
图7 由5个系数组成的矩形单元格

对于网格的构造，本文采用基于小波系数的限制四叉树算法。首先根据顶点对应的小波系数与给定阈值的比较来判断这个顶点是进行分裂还是合并，然后采用限制四叉树结构的分裂和合并对地形模型进行更新。

3 地形压缩和可视化

3.1 地形压缩

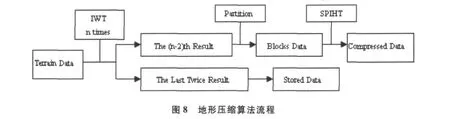
考虑到地形数据非常庞大，我们使用分区压缩方法，因为这种方法能够随机访问压缩的比特流，并且能够调整内存的使用和变换数据的数量。为了解决边界问题，压缩算法在划分之前先对整个地形数据进行n次整数小波变换，然后再把整个的小波系数分离到这些块中(图8)。这里存储最后2次整数小波分解后的数据的目的是构造全景图，也就是当视点所在位置高度非常高的情况。通过第二部分中提到的逆变换公式(3)和(4)，可以直接渲染含有大部分信息的地形数据，然后将第(n－2)个变换小波系数分离到小块中。

在上面所述的基于整数小波变换的限制四叉树算法中，小波系数是唯一需要存储的数据。在图像处理领域，已经有很多经典的基于小波变换的压缩算法。本文所采用的压缩算法是SPIHT(分层树集合分割排序)［9］算法。它利用位平面分层划分的方法，间接实现了空间小波树的比特平面排序，有效地减少了位平面的编码符号集的规模，提高了压缩比。

3.2 地形渲染

本阶段将描述如何使用本文提出的实时地形可视化算法来显示海量地形数据。图9显示了算法的整个流程。

如果需要绘制全景图，只需把存储的数据做整数小波逆变换，得到高度数据后直接绘制即可。随着视点靠近地形表面，地形网格需要细化到精细的分辨率，所以选择视域内的压缩数据并读入内存，进行解压缩和整数小波逆变换得到高度值和限制四叉树结构，完成绘制。当视点移动时，先前的地形网格就通过限制四叉树进行顶点分裂或者合并，从而实现地形模型的更新。

4 实验结果

本文实现采用的地形数据是分辨率为130175×130175的深圳市地形高度图，实现平台是VC6.0和OpenGL，实现环境是 Pentium D 3.0GHz CPU，1024MB内存。

表1 地形数据压缩时间消耗表

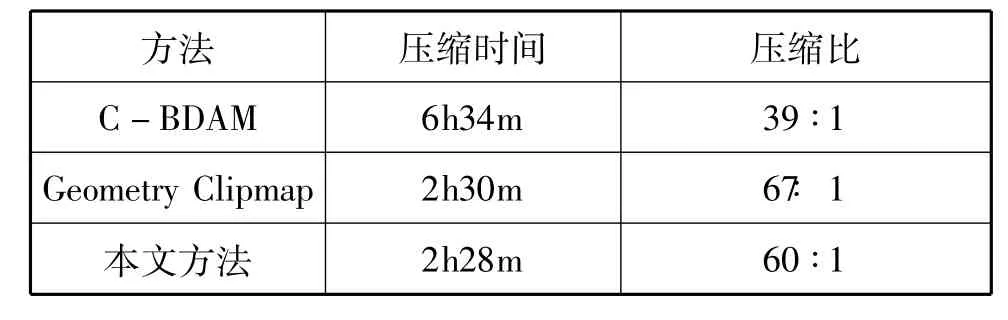
表2 压缩算法对比实验数据表

首先对16G的数据进行10次整数小波变换分解，然后存储第10次LL10(27×27)和第9次LL9(28×28)分解的结果。存储数据的大小为80KB。然后把小波系数划分成大小为1025×1025的块，总共有127×127块。对于每一块都采用SPIHT完成压缩，表1显示了每一步所消耗的时间。

压缩后的数据大小是286MB，与原始数据比为60:1。该算法与 CBDAM［5］和 Geometry clipmap［6］的比较如表2所示。虽然［6］在压缩比上优于本文的算法，但是它采用的是规则网格。在绘制效果上肯定要逊色一些。

5 结论与展望

本文结合整数小波变换和限制四叉树的特点，提出了一种更为科学的基于地形特点的自适应压缩算法，并且能对地形进行实时地渲染。整个绘制过程不仅可以达到实时连续的视觉效果，而且保持着较低的平均内存占用率，但是在地形绘制过程中没有考虑地形的自身遮挡问题。在地面漫游时，地形的遮挡将对地貌的视觉效果产生明显的影响，特别是在地形表面起伏比较大的区域。因此，下一步的目标是使用小波技术进一步改进海量地形压缩和对地形的遮挡进行剔除以达到更好的渲染效果。

［1］ Yoon S E，Lindstrom P，Pascucci V，Manocha D.Cache － oblivious mesh layouts［J］.ACM SIGGRAPH，2005，886 －893.

［2］ Lindstrom P.Out－of－core simplification of large polygonal models［C］.In SIGGRAPH’00 Conference Proceedings，2000，259 －262.

［3］ Lindstrom P.Out－of－core construction and visualization of multiresolution surfaces［C］.ACM Symp on Interactive 3D Graphics，2003，93－102.

［4］ Isenburg M，Lindstrom P.Streaming meshes［R］.In Visualization ’05 Proceedings，2005，231－238.

［5］ Gobbetti E，Marton F，Ganovelli F.CBDAM—Compressed batched dynamic adaptive meshes for terrain rendering［R］.Computer Graphics Forum，2006，333 －342.

［6］ Losasso F，Hoppe H.Geometry clipmaps:terrain rendering using nested regular grids［J］.ACM Trans.Graph 23，2004，769 －776.

［7］ Xiaodong Wang，Xin Zheng，Qian Yin.Large Scale Terrain Compression and Real－Time Rendering Based on Wavelet Transform［R］.2008 International Conference on Computational Intelligence and Security，December 2008，489－493.

［8］ PajarolaR.Large scale terrain visualization using the restricted quadtree triangulation［C］.In:Proceedings of Visualization’98，October 1998，19 －26.

［9］ Said A，Pearlman W A.A new fast and efficient image codec based upon set partitioning in hierarchical trees［J］.IEEE Transactions on circuits and systems for video technology，June 1996，243－250.