冻融循环作用下混凝土材料寿命评估方法

严佳川，邹超英

(哈尔滨工业大学土木工程学院，150090哈尔滨，jiachuanyan@163.com)

近半个世纪以来，国内外大量混凝土结构工程出现了因耐久性不足而过早失效甚至彻底损坏的现象，耐久性问题成为全世界工程界普遍关注的研究热点［1-2］.对于全球面积广阔的寒冷地区而言，冻融循环作用无疑是引起这些区域混凝土结构耐久性下降的主要因素，直接将影响到服役结构的安全使用，混凝土结构在冻融环境下的安全性问题亟待解决.迄今为止，各国学者针对冻融作用下混凝土损伤机理开展了大量的理论和试验研究，提出了静水压假说和和渗透压假说［3-6］等混凝土抗冻机理假说，这些假说很大程度上指导并推动了混凝土材料抗冻耐久性的研究.同时基于材料学和结构工程领域的大量试验，混凝土在冻融循环作用下材料性能的衰减特点和力学性能退化规律的研究也取得了较为丰富的成果［7-13］.然而，以往的研究多集中于混凝土在冻融循环作用下材料和力学基本性能衰减规律上，而为了保证混凝土材料在冻融循环作用下的安全性，需要在冻融循环作用下，判断混凝土能否在设计基准期内完成预定的使用功能，对混凝土材料的寿命进行评估.

本文利用冻融循环作用下混凝土的力学性能试验结果，从混凝土材料本身的特点出发，依据材料学寿命准则对服役混凝土材料进行了寿命预测.分析了基于概率论和损伤理论的混凝土冻融损伤模型的适用性，同时对于国内外的冻融试验由于各自特有的针对性引起的试验结果和建立的计算模型适用范围有限的现状，建立了混凝土等效冻融损伤模型，将各混凝土冻融循环试验的结果统一起来，可对不同制备情况、不同受力状态和不同使用地区的混凝土材料寿命进行预测.

1 概述

从材料角度出发，可以用标准冻融条件下相对动弹模的损失率和质量损失率为指标进行描述，材料学的观点认为，当冻融造成混凝土相对动弹模损失率达40%时，或质量损失率达5%时，即认为混凝土已破坏.并且由文献［1-2］的试验可知，几组试件的相对动弹性模量损失率达到40%时，质量损失率均未达5%，因此，用相对动弹性模量表征混凝土的抗冻性更为准确合理.

由文献［1］的试验结果可得到混凝土自然条件下的抗冻性寿命预测模型，即

2 基于概率论和损伤理论的混凝土冻融损伤模型

混凝土的冻融循环破坏多为随机性的，所以，应用概率论解决冻融循环破坏，从逻辑上显示出其必要性［14］.同时，混凝土在各种不利条件作用下的破坏过程实质上是由内外因素所决定的与时间有关的材料本身内部损伤累积的过程，可以从损伤的角度去建立时变模型并进行寿命预测.

图1为未经冻融作用以及冻融循环300次后的混凝土试件切片扫描电镜成像结果，可以看出，未冻融试件混凝土内部气孔大小适中，分布均匀.经过300次冻融循环后，气孔间出现明显的网状裂缝.造成混凝土冻融破坏的主要原因是混凝土微孔隙中的水在温度正负交互作用下，形成冰胀压力和渗透压力联合作用的疲劳应力，使混凝土产生由表及里的剥蚀破坏.

Weibull分布可以作为材料的寿命分布模型或给定寿命下的疲劳强度模型.试验证明，对于混凝土冻融循环寿命可用Weibull分布或对数正态分布描述［14-16］，本文采用两参数Weibull分布对冻融循环作用下的混凝土寿命进行分析.

图1 混凝土试件切片扫描电镜照片

假设f(N)为混凝土冻融循环寿命N的概率密度函数，则

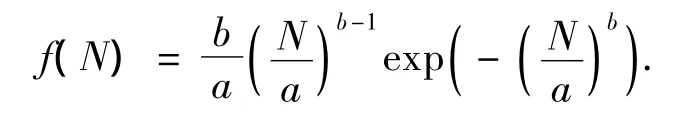
式中:a为尺度因子;b为威布尔形状因子.相应的混凝土冻融循环寿命分布函数

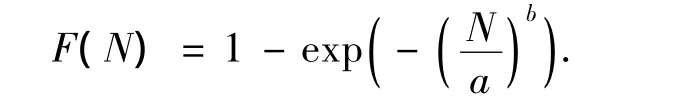
当经过n1次冻融循环后，混凝土的失效概率为

Weibull分布函数的失效概率函数是递增函数，失效概率随着抗冻混凝土冻融循环寿命N的增加而增加.混凝土材料的冻融循环寿命达到N1时，失效概率Pf(N1)=1.

由混凝土的冻融损伤失效过程可知，混凝土的损伤随冻融循环次数而逐渐累积，每一次冻融循环都将对混凝土产生损伤.

当经过n1次冻融循环后，混凝土产生的损伤为D(n1)，混凝土冻融循环寿命达到 N1时，D(N1)=1，材料失效.

对于混凝土材料，当经过n1次冻融循环后，Pf(n1)的混凝土失效，而失效的混凝土即为混凝土材料产生的损伤D(n1)，因此有［15］

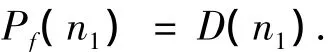
由损伤力学理论可知:

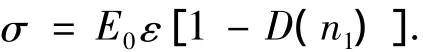
得

式中:D为损伤变量;E0(n1)、E0分别为材料冻融循环n1次后的弹性模量和初始弹性模量.

根据文献［1］的试验结果，可得

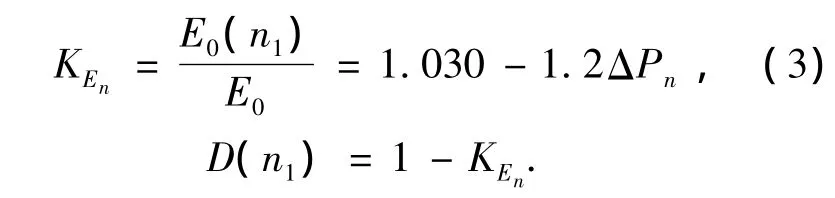
式中:KEn为经过n次冻融循环后试件的相对弹性模量;ΔPn为经过n次冻融循环后试件的相对动弹性模量损失率.

由式(3)可得

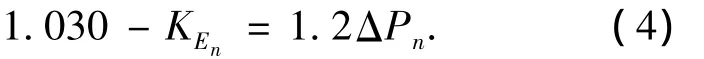
式(4)等式左侧

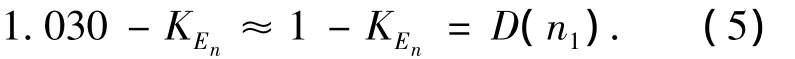
则由式(4)、(5)可得

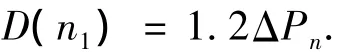
式中:ΔPn可直接通过试验测定.结合式(2)即可求解冻融循环作用下的混凝土损伤模型式

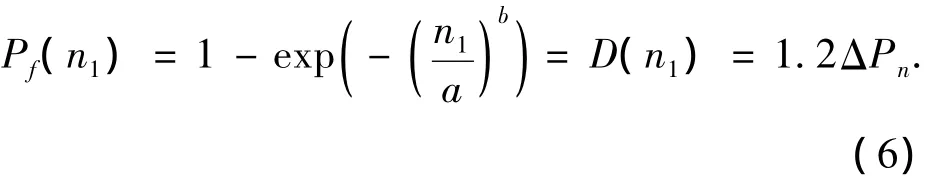
确定了混凝土n1次冻融循环后相对动弹性模量的损失率即可确定混凝土材料的失效概率函数中的参数a和b.

3 混凝土等效冻融损伤模型

文献［1-2，7］中均根据各自的试验建立了混凝土在冻融循环作用下的寿命预测模型，但由于实际环境中的混凝土一般制备条件不同，且处于多种不利因素的共同作用下，同时考虑其相互间的耦合作用来建立一个合理的寿命预测模型是非常困难的.

但是对于某一确定的条件下，冻融循环ni次产生的损伤变量可以定义为Di，对于另一个确定的条件，冻融损伤变量达到Dj时的冻融循环次数为nj，若Di=Dj，则可以在ni和nj间建立等效关系，得到nj=ne.冻融循环损伤等效示意图如图2所示.

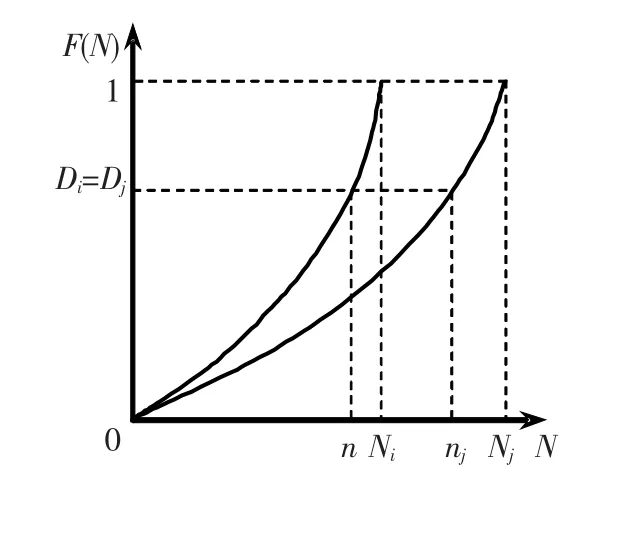
图2 冻融循环损伤等效

根据损伤变量相同原理，将某一条件下的冻融循环次数nj等效为另一条件下的冻融循环次数ne，这里称ne为等效冻融循环次数.

得

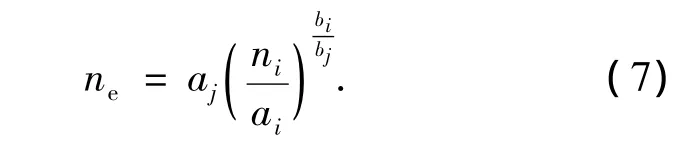
这样，即可在不同条件下得到的混凝土冻融次数间进行等效，从而对混凝土冻融循环寿命进行更加合理的预测.

4 算例

文献［1-2］中分别进行了1组和3组配合比的混凝土冻融循环试验，试件的配合比见表1、2.

表1 文献［1］混凝土配合比 kg·m-3

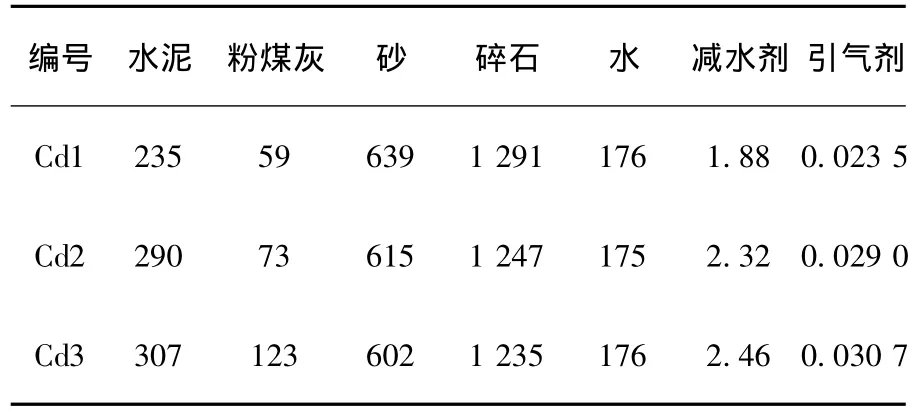
表2 文献［2］混凝土配合比 kg·m-3

文献［2］确定的冻融循环作用下混凝土寿命预测模型为

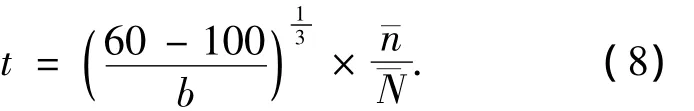
其中参数b的取值见表3.

表3 参数b［2］

利用式(8)对哈尔滨地区混凝土材料进行预测可得混凝土冻融循环寿命分别为13.5、18.95、22.48 a.而采用根据文献［1］确定的式(1)对哈尔滨地区混凝土材料进行预测，可知混凝土冻融循环寿命为30.76 a，预测结果相差很多.可见由于两试验混凝土配合比不同，导致建立的预测模型具有一定的局限性.

可以采用混凝土等效冻融损伤模型(7)，对不同冻融试验得到的混凝土冻融循环次数等效.

首先采用式(6)的冻融损伤模型对文献［1-2］中数据进行拟合，可得参数a、b的取值，见表4.基于材料学准则，当混凝土相对动弹性模量损失率达到40%时，得到哈尔滨地区混凝土冻融循环寿命见表5.从表5可知，式(6)的预测模型偏于安全.

考虑到混凝土冻融循环试验结果的离散性以及试验的不确定性，将式(6)调整为

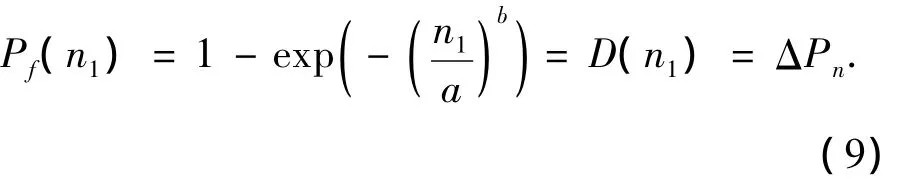
用式(9)对文献［1-2］中数据进行拟合，可得参数a、b的取值，见表4.同时，当混凝土相对动弹性模量损失率达到40%时，得到哈尔滨地区混凝土冻融循环寿命，见表5.可以看出，式(9)的预测结果与各文献中预测模型的预测结果吻合较好.因此，将式(9)作为冻融循环作用下的混凝土损伤模型.

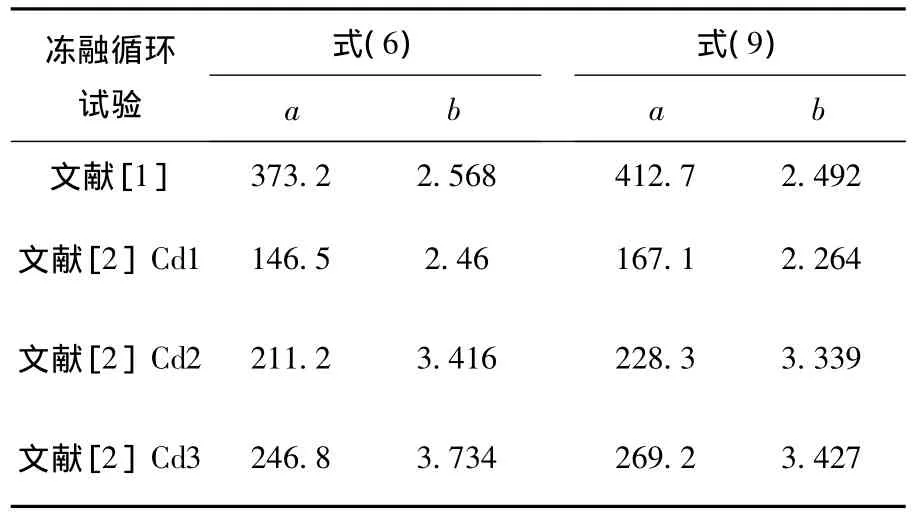
表4 参数a和b

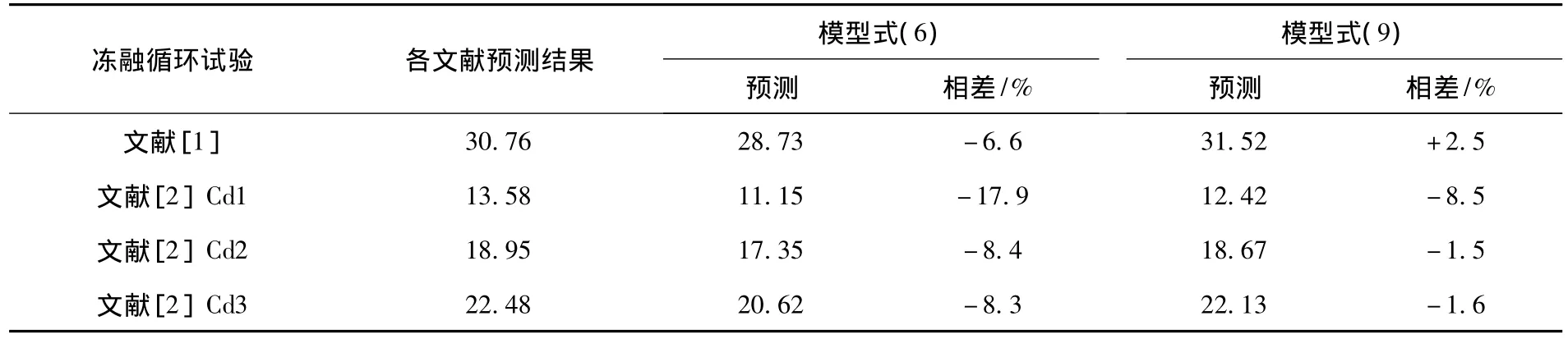
表5 哈尔滨地区混凝土冻融循环寿命的预测结果 a

其次，采用式(7)以文献［1］的冻融循环次数为标准，对文献［2］中3组不同配合比的混凝土冻融循环次数进行等效，得到的等效冻融循环次数见表6.分别以文献［2］中3组不同配合比的混凝土冻融循环次数为标准，对文献［1］中混凝土冻融循环次数进行等效，得到的等效冻融循环次数见表7.

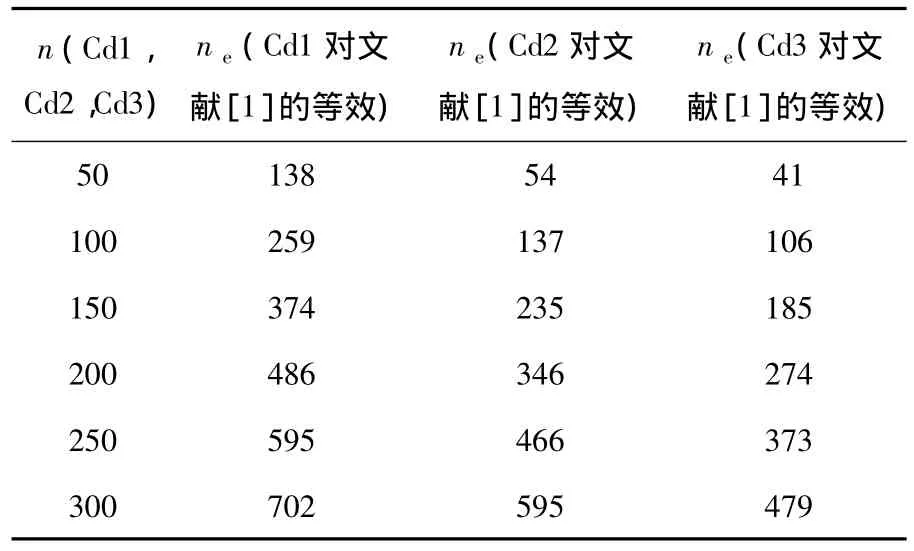
表6 等效冻融循环次数

以冻融循环作用下混凝土产生的损伤变量相同为标准，如图3(a)所示，文献［2］中配合比为Cd1的混凝土冻融循环次数为300次时，相当于文献［1］中的混凝土冻融循环次数为702次;如图3(b)所示，若文献［1］中混凝土冻融循环次数为300次时，相当于文献［2］中的配合比为Cd1的混凝土冻融循环次数为118次.

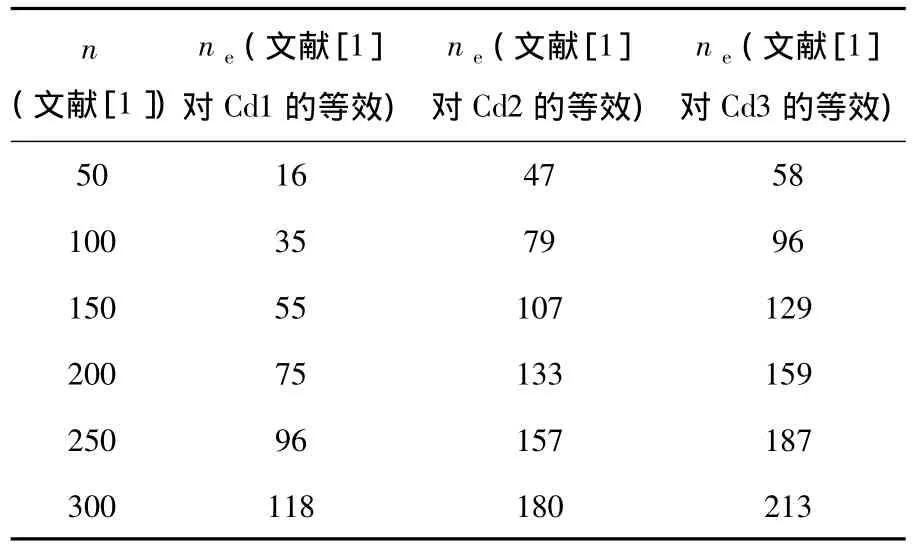
表7 等效冻融循环次数

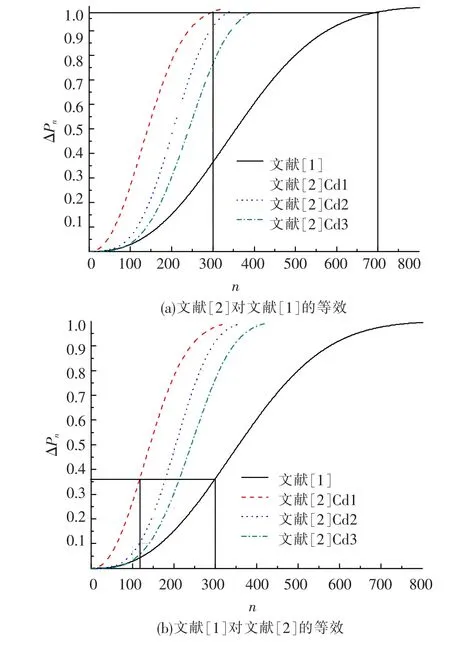
图3 等效冻融循环次数

以上即在不同试验得到的混凝土冻融次数间建立了等效关系.

5 结论

1)得到了基于概率论和损伤理论的混凝土冻融损伤模型，推导出了两参数Weibull分布的概率分布函数和相对动弹性模量损失率的关系，采用此冻融损伤模型得到的预测结果与各文献中预测模型的预测结果吻合较好.

2)建立了混凝土等效冻融损伤模型，可以将不同混凝土冻融循环试验的结果统一起来.

［1］邹超英，赵娟，梁锋，等.冻融作用后混凝土力学性能的衰减规律［J］.建筑结构学报，2008，29(1): 117-123.

［2］吴中如.重大水工混凝土结构病害检测和健康诊断［M］.北京:高等教育出版社，2005:37-42.

［3］POWERS T C.A working hypothesis for further studies of frost resistance of concrete［J］.Journal of ACI，1945，16(4):245-272.

［4］POWERS T C，HELMUTH R A.Theory of volume change in hardened portland cement paste during freezing proceedings［M］.［S.l.］:Highway Research Board，1953:137-152.

［5］POWERS T C.Freezing effects in concrete durability of concrete［M］.［S.l.］:Special Publication SP-47 (ACI)，1975:112-123.

［6］NEVILLE A M.Properties of concrete［M］.［S.l.］: Pitman Publishing Ltd，1995:123-132.

［7］李金玉，邓正刚，曹建国，等.混凝土抗冻性的定量化设计:重点工程混凝土耐久性研究与工程应用［M］.北京:中国建材工业出版社，2001:77-84.

［8］SATO Y，MUTTAQIN H，DAI Jianguo，et al.Mechanical behavior of concrete and rc members damaged by freezing-thawing action［C］//Proceedings of an International Workshop on Durability of Reinforced Concrete under Combined Mechanical and Climatic Loads.Qingdao:［s.n.］，2005:275-280.

［9］SETZER M J.Mechanisms of frost action［C］//Proceedings of an International Workshop on Durability of Reinforced Concrete under Combined Mechanical and Climatic Loads.Qingdao:［s.n.］，2005:263-274.

［10］JACOBSEN S.Calculating liquid transport into highperformance concrete during wet freeze-thaw［J］.Cement and Concrete Research，2005，35:213-219.

［11］BASHEER L，BASHEER P A M，LONG A E.Influence of coarse aggregate on the permeation durability and the microstructure characteristics of ordinary proland cement concrete［J］.Construction and Building Materials，2005，19:682-690.

［12］LI Zongjin，CHAU C K，ZHOU Xiangming.Accelerated assessment and fuzzy evaluation of concrete durability［J］.Journal of Materials in Civil Engineering，2005(5/6):257-263.

［13］DU Lianxiang，FOLLIARD K J.Mechanisms of air entraiment in concrete［J］.Cement and Concrete Research，2005，35:1463-1471.

［14］李田，刘西拉.混凝土结构耐久性分析与设计［M］.北京:科学出版社，1999:134-165.

［15］刘远.基于损伤理论的混凝土抗冻耐久性随机预测方法研究［D］.杭州:浙江大学建筑工程学院，2006.

［16］宋玉普，冀晓东.混凝土冻融损伤可靠度分析及剩余寿命预测［J］.水利学报，2006，37(3):259-263.