硅锗超晶格结构热导率的分子动力学模拟

孙兆伟，张兴丽

(哈尔滨工业大学卫星工程技术研究所，150001哈尔滨，sunzhaowei@sina.vip.com)

超晶格材料具有良好的热电性质，在计算机芯片、MEMS、纳米材料制造、航空航天等领域有广泛的应用.由于在很多情况下，热问题一直是这些技术发展的瓶颈问题，因此超晶格结构热物性已成为热传导领域的1个新的研究热点.分子动力学计算机模拟是研究微尺度材料热传输特性的有力工具，特别是对于一些理论上难以说明或实验中难以观察的现象给出基于物质微观结构及分子动力学关系的解释.从统计物理的角度可以将分子动力学分为平衡分子动力学模拟(EMD)和非平衡分子动力学模拟(NEMD).前者计算平衡系统的热流与时间的相关函数，然后通过Green-Kubo关系式得到热导率;后者需要对系统施加能量产生热流，得到系统的温度梯度，根据Fourier定律计算热导率.近年来，许多学者通过分子动力学方法对超晶格材料的热导率进行了深入的研究.Chen等［1］利用NEMD模拟方法研究了晶格周期长度对超晶格结构热导率的影响，得出当晶格的周期长度小于声子的平均自由程时，热导率会出现最小值的结果;Deyu等［2］对Si/SiGe纳米线结构进行研究，表明其热导率受边界散射机制的影响随着温度的升高而有下降的趋势.这些研究都表明微尺度下超晶格结构的热导率明显小于大体积情况下的热导率值.本文在此研究的基础上利用NEMD模拟方法研究了Si/Ge超晶格结构热导率随周期长度、周期数及温度的变化规律，并且讨论了界面热阻对超晶格结构热导率的影响特性.

1 分子动力学模拟方法

1.1 超晶格结构导热模型

超晶格结构导热模型如图1所示.在Y、Z方向施加周期性边界条件时，由于垂直热流方向的横截面积过小会对热导率的计算结果产生误差［3-4］，因此本文选取的YOZ横截面积为4 UC× 4 UC(Unit Cell，晶胞长度).为建立热流方向的温度梯度，在X方向上布置随机恒温热墙.模型中的高低温热墙材料同各自临近的超晶格材料相同，并设定其厚度为3 UC;模型最外层设置厚度为2 UC的绝热壁，作用是减少导热层内的粒子蒸发，防止与外界产生热量交换，并设定该区域粒子的速度为0.

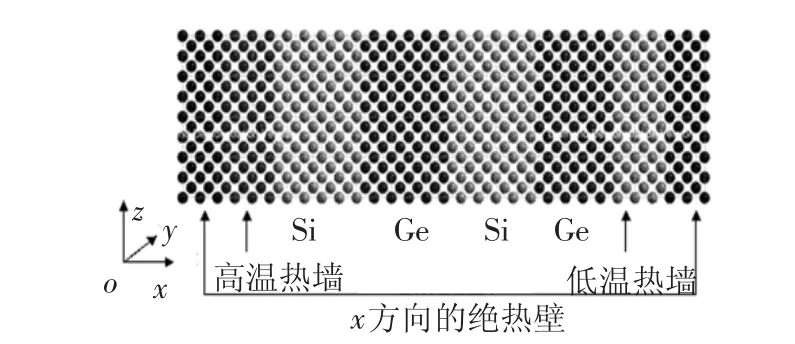
图1 硅锗超晶格结构非平衡分子动力学模拟模型

1.2 作用势能模型

Stillinger和Weber在1985年提出了稳定金刚石结构的多体势能函数来描述超晶格结构分子之间的相互作用，N个粒子的总势能为［5］

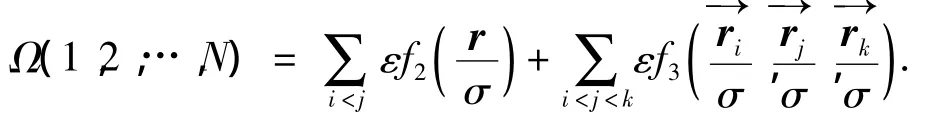
上式中两体、三体作用式分别用下列公式表达:

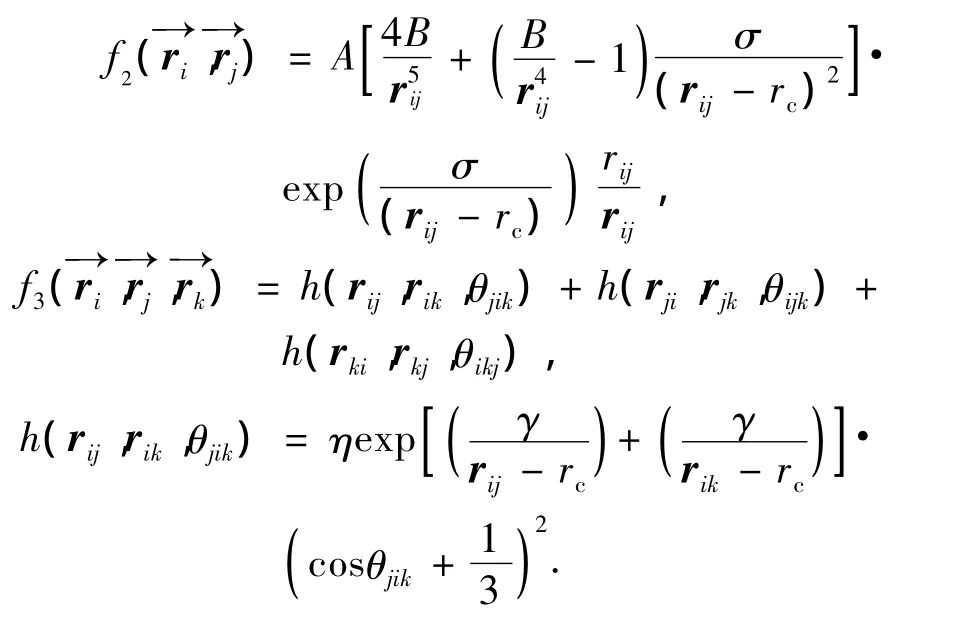
其中θjik是rij和rik的夹角，式中的各物理参数值如表1所示［6］.

表1 硅锗S－W势能参数

计算分子间作用势能和作用力需要花费大量的运算时间，因此本文采用Cell列表法为Velet列表法建立列表，用Velet列表法计算原子间势能和作用力，这样可以大大提高计算速度［7］.

1.3 局域温度修正

由Boltzmann分布函数可以获得导热区域内每个粒子的动能，系统温度可以表示为

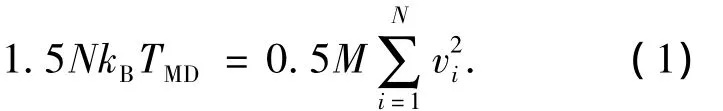
式中，kB是Boltzmann常数，N为系统中的粒子数.

式(1)成立的前提条件之一是系统温度远高于材料的debye温度θD，由于模拟过程中的平衡温度低于Si的Debye温度(645 K)，因此需对系统的局域稳定进行量子化修正，才能获得超晶格结构热导率的真实值［8］.假设系统总能量是动能的2倍，通过求解积分方程得到系统的真实温度，如下所示:

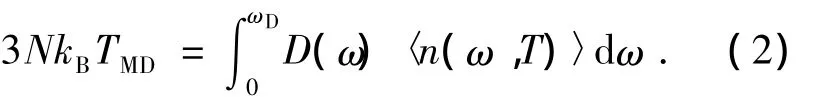
式的右边是系统中粒子的总能量，D(ω)为声子密度分布函数;ω为声子频率;n为对应于热平衡温度T的声子平均占有数，该占有数满足Planck分布(即Bose-Einstein统计).

这样Fourier定律中的温度梯度可以修正为

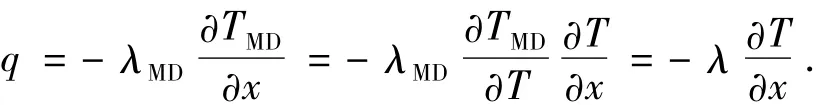
1.4 热导率计算

利用非平衡分子动力学(NEMD)方法，对系统施加1个给定的热流，在系统内部自然形成1个温度梯度.系统的热流通过动能的变化量反应，X方向的热流密度可以表示为

由Fourier定律得到热导率为

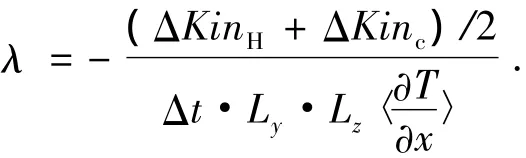
其中:ΔKinH、ΔKinc分别是高温端和低温端在时间Δt内的动能变化;Ly·Lz为截面YOZ的面积;Δt为时间步长，Δt=0.005τ0(τ0为特征时间，且

2 模拟结果

2.1 导热区域的温度分布

本次对Si/Ge超晶格结构的NEMD模拟总的模拟步长数为7×107，其中前106步使系统趋于平衡.在不同的温度下，高低温热墙的温度设为Thot=(T+20)K及Tcold=(T-20)K.根据式(2)得到周期长度为10 UC，周期数为2的超晶格结构X方向导热层的温度分布，如图2所示.

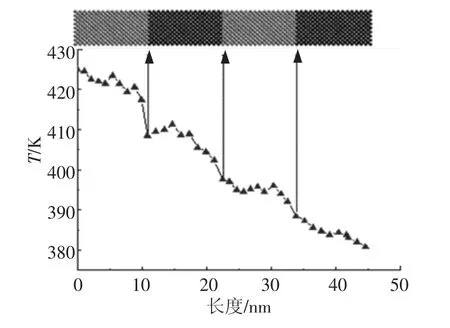
图2 界面温度的变化

从图中可以看出在Si-Ge每个交界面处都存在温度跳跃，在温度较高的第1个界面处的突变要比温度较低处更加明显.超晶格结构界面处平衡温度的主要影响因素是:1)高温热墙与其临近的Si粒子层和低温热墙与其临近的Ge粒子层之间的界面特性;2)高低温热墙的厚度.由于随着界面周期数的增加，高低温热墙厚度对导热层温度的影响逐渐减弱［9］，因此本文中的温度跳跃变化主要是受界面热阻机制的影响，即靠近高温热墙处粒子的界面反射率增加使界面热阻增加，从而引起温度的下降［10］.另外Si和Ge粒子通过第1个界面的声子振动波谱是连续，而在剩余的界面声子振动波谱的连续性降低，这也导致第1个界面温度下降得比其余界面更加明显［11］.

2.2 周期长度对超晶格结构热导率的影响

通过改变超晶格结构的周期长度来研究周期长度与热导率之间的变化关系，如图3所示.随着周期长度的增加，在系统温度为300 K和500 K时热导率也随之增大，并且两者接近于线性关系.

超晶格结构的热阻由两层材料的固有热阻和界面热阻组成，因此本文结构的热阻表达式为

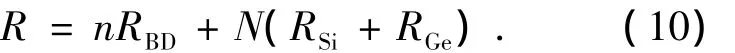
式中的RBD为界面热阻;RSi、RGe为硅锗材料每层的热阻，可近似为常数;n为界面层数，其值为n= 2N-1，N为超晶格的周期数.Chen等［10］通过理论公式推导得出固体超晶格结构有效热导率表达式为

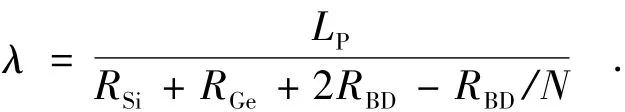
式中LP为超晶格结构的周期长度.上式说明超晶格结构的热导率随着周期长度的增大而增大，并且两者呈线性关系，与本次的模拟结果吻合较好.

图3 热导率同周期长度的关系

2.3 周期数对超晶格结构热导率的影响

超晶格结构中，周期数的变化也会使界面热效应发生改变，从而导致热导率发生变化.图4是温度为400 K时，周期长度分别为5 UC、10 UC的结构热导率随周期数的变化关系.从图中可以很明显看出2种结构的热导率随周期数的增加而增大，并且周期长度越大的结构，其周期数对热导率的影响越明显.这是因为周期数越大，Si/Ge交界面就越多，界面总热阻随之增加;同时周期数越大，也使导热层总厚度增大，因此界面热阻在总热阻中所占的比例不断下降，界面效应慢慢减弱，热导率就逐渐增大.对于周期长度更大的结构，整个导热层厚度的增加使温度梯度下降更加剧烈，热导率上升更快.

2.4 温度对超晶格结构热导率的影响

图5是周期长度为10 UC的Si/Ge超晶格结构温度与热导率的变化关系，从图中可以看出热导率随着温度的升高而略微增大.由于温度越高引起的热流波动越大，使振动频率大的声子比振动频率低的声子要多，从而增加了粒子在界面处的非弹性散射几率，界面热阻变小，热导率也随之逐渐增大.与文献［12］中的相应的SiGe合金结构相比，超晶格结构可以有效的减小材料热导率，从而提高材料的热电品质指数.

图4 热导率同周期数的关系

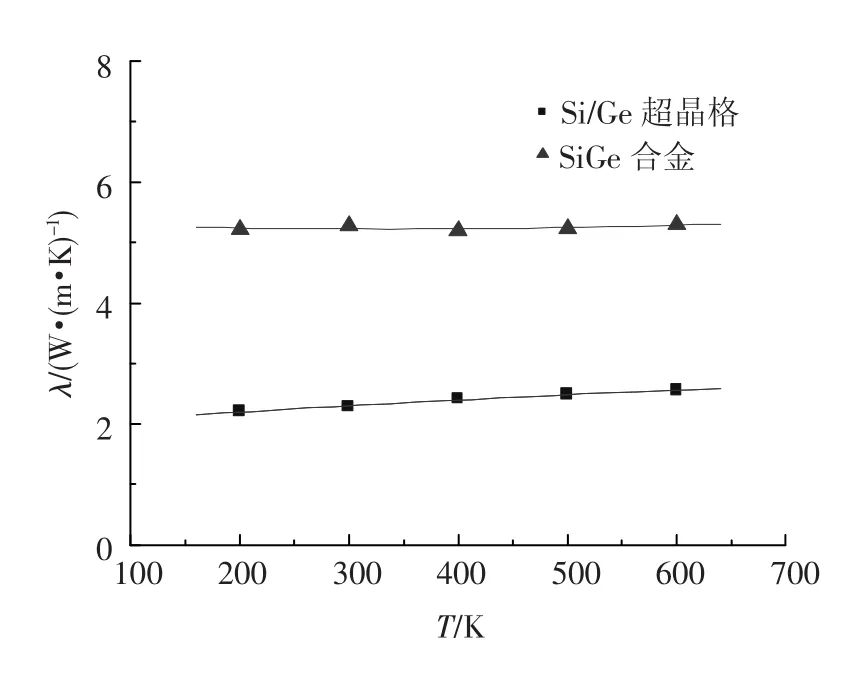
图5 热导率同温度的变化关系

3 结论

利用非平衡分子动力学方法分析了硅锗超晶格结构的热传导性能，仿真结果表明:

1)温度在靠近高温热墙的第1个交界面发生明显突变，这种现象应归结于界面几何特性的不同，导致声子反射率不同.第1个交界面的反射率增加，界面热阻因此增加，使温度发生跳跃.

2)超晶格结构的法向热导率随着周期长度及周期数的增加都呈近似线性地增加.周期长度越大的结构，周期数对热导率产生的影响越大.界面热阻效应随着周期数的增加而慢慢减弱.

3)随着温度的升高Si/Ge超晶格结构的热导率也随之略微增大，这与高温下分子的界面散射机制有关，同时模拟结果明显小于相应的合金结构热导率.

［1］CHEN Yunfei，DEYU L，JENNIFER R.Minimum superlattice thermal conductivity from molecular dynamics［J］.Physical Review B，2005，72(174302):1-6.

［2］DEYU L，YIYING W，ARUN M.Thermal conductivity of Si/SiGe superlattice nanowires［J］.Applied Physics Letters，2003，15(83):3186-3188.

［3］孔宪仁，吴国强，孙兆伟，等.单晶碳和锗薄膜热导率的分子动力学模拟［J］.哈尔滨工业大学学报(自然科学版)，2006，38(4):517-519.

［4］SCHELLING P K，PHILLPOT S R，KEBLINSKI P. Comparison of atomic-level simulation methods for computing thermal conductivity［J］.Physical Review B，2002，65(14):144306.

［5］STILLINGER F，WEBER T.Computer simulation of local order in condensed phases of silicon［J］.Physical Review B，1985，31(8):5262-5271.

［6］SRINIVASAN S，MILLER R S.On parallel nonequilibrium molecular dynamics simulations of heat conduction in heterogeneous materials with three-body potentials: Si/Ge superlattice［J］.Numerical Heat Transfer B，2007，52(4):297-321.

［7］弗兰克.分子模拟——从算法到应用［M］.汪文川，译.北京:化学工业出版社，2002:351-354.

［8］吴国强，孔宪仁，孙兆伟，等.单晶硅薄膜法向热导率的分子动力学模拟［J］.哈尔滨工业大学学报(自然科学版)，2007，39(9):1366-1369.

［9］LANDRY E S，MCGAUHEY A，HUSSEIN M.Molecular dynamics prediction of the thermal conductivity of Si/ Ge superlattices［C］//Proceedings of the HT2007 ASME-JSME Thermal Engineering Summer Heat Transfer.Vancouver:［s.n.］，2007:664-671.

［10］CHEN Yunfei，LI D，YANG J.Molecular dynamics simulation of Ar/Kr superlattice nanowires［J］.Physical Review B，2004，349(1/2/3/4):270-280.

［11］SAMVEDI V，TOMAR V.The role of interface thermal boundary resistance in the overall thermal conductivity of Si/Ge multilayered structures［J］.Nanotechnology. 2009，20(36):365701.

［12］ASHTON S，PATRICK K.Thermal resistivity of Si-Ge alloys by molecular dynamic simulation［J］.Journal of Applied Physics，2008，103(11):1-6.