一种地磁导航中的低频电磁干扰场分离方法

寇义民，夏红伟，刘 睿，王常虹

(哈尔滨工业大学空间控制与惯性技术研究中心，150080哈尔滨，kouyimin@126.com)

地磁场的精确测量是实现地磁导航的先决条件.由于地磁场的微弱性，提高测量传感器的灵敏度，以及克服来源于载体自身的磁场干扰是决定测量精度的两大核心因素.随着科学技术的快速发展，超高灵敏度的新型磁场测量设备的相继问世，及传统的磁测仪器测量精度的不断提高［1］，使得磁场传感器的灵敏度已经不再是阻碍地磁场测量精度提高的主要瓶颈，因此，如何克服来源于载体自身的磁场干扰将是提高地磁场测量精度的关键.

载体自身的干扰磁场按照其特性可以分为两类:第一类是与载体运动姿态无关的干扰场，这类干扰除了载体的部件材料被磁化而产生的恒磁干扰之外，通常来自机载的各种电器设备，如无线电设备、电源及输电线路、电机、数字开关电路等;第二类是与载体运动姿态相关的磁场干扰，包括载体中的软磁材料被地磁场磁化而产生的激磁干扰，载体在地磁场中运动而产生的涡流磁场干扰等.其中，第二类干扰可以由航磁补偿技术解决，即通过求解TOLLES-LAWSON方程来获取与姿态有关的各类干扰磁场的相关比例系数，进而根据当前载体姿态对干扰场进行估计［2-3］.目前航磁补偿技术已经非常成熟，并出现了许多系列化产品，例如加拿大RMS公司生产的AADC-Ⅱ型航空磁自动数字补偿仪，可将第二类干扰的影响降低至0.035～0.08 nT(补偿后标差)［4］.而对于第一类干扰，目前所能采取的技术手段主要有两种，即磁屏蔽技术和带通滤波器技术.然而，前者虽可大幅削弱干扰场强，却难以完全消除其影响［5］;而后者对于频率范围与地磁场相近的干扰磁场则无能为力.如何进一步清除传统技术手段层层过滤下的“漏网之鱼”，也就是强度和频率都与地磁场信号相近的低频、弱磁干扰磁场，将是本文研究的重点.

独立特征量分析法(Independent Component Analysis，简称ICA)可有效的对线性叠加的独立信号进行波形分离［6-11］，并被广泛应用到了图像与声音等信号的处理当中.但由于磁场为矢量场，干扰场的幅值与方向都具有时变特性，它们的叠加并非简单的线性叠加，故不能将线性ICA方法直接应用于磁场测量信号的分离.针对这个问题，本文提出了全新的解决方案.该方案首先对产生干扰磁场的电路的各个支路各自产生的磁场特性进行了分析，进而将各个支路进行分组，每组支路各自看做是1个独立干扰源，从而使得每个干扰源都产生相对载体方向固定的干扰场，解决了干扰场方向时变的问题.同时，对载体的姿态提出要求，最终以增加干扰源数目为代价，将各种磁场的叠加由总幅值的非线性叠加，化简成为在传感器敏感轴方向上的线性叠加，从而满足了线性ICA的应用前提.最后，提出使用相关系数的绝对值对分离后的信号波形与地磁图进行匹配的方法，从而有效克服了ICA自身的模糊性缺陷.

1 ICA方法在磁场信号分离中遇到的困难

1.1 ICA方法简介

已知有若干个相互独立的信号源，彼此发出互不相关的波形信号.采用几个独立探测器来检测信号输出，由于探测器放置位置距离的不同，每个探测器所检测到的信号波形都是原始n个信号以不同组分比例的线性叠加.检测信号与源信号有如下关系:

式中观测向量x代表各传感器上的信号输出，向量s代表信号源输出，定常矩阵A代表两者之间的线性转换关系，可称为混叠矩阵.在工程实践中，通常只能通过传感器输出获得观测量x，而无法直接获得信号源输出s与混叠矩阵A.ICA方法将利用信号源之间相互独立的特性和概率统计学的理论，来分离出各个信号源的输出波形.

由概率论中的中心极限定理可知，多个非高斯独立随机信号的线性叠加将比其中任意一路信号更趋近于高斯分布.根据这一理论，寻找合适的线性变换对观测向量x进行处理，使得结果向量z中各个元素对应的信号所具有的非高斯性都达到最大时，每个分离出来的信号也就最接近原始的单个信号.

实际操作中，ICA的求解过程通常包含以下3个步骤:1)对混合信号的预处理，包括中心化，白化.2)选择或定义非高斯性(独立性)的度量，建立目标函数.3)利用某种最优化方法来令目标函数达到极值，从而推导出一种学习方法.常用的代价函数有峰度、微熵、负熵、互信息等.

传统线性ICA方法中，为确保各个信号源的输出可被有效分离，通常有以下假设约束必须被满足:1)各个信号源的输出必须彼此相互独立，这是ICA能够实现的最基本要求.2)最多只能有1个信号源的输出为高斯分布，多个高斯信号的混叠无法被分离.3)通常要求传感器的数目等于信号源的数目，也就是令A为满秩方阵.

除以上约束外，ICA方法还具有如下含混性:

1)ICA只能分析出各个信号源的输出波形，而无法分析出其对应幅值.这是因为，针对在仅仅已知测量值的情况下，对原始信号输出幅值乘入1个因子的同时，对系数矩阵相应的列元素除以这个因子，测量结果不变，即换句话说，si/ki可能取代si作为分离后的信号波形结果.

2)分离出的波形结果是乱序的，也就是无法与原始信号源在顺序上一一对应.这是因为在仅仅已知x的情况下，可以在式(1)中插入任意的置换阵及其逆矩阵，也就是x=AP-1Ps.这里P为单位阵交换了两行后的矩阵，如果最终将AP-1作为解得的线性转换关系，同时将Ps作为分离后的波形结果，那么将产生乱序的情况.

ICA的具体实现算法很多，有信息最大化法，基于极大似然估计的ICA方法，负熵最大化法，EASI算法，快速固定点算法(FPICA)等，具体请参阅文献［6］，在此不再赘述.

1.2 ICA在地磁导航信号处理中的问题

ICA方法在磁场信号分离与地磁导航中的主要困难有以下2个方面:

1)线性化叠加约束难以满足，而非线性ICA又难以应用.

为了简化研究问题，这里假定载体内只存在唯一低频干扰源，其在载体内各点产生的干扰磁场的强度和方向与相对位置有关.为了将干扰信号与地磁场信号分离，根据ICA的原理，需采用2个分开布置的传感器.由毕奥 -萨伐尔定律，干扰源在2个传感器所处位置上的干扰磁场可分别记为k1δH和k2δH(k1和k2是和距离平方成反比的系数，而δH与干扰源的电流强度成正比)，而地磁场在载体内部处处相同，记为H.两个位置上干扰磁场与地磁场的夹角分别记为θ1和θ2.则由矢量叠加原理和余弦定理，2个传感器所测得的总磁场强度分别为

显然干扰场信号与地磁场信号在传感器上的叠加属于非线性叠加，不可能写成方程(1)的形式，故线性ICA方法难以被直接应用.那么是否可以应用非线性ICA来解决呢?答案是依然很困难.这是因为测量值作为非线性函数时，其参数不仅包含H与δH，还包含角度值θ1和θ2.而这2个角度值也可能是时变的，且互相没有明显关联，只能各自看成独立信号.这样传感器的数目将小于信号源的数目，从而引发新的问题.

2)ICA的含混性对地磁场信号的精确匹配产生障碍.这主要包括以下两点:1)分离后的信号波形中哪个是地磁场信号波形，哪个是杂波干扰的波形;2)即使正确建立了波形信号间的对应关系，由于幅值不确定性，在其幅值发生变化的基础上，如何与原始地磁图进行匹配.

2 解决方案的论证与推导

2.1 各场源信号的线性化叠加模型的建立

为了避免求取总磁场的幅值，引入传感器敏感轴的概念，一旦敏感轴方向确定，磁场测量值为各磁场信号向敏感轴投影后的叠加值.若两传感器的敏感轴与地磁场方向和干扰场方向的夹角分别为α1(t)和β1(t)，α2(t)和β2(t)，则有

此时地磁场信号与干扰场的信号满足了线性化叠加，但是系数阵看上去却是时变的.根据ICA的前提条件，各个独立信号在传感器上的输出比例组分须是固定的，即比例系数M1= cos α1(t)/cosα2(t)和 M2= k1cos β1(t)/ k2cos β2(t)须为时不变的固定值.这里假定β1(t)=β2(t)+γ(t)，代入三角函数有

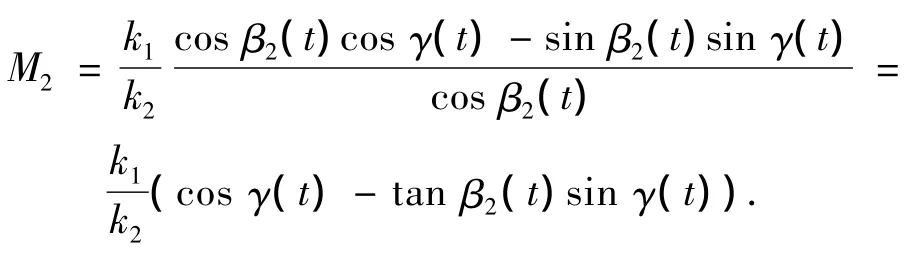
显然除非保证β2(t)和γ(t)都为时不变的值，否则很难保证M2为固定值，这就要求干扰磁场的方向在各个传感器的位置处是确定的.M1也与此类似，即只有地磁场方向在载体坐标系内保持不变才能保证M1具有非时变特性.

下面研究干扰磁场矢量相对于载体的方向问题.首先来考虑最简单的串联电路.根据毕奥-萨伐尔定律，在t时刻，微小电流源在空间中任意一固定点P产生的磁场矢量为

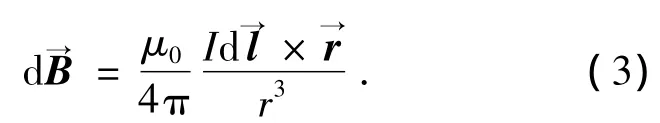
其中，μ0为真空磁导率为由电流源到P点处的矢径，I为电流强度为导线微元所对应的矢量，进一步展开，可得磁场的幅值为

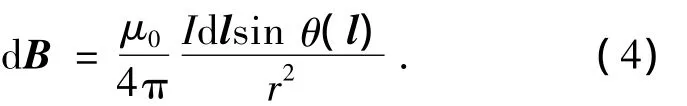
式中θ(l)为在l处导线微元dl与r的夹角，dB的方向由右手定则确定.取串联电路上的任意n个点处的电流微元，它们在P点处所形成的总磁场为

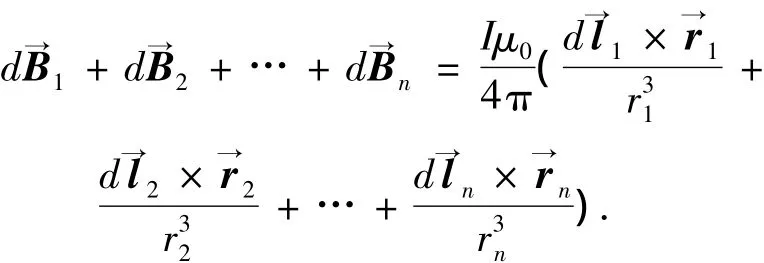
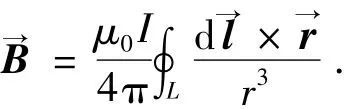
显然也是1个具有上述性质的矢量.

对于更复杂的含有n个支路的电路(并联或网状)，在只含有1个电源的情况下，利用式(3)分别求取t时刻所有n个支路在P点处的总磁场，进行叠加有

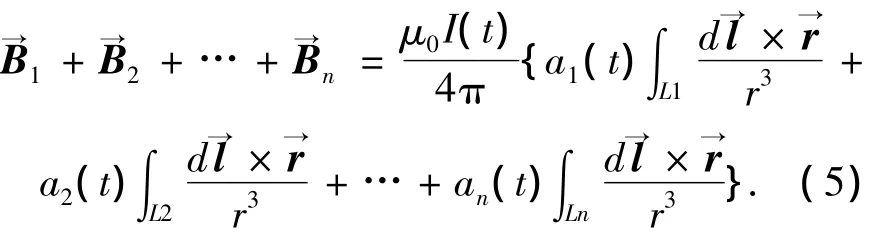
这里I(t)为电源输出总电流，ai(t)(i=1，2，…，n)表示各支路电流与总电流的比值.此时可分为如下几种情况分别讨论:

1)当各支路不含电感与电抗元件时，ai(t)为非时变固定值，由各支路电阻决定.根据前面证明，大括号中的各个积分项为幅值和方向固定的矢量，它们以固定系数ai(t)所进行的线性叠加仍是幅值和方向固定的矢量，仅和点P的空间相对位置有关.而括号外的系数仅与总电流强度有关.故此时电路产生的干扰磁场与串联电路产生的干扰磁场具有类似的性质，即方向的确定性.

2)当支路中含有电感或者电抗元件，且I(t)为频率较高的时变值时，式(5)中的ai(t)也将为时变值，此时该电路产生的总干扰磁场将不具备方向确定性.但由于各个支路各自产生的干扰场仍具备方向确定性，故每个支路可各自作为1个独立的且具备方向确定性的干扰源来处理.还可将彼此电流强度比值始终恒定的支路分成一组，作为1个干扰源，比如几个完全对称的并联支路.

3)当支路中含有电感或者电抗元件，且I(t)为频率很低的时变值时，电路中的电阻与电抗元件将分别近似于断路和通路而失去作用，此时电路产生的总干扰磁场仍具有近似的方向确定性.

通过以上分析可知，某些类型的电路产生的磁场干扰具有方向确定性.对于其余类型的电路，通过将其各个支路进行分组，作为独立干扰源看待，也可以使它们产生的干扰磁场各自具有方向确定性.含有多个电源的更复杂电路也可以按照前面的思路进行分析与分解.

对于地磁场进行分析就简单得多了.在同一位置，当载体姿态相对地理坐标系发生改变的时候，地磁场与传感器敏感轴的夹角也会相应发生变化，故要应用ICA，载体是不可以进行滚转、俯仰等机动运动的.同时，随着空间位置的变化，地磁场的磁倾角与磁偏角也会发生变化，它所产生的影响可以从2个方面来分析.

首先，根据IGRF2000模型计算主磁场磁偏角与磁倾角的变化趋势，可发现磁倾角与磁偏角的角度变化非常缓慢.例如，在E70N40位置，磁倾角沿纬度线方向每100 km变化0.983 9°，沿经度线方向每100 km变化0.488 5°，而磁偏角沿纬度线方向每100 km变化0.338 2°，沿经度线方向每100 km变化0.111 2°.故载体在较短的路径内保持平飞时，主磁场的方向变化是非常微小的.

其次，由于余弦函数在角度为0附近导数最小，如果在数据收集阶段，令传感器敏感轴近似平行于当地的主磁场方向，可以令主磁场的投影波形受磁倾角磁偏角变化的影响进一步减少.可以在开始进行信号收集之前，根据惯导输出的位置来估计当地磁偏角和磁倾角的值，然后根据这个值调整传感器的敏感轴方向，并在数据收集阶段始终保持敏感轴相对载体方向不变.

通过前面分析，由式(2)与(4)得在单一串联电路干扰源条件下磁场信号的线性叠加公式为

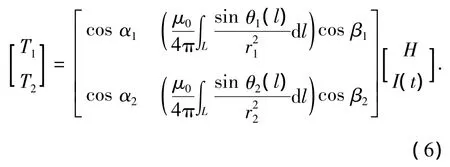
与式(6)类似，可以推出当干扰电路的n个支路被各自作为独立干扰源时(即符合第二种情况)的信号叠加模型为

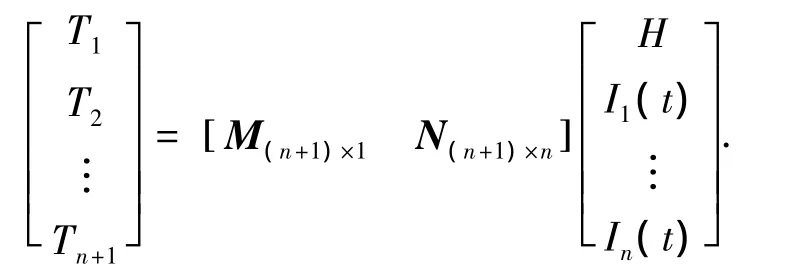
其中

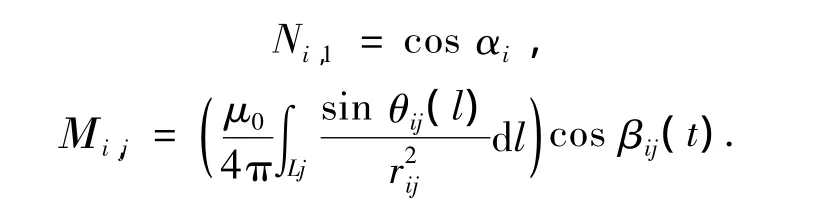
此时，总信号源个数为n+1个，角标i=1，2，…，n+1，j=1，2，…，n，αi代表地磁场与第i个传感器敏感轴的夹角，为接近0的微小量;βij为第j个干扰源产生的磁场与第i个传感器敏感轴的夹角，为固定值，由传感器与干扰源支路的空间相对位置决定;rij为第j个干扰源导线l处的导线微元与第i个传感器之间的矢径;θij(l)为第j个干扰源在l处的导线微元与rij的夹角.不同支路分组的情况下的叠加公式可由读者自行推导，受篇幅所限这里不再赘述.

2.2 克服信号分离后结果的不确定性

当ICA可以被实施之后，下一步的问题就是如何克服ICA分离出的信号的不确定性问题.由于ICA方法的含混性，有2个问题需要解决，首先由于顺序上的含混性，无法直接获知所分离出来的波形结果中哪个是地磁场的测量值，哪些是干扰磁场测量值.其次，即便解决了前一个问题，分离后的结果与实际波形之间的关系是先在幅值上乘以系数然后进行平移的关系，引入相关系数的绝对值，即

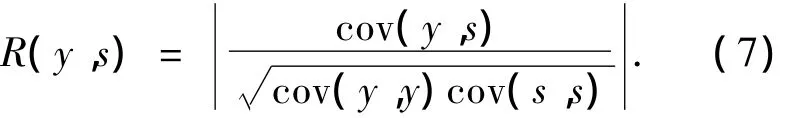
其中cov为协方差函数，R的取值位于［0，1］之间.可以证明，当y与s代表2个波形图像的幅值时，y与s在图形上越相似则R的取值越大，如果s与y为线性变换关系，R的值为1.

在没有任何关于磁场信号波形先验信息的情况下，只能用所有分离后的波形信号在惯导系统所指示的路径附近区域内进行搜索匹配，这一点与基于TERCOM的导航定位方法相似.其中能令R取最大值的路径即为载体经过的实际路径，对应的波形也就是分离后的地磁场信号波形.

2.3 信号分离与匹配的总体方案

基于前面的分析与推导，提出最终方案如下:首先要对所有电气设备干扰源进行分析，对于高频干扰源采用传统滤波器处理，对于低频干扰源，按前述方法对电路特性进行区分，获取主要干扰源的数目，并布置相应数目加1个传感器.在载体飞行过程中，按照如下步骤进行信号分离和地磁导航定位:

1)准备阶段.当发现载体的惯性导航系统输出位置明显偏离实际位置时，准备进入数据收集阶段，此时根据惯导输出位置估计当地主磁场方向，并据此调整传感器的敏感轴方向.

2)数据收集阶段.载体保持平飞，实时记录各个传感器敏感轴上的磁场信号.

3)信号分离阶段.对获得的信号采用适当的ICA方法进行波形分离.

4)搜索匹配阶段.用所有分离后的信号波形在地磁图上惯导输出路径的附近采用式(7)进行搜索匹配，能令相关系数最大的信号波形和路径即为地磁信号波形和载体的实际路径.

5)校正阶段.根据前面匹配结果，修正惯导系统累积误差，载体脱离平飞状态，可自由机动.

3 仿真与结果分析

地磁异常采用2007年7月第24届UGG大会发布的全球地磁异常图(WDMAM)中欧洲部分中地磁异常剧烈区域数据作为标准参考［12］.从磁图矩阵网格中抽取一行的一部分作为实测地磁数据.仿真中的干扰电路如图1所示.图中电路采用2 Hz的低频交流电压源，并具有3个支路，对应电流i1、i2、i3.由于含有容抗性器件，根据前面的分析，这3个支路可看作是3个独立的干扰源.数据收集阶段所经过路径上的地磁信号波形，以及3个干扰源对应的电流值如图2所示.图3为在4个磁传感器敏感轴方向上分别检测到的磁场波形，为地磁场与干扰场在敏感轴向上投影的叠加.

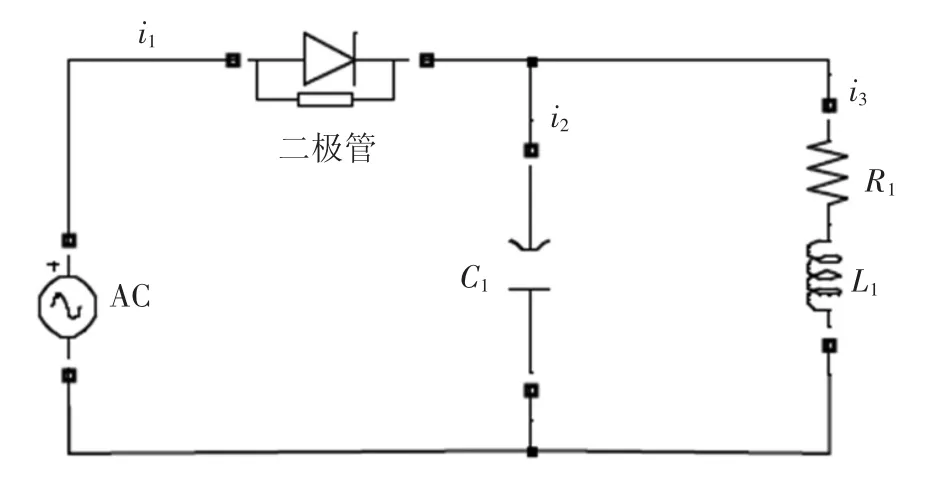
图1 仿真实验中所用到的干扰电路

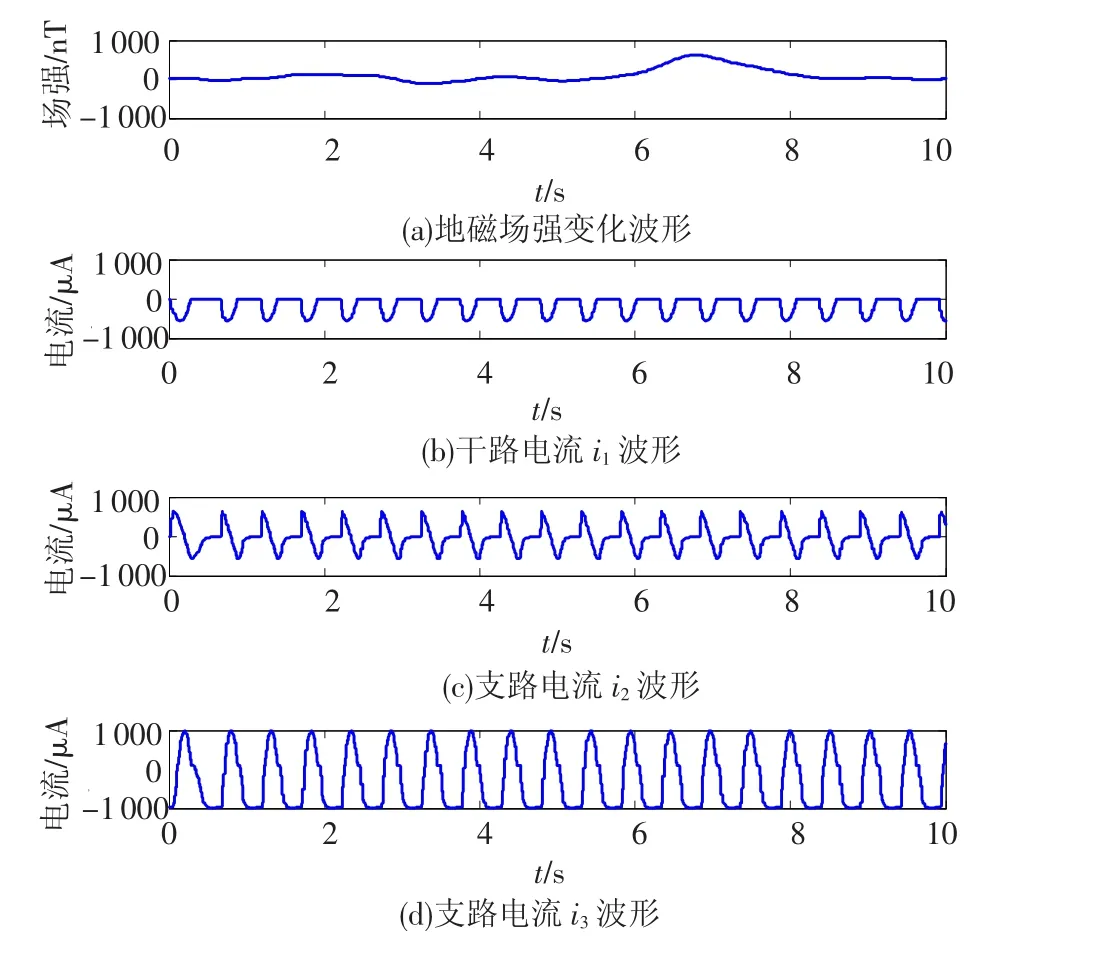
图2 实际地磁场强波形和干扰电路各支路的电流波形

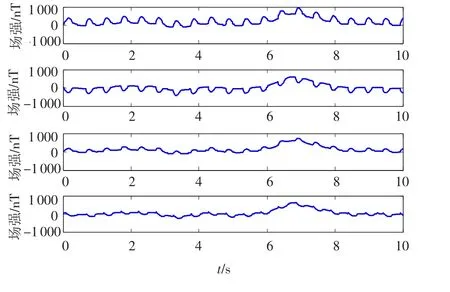
图3 在3个传感器上的混叠后信号波形

采用ICA中的定点法(FPICA)进行信号分离，为了验证其鲁棒性，加入了标差为0.1 nT的传感器测量噪声.分离后的信号波形如图4所示(由于ICA方法的幅值不确定性，图4并未给出纵坐标):

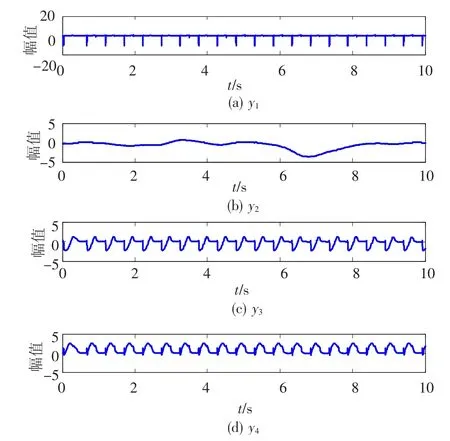
图4 分离后的信号波形

从图中可以看出，分离后的4个波形y1、y2、y3和y4虽然与原始波形幅值不同，但是在形状上保留了较大的相似度，相当于是对原始波形进行了平移、压缩、以及翻转.用肉眼观察可以发现分离后的波形信号与原始信号的对应关系，即地磁信号对应y2，i1对应y1，i2对应y3，i3对应y4.

这里需要指出的是，电流波形分离后形状上的失真度较大，而地磁信号波形分离后形状上的失真度较小.造成这种现象的原因是三路电流之间具备一定的相关性(频率相同，且干路电流i1的幅值为2个支路电流i2和i3的和)，而地磁场信号与3个电流却是完全独立的.

采用相关系数绝对值进行相关度验证.这里用H代表载体运动路径上的真实地磁信号，用分离后的4路信号波形分别与H通过式(7)计算相关度，可得

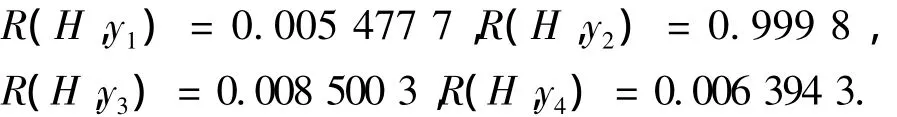
显然y2与H相似度最高.

进一步，用相似度最大法则在整个区域范围内进行匹配，匹配后的结果如图5所示，图中横线为实际路径，圆圈为匹配结果，两者吻合的非常好.

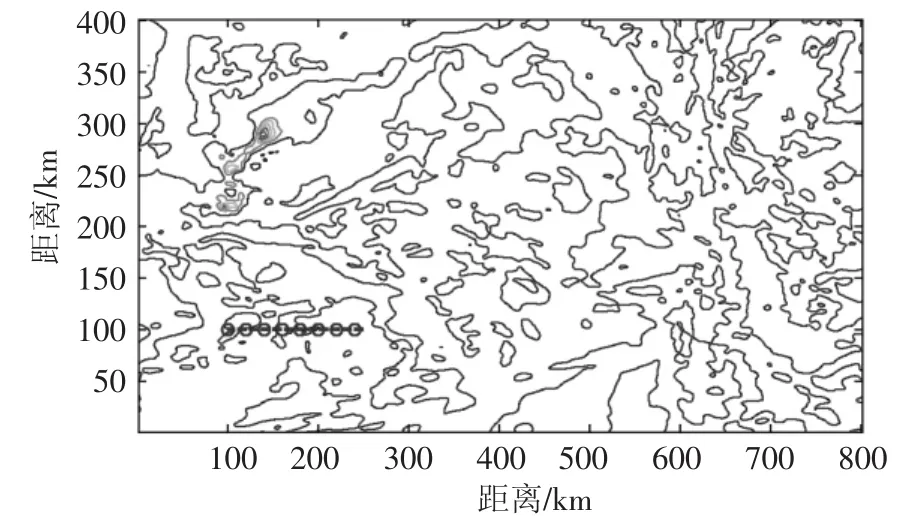
图5 相关匹配结果

4 结论

本文针对地磁导航技术提出了一种克服低频电气干扰源影响的解决方案.理论分析与仿真表明，本方案可有效克服传统ICA方法应用于地磁导航中所遇到的2个主要障碍，即线性化叠加前提无法满足，及分离后的信号存在模糊性而难以精确匹配.本文提出的电路电磁特性分析法，是本方案能够得以实施的基础和关键.但在干扰电路结构复杂，造成划分出的干扰源个数较多的情况下，可能造成计算量过大，匹配花费的时间过长的问题，这还需要在下一步的研究中进一步完善.

［1］涂有瑞.飞速发展的磁传感器［J］.传感器技术，1999，18(4):5-18.

［2］BICKEL S H.Small signal compensation of magnetic fields resulting from aircraft maneuvers［J］.Aerospace and Electronic Systems，1979，15(4):518-525.

［3］GROOM R W，JIA R，LO B.Magnetic compensation of magnetic noises related to aircraft’s maneuvers in airborne survey［J］.BHL Earth Sciences，2004，2:12-16.

［4］刘晓杰.航磁补偿技术研究［D］.长春:吉林大学，2009:5.

［5］袁雪萍，潘加明.电磁屏蔽中的难题——磁场屏蔽［J］.电子质量，2006(10):70-72.

［6］HYVARINEN A，KARHUNEN J，OJA E.Independent component analysis［M］.New York:John Wiley＆Sons，2001.

［7］张建明，林亚平.独立成分分析的研究进展［J］.系统仿真学报，2006，18(4):992-1001.

［8］CARDOSO J F.Blind signal separation:statistical principles［J］.Proceedings of IEEE，1998，86(10): 2009-2024.

［9］HYVARINEN A，OJA E.Independent component analysis:algorithms and applications［J］.Neural Networks (S0893-6080)，2000，13(4/5):411-430.

［10］杨竹青，李勇.独立成分分析方法综述［J］.自动化学报，2002，28(5):762-771.

［11］杨英华，吴英华.基于独立源分析的过程监测方法［J］.控制与决策，2006，21(10):1190-1196.

［12］KORHONEN J V，FAIRHEAD J D，HAMOUDI M，et al.Magnetic anomaly map of the world(and associated DVD)，scale:1∶50 000 000，commission for the geological.map of the world［M］.1st ed.Paris:［s.n.］，2007.