环境荷载共同作用下自升式平台地震响应分析
2011-03-12金书成杨炎华杜松
金书成,杨炎华,杜松
(中交第二航务工程局有限公司技术中心,长大桥梁建设施工技术交通行业重点实验室,湖北 武汉 430040)
0 引言
自升式海洋平台结构复杂、体积庞大、造价昂贵,特别是它所处的海洋环境十分复杂和恶劣,承受着多种随时间和空间变化的随机载荷,包括风、海浪、海流、海冰和潮汐等,同时还受到地震作用的威胁。目前对地震作用下海洋平台结构的动力反应分析还相对较少。事实上,海底与陆上一样经常发生地震。虽然地震荷载没有波浪荷载和风荷载出现的频率高,且发生时持续时间也很短,但是大的地震所造成的破坏却是非常严重的,且自升式海洋平台的事故将造成重大的经济损失、社会影响及严重的次生灾害。因此,在我国大力建设跨海通道及开发近海石油的今天,自升式海洋平台作为海洋施工的重要装备,研究地震对其的破坏作用很有必要[1]。
海洋平台的抗震分析与陆地结构物不同,不能仅仅考虑地震作用。事实上,海底地震发生时,平台结构会同时受到地震和风、海流、波浪的共同作用,且地震对平台结构的影响不仅仅是增加了结构惯性力,还将增大平台与周围水体、地基土体的耦合效应[2]。
为此,本文在考虑流体附加质量及地基土体抗转效应的前提下,建立了适合动力分析的海洋平台计算模型,并利用弹塑性时程分析方法研究了其在地震及其他环境荷载共同作用下的动力响应。
1 共同作用的运动方程
地震与环境荷载共同作用时,平台的结构运动方程为:

式中:[M]、[C]和[K]分别为平台结构的质量、阻尼、刚度矩阵;分别为平台各节点的加速度、速度和位移向量;为地震动加速度向量;{fH}为环境荷载向量[2]。
本文中风力和海流作用等效为集中力添加于相应节点,而波浪力的计算则采用莫里森方程,且考虑海水浮力和附加质量,莫里森方程如下:
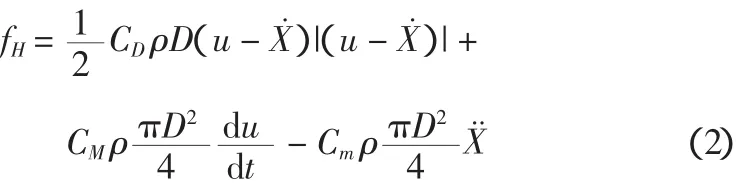
式中:CD为法向拖曳力系数;CM为惯性系数;Cm为附加质量系数;ρ为流体密度;D为圆管外径;u为流体速度;X˙和X¨分别为结构速度和加速度。
结构阻尼矩阵 [C]采用Rayleigh阻尼形式:
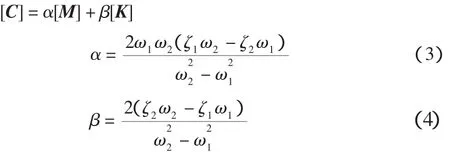
式中:ω1和ω2分别为平台的第一阶和第二阶自振圆频率;ζ1和ζ2分别为第一阶和第二阶自振圆频率所对应的阵型阻尼比。
本文运动方程的求解采用Newmark时间积分法。
2 计算模型的建立
拟建立模型的自升式海洋平台为三桩腿形式,桩腿为三角形桁架式,斜撑布置为倒K形。各桩腿独立桩靴。平台长(含桩角箱)89.0m,平台总宽80.4m,型深(舷侧)10.1m。上部平台质量约为12 000 t,桩腿总长144m,上船体高9.14m。弦杆外径1 050mm,壁厚16mm;外水平杆与斜撑外径325mm,壁厚22mm;内水平杆外径245 mm,壁厚16mm。详细建模数据参见文献[3]。
2.1 模型的简化
由于结构自由度的多少和单元的数量对动力分析的计算精度和时间有着极大的影响,而且本文主要研究的不是船体的破坏,因此本文对自升式海洋平台的动力模型进行适当简化。1)将船体视为传力结构,弦侧结构、纵向舱壁及横舱壁简化为刚性梁,即利用梁单元来代替板壳单元。2)船体部分质量通过集中力形式或增加刚性梁的材料密度方法添加[4]。
2.2 附加质量
在地震或海冰等动力作用下,处于深水中的结构会发生振动和变形,并引起周围水体的晃动,水体又以动水压力的形式反作用于结构,改变结构的振动和变形状态,这种作用与反作用伴随作用过程的始终。直径为a的圆柱体沿某一方向运动时,如沿x轴方向运动,利用流体力学知识可解得其单位长度在x方向受到的力为:

式中:ρ为水密度;a为圆柱体直径;U¨为圆球径向振动的加速度。
所以其单位长度的附加质量为:m=ρπa2,式中参数意义同式(5)。即结构在无限流体域中振动时的附连水质量由公式m=ρπa2计算,a即取为水下各杆件的外直径,附加质量均匀分布在水面下的杆件上,采用调整水中各杆件密度方法来实现。
本文在泥面下桩腿设置虚拟节点,并采用等效梁模拟地基的抗扭转约束,故不再考虑由于结构运动而带动周围土体运动引起的附加地基土质量[5-6]。
2.3 模型中边界约束的处理
1)对于船体与桩腿的连接,本文采用大刚度等效梁来模拟连接弦杆与船体之间的销子,即将梁的刚度设为无限大,以此来模拟船体对桩腿的约束作用。
2)桩腿与基础的连接以弹性约束模拟。在以往的自升式平台模型中,桩腿海底处的边界约束往往被处理为铰支约束,这种方法略去了海底基础对桩腿下端的转动约束,此时桩腿的弯矩全部集中于桩腿与船体的连接处,因此是偏于保守的。事实上海底基础对于桩腿是具有转动约束作用的,这种约束将使桩腿下端承受弯矩,从而使桩腿与船体连接处的弯矩值减少。本文根据挪威船级(DNV)规范的计算方法,考虑海底土壤与桩脚箱之间的相互作用,确定桩腿海底的约束边界。具体做法是:在海底每根桩腿截面的几何中心设虚拟节点,每根桩腿的3根弦杆通过刚性梁连接到桩腿的几何中心处的虚拟节点,几何中心的虚拟节点3个方向的位移为零,即设为铰接。土壤及桩靴的抗转约束作用,通过在铰接点施加等效抗转空间梁来实现。等效抗转空间梁的抗转刚度根据1984年挪威船级社(DNV)提出的抗转弹簧刚度计算公式计算[3]。

式中:G为土壤的剪切模数;ν为土壤的泊桑比,ν≈0.3;r0为桩脚箱的半径或接桩靴与海床接触面积的半径。
根据式(6)计算抗转弹簧刚度KS值,并根据材料力学知识确定圆截面等效梁长度L与直径D的关系,假定一个L值就可以得到提供相应抗转弹簧刚度KS的等效梁的直径D。本文取L为3m,计算得直径D为1.176m。
2.4 环境荷载添加
风荷载等效为集中力添加在船体上,作用在结构上的风荷载可以采用APIRP2A中的风力计算公式来计算:

式中:F为风力,N;V为风速,km/h;CS为形状系数;A为建筑物迎风面积,m2。
将海流简化为稳定的定常流动,也简化为集中力添加于水下桩腿各节点处。海流可按与动能成正比的阻力来计算,即:

式中:u为海流流速,其余符号与前述相同。在浅海区,流速随水深的变化规律可表示为:

式中:us为表层流速;d为水深;z为自海底以上的高度。
根据文献 [3]选择斯托克斯5阶波浪理论来计算波浪载荷。
2.5 平台主要计算指标
平台作业水深85m,气隙高度12m,正常作业状态下:风速20m/s,波高5.5m,波浪周期8 s,表面流速0.5 m/s,土壤基础弹性模量35 000 kN/m2。
利用sap2000建立计算模型,见图1。

图1 平台整体计算模型与基础约束示意图
3 算例
首先对结构进行模态分析,各环境荷载作用方向均取为y-向,得到平台的前三阶固有频率为:0.162,0.177,0.230,并计算Rayleigh阻尼。
根据模态分析结果及文献 [3]动静位移的计算结果,船宽方向的船体柔性大于船长方向,船宽方向动力放大系数大于船体长度方向的动力放大系数。本文旨在分析环境荷载与地震共同作用,故将环境荷载作用于刚度较大、动力放大系数较小的船长方向(即y向),以分析共同作用中环境荷载作用方向对平台响应的影响[3]。
本文选取ElCentro波,兰州波和一条人工波对平台进行弹塑性地震反应时程分析,分别从整体坐标系的x+,y+,y-三个方向输入,调整各地震波峰值为220 cm2/s,计算7度罕遇地震作用下结构的船体形心位移、基底剪力、基底弯矩。采用Newmark时间积分法进行时程分析,时间步长为0.02 s,考虑由于轴向压缩和风流作用引起的桩腿整体侧向位移二次力矩,即P-△效应。本文得到了各地震波在不同方向输入时,形心位移与基底剪力关系曲线(图2~图4),形心位移与对应基底弯矩的关系曲线(图5)(注:如x+向形心位移对应y轴向的基底弯矩)[8]。

图2 ElCentro波作用下的位移-剪力曲线

图3 兰州波作用下的位移-剪力曲线
本文分别计算了3个地震波从x+、y+、y-三个方向输入情况下的形心位移和基底剪力、基底弯矩的关系。限于篇幅,仅列出各项参数绝对值的最大值如表1。
计算结果表明地震波在环境荷载作用方向(y-向)输入时结构的形心位移、基底剪力最大。与x向输入时的计算结果相比,y+向与y-向输入时的形心位移、基底最大剪力、基底最大弯矩均比较大。可见即使环境荷载作用在刚度较大、动力放大系数较小的方向,算例中地震与环境荷载同向输入仍引起了结构较剧烈的响应。
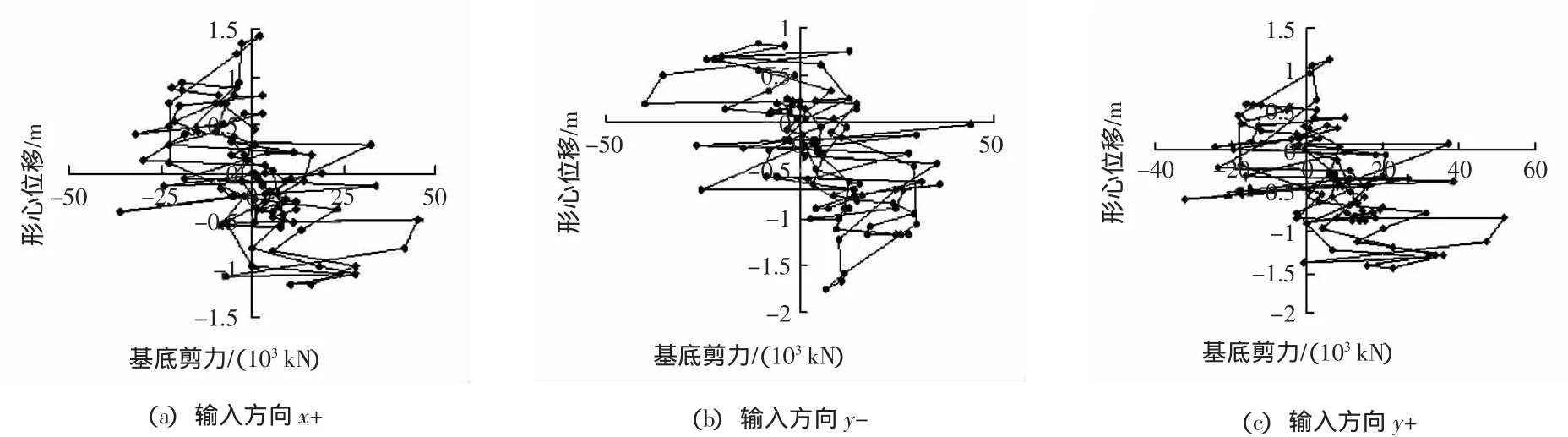
图4 人工波作用下的位移-剪力曲线

图5 x向形心位移与基底弯矩曲线

表1 计算结果汇总
4 结语
地震与其他环境荷载共同作用下的平台响应分析对研究现役自升式海洋平台的破坏有着重要意义,为在地震活跃地带进行施工作业的自升式海洋平台着底稳性分析及极限承载力计算提供了重要的计算指标和方法。
本文建立一个典型的自升式海洋平台动力计算模型,选择了3个典型的地震波分别从3个方向输入,利用弹塑性时程分析方法,计算了地震与风、浪、流等荷载共同作用下结构的各项响应,对自升式海洋平台的抗震设计和地震作用下的稳性验算有一定意义。计算结果表明环境荷载作用的方向对自升式海洋平台地震响应有重要影响,地震与环境荷载同向作用时,结构将更容易发生大变形、滑移失稳和倾覆失稳等破坏。
[1] 徐继祖,李维杨,汪克让.海洋工程结构动力分析[M].天津:天津大学出版社,1992.
[2] 何晓宇,李宏男.地震与波浪联合作用下海洋平台动力特性分析[J].海洋工程,2007,25(3):18-25.
[3] 赵晶瑞.自升式平台风暴自存状态桩腿动静强度分析[D].大连:大连理工大学,2002.
[4] 中国船级社.海上平台状态方法指南[M].北京:人民交通出版社,2005.
[5] 聂武,刘玉秋.海洋工程结构动力分析[M].哈尔滨:哈尔滨工程大学出版社,2002.
[6] 柳春光,齐念.考虑流固耦合作用的深水桥墩地震响应分析[J].防灾减灾工程学报,2009,29(4):433-436.
[7] 何晓宇.环境激励下海洋平台多维地震反应分析及控制[D].大连:大连理工大学,2009.
[8] 柳春光,金书成.损伤和缺陷对海洋平台抗冰抗震性能的影响[J].世界地震工程,2009,25(4):70-74.
