基于岩石切削理论的超大型绞吸挖泥船绞刀动载荷分析
2011-03-12姚建伟杨启
姚建伟,杨启
(上海交通大学船舶海洋与建筑工程学院,海洋工程国家重点实验室,上海 200240)
0 引言
随着港口吞吐量的迅猛增加和船舶吃水量的增大,我国的港口建设从原有的以港内扩建为主转变为在无遮掩的外海地区建设新港口、开辟新港区。由于很多港口都拟建在珊瑚礁和岩层海岸带上,而珊瑚礁和海底硬质岩石属于一种特殊的疏浚物质,因此岩石疏浚的问题也就变得越来越突出。传统的水下岩石爆破技术不但生产成本高,生产效率低,而且对海底环境污染极大。而基于疏浚泥土理论所设计的挖泥船并不适用于疏浚强度很大的岩石。国内外绞吸挖泥船在疏浚岩石时,施工装备磨损和振动疲劳破坏的现象时有发生[1-2]。国内外对疏浚岩石理论和实践方面的研究极少,目前仅有的几家能够研发疏浚岩石关键设备的单位都没有公布其研究成果。这种形势下,迫切需要研究绞吸挖泥船岩石切削理论,并以此为基础研发新的岩石疏浚装备。进行疏浚岩石关键设备的自主创新和国产化,具有重要的工程实用价值。
1 绞刀载荷模型建立
1.1 绞刀运动学模型建立
绞刀头总体运动可以近似分解为平动和转动,平动主要是沿绞刀头行进方向随时间变化的运动,实际上在绞刀头行进方向上的运动为绞刀头绕定位桩的旋转运动,因为绞刀头直径相比于绞刀头绕定位桩旋转的直径而言相对较小,所以近似可以看为是平动;转动即在挖岩过程中绕绞刀轴的转动。设平动方向为z轴,转动轴为y轴,vs为绞刀头横移速度。如图1所示。
绞刀头总体运动由平动和转动组成,为了能用同一矩阵表示平动和转动,有必要引入齐次变化矩阵。在三维直角坐标系中,可以用向量 [xit,yit,zit]T表示i号绞刀齿在t时刻的坐标,则 [xit,yit,zit,1]T表示 [xit,yit,zit]T的齐次坐标。平移的齐次坐标矩阵为:

图1 绞刀运动图

假设绞刀头以转速n绕y轴逆时针旋转,经过时间t所转过的角度为2πnt,则其转动的齐次坐标矩阵为:

平移加旋转的齐次变换矩阵:

通过上面的分析,得出了绞刀头旋转加平移运动的齐次变换矩阵,实际上也是刀齿的齐次变换矩阵,因为绞刀齿是固定在绞刀头上随着绞刀头运动而运动。确定好刀齿初始时刻的空间位置坐标后,再用组合的齐次变换矩阵左乘绞刀齿初始时刻的位置坐标矩阵就可以得到任意时刻刀齿的空间坐标。
下面来对刀齿初始时刻空间坐标进行分析,以 [xi0,yi0,zi0,1]T表示第一个刀臂i号刀齿的起始齐次坐标,在初始时刻,第一个绞刀外刀臂轮廓线上的绞刀齿三维坐标为[3]:

式中:N为绞刀切削介质的标准贯入击数;参数D为绞刀外径;k为刀臂轮廓线的外展系数;Ω1为刀臂外轮廓线包角;α为同一绞刀臂上相邻齿角度;d1为轮毂外径。式(4)中反映了刀齿在绞刀头上的位置,疏浚不同土质的绞刀,其绞刀大小是不一样的,刀齿的相对位置也会改变。
根据绞刀臂的对称性,其余绞刀臂的刀齿可以通过把第一条绞刀臂上的绞刀齿绕着y轴旋转一定角度得到(β为相邻两刀臂的旋转角度):

根据以上原理,运用matlab6.5绘制了绞刀三维图形,如图2所示。

图2 绞刀三维外轮廓侧向数值仿真视图
由上面公式已计算出所有刀齿在初始时刻所组成的齐次坐标矩阵G0,以Gt表示刀齿任意时刻t的齐次坐标矩阵,则Gt可表示为:

1.2 绞刀动力学模型建立
绞刀刀齿在破碎岩石的过程中,在时刻t刀齿i同时受到切向力Fτit,法向力Fnit和轴向力Fait的作用。借鉴已经成熟的螺旋破碎岩石的研究成果,并根据实际情况作出一定的修改,计算公式可表示如下[4-6]:

式中:A为岩石截割阻抗;σy为岩石单轴饱和抗压强度;b为刀齿截刃宽度,依刀齿实际尺寸而定;B为岩石的脆性程度指数;hit为t时刻截齿切割岩石厚度;l0为平均截线距;k为与截割工况有关的系数;f为截割阻力系数;β为截齿相对截割机构牵引方向的安装角度;kn为平均接触应力对单向抗压强度的比值;Kn为锋利截齿牵引力对截割力的比值;sd为截齿磨损面积;c,d,e均为经验系数。对绞刀结构参数和刀齿结构参数的选取是依据成熟的绞刀和刀齿模型,岩石的性能指数依据绞吸挖泥船疏浚岩石的地质特性选取,这里主要对延展性比较好的岩石进行研究。
在这里对轴向力的求法进行改进,因为上述理论是建立在圆柱切削的基础上,而绞刀切削岩石为球锥形切削,轴向力的产生机制不一样,所以调整为根据绞刀法向力求出轴向力[7](k为齿形弧度角,如图3所示)。

图3 圆锥形绞刀齿位弧度角

上面所建立的绞刀齿力学模型,绞刀齿力的方向分别为切向、法向和轴向,为了求解绞刀所受的力,必须将每个绞刀齿切向力、法向力和轴向力都分解到由图1所表示的x,y和z轴方向上。通过分析可知,轴向力与y轴是平行的,而切向力、法向力分布在xoz平面内。因此,只需要将切向力和法向力分解到x和z轴方向上,就可以将每个绞刀齿切向力、轴向力和侧向力分解到x,y和z轴方向上,变换公式为(θ为任意时刻刀齿转动角度):

绞刀所受的力主要是刀齿的合力,计算公式如下(m为绞刀齿的总数目):

这里称x轴方向的合力为竖直合力,y轴方向的合力为轴向合力,z轴方向的合力为水平合力。
1.3 绞刀切削岩石的关键点分析
1.3.1 切削层厚度
切削层厚度hi是当前刀齿的切削路径和上一刀齿切削路径之间的范围,hi的大小是随刀片运动而变化的。薄片的厚度hi如图4所示,假设刀臂相对圆心O已转过角度θ,过刀臂端点做一条切削层的水平截线,图4中线段L即为所求的切削薄层的厚度。设切削横移速度为vs,一般情况下绞刀横移速度远小于刀臂端点A点的旋转线速度,所以A,B,C所围成的三角形可近似看作直角三角形,于是表达式为:

上面所假设的为圆柱型切削的状态,实际绞刀为圆锥状绞刀,如图3所示得到的切削厚度还需要乘以齿形弧度角k:
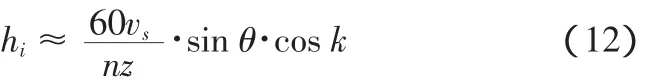

图4 圆柱形绞刀切削厚度
1.3.2 绞刀齿是否处于切削状态的判定条件
某工况下挖岩绞刀深度角Ω如图5所示,则绞刀齿处于切削状态的判定条件为:sin θi≥0,cosθi≥cosΩ(θi为第i个绞刀齿t时间内转动的角度,逆时针为正)。

图5 绞刀切削岩石深度角
2 数值仿真系统简介
2.1 绞刀切削岩石数值仿真功能模块
如图6所示,通过仿真程序功能模块的划分,可以依据功能模块来编制函数,通过不同函数来实现不同模块的功能。写函数的思路是:先写最底层功能模块的函数,调试通过后,依次往上写更大的功能模块;依据该思路分别写完绞刀运动学仿真模块和绞刀力学仿真模块后,再将该两大模块进行连接和调试,最终实现绞刀头切削过程的仿真。

图6 绞刀切削岩石仿真功能模块示意图
2.2 绞刀切削岩石过程仿真程序的图形用户界面
为了使绞刀头切削过程仿真程序更方便操作和直观,本文利用ActiveX技术进行Matlab/VB混合编程[8],从而将Matlab强大的数学计算功能与VB在图形化用户界面开发方面的优势有效地结合起来,采用Matlab6.5进行绞刀载荷波动性核心程序编制和绘图工作[9]。利用VB6.0在编制用户界面方面的优势,编制了绞刀仿真载荷用户界面,如图7所示。

图7 绞刀切削岩石过程仿真系统
3 实船应用以及计算结果分析处理
以上海交通大学船舶与海洋工程研究所设计的绞刀功率为4 200 kW超大型自航绞吸挖泥船切削岩石绞刀为模型,依据上述理论,进行了绞刀受力以及载荷波动性的分析研究。
所取绞刀基本参数如下:
绞刀头:VOSTA tube/2 530×830/6
大圈内直径:2 530 mm
大圈外直径:3 000mm
大圈到轮毂底:830mm
刀臂数量:6
绞刀额定输出功率:4 200 kW
所用齿:T6.02
绞刀横移速度:0.048m/s
刀臂包角:75°
绞刀额定转速为:32 r/min
所疏浚岩石的特性:
岩石的惯性击入系数:40
岩石抗压强度:40MPa
3.1 计算结果可靠性验证
取额定载荷工况即绞刀转速为32 r/min,绞刀横向移动速度为0.048m/s,绞刀切削深度角为165°,得到此时绞刀消耗的平均功率为4 304 kW(如图7所示),而所取的验证船在最大载荷工况下的绞刀额定消耗功率为4 200 kW。考虑到实际情况与数值模拟的差异性,此数值模拟结果可以接受,这验证了上述理论研究的正确性。
同理,对绞刀功率为2 000 kW的绞吸挖泥船进行验证。此船额定工况下转速为30 r/min,绞刀移动速度为0.065m/s,绞刀切削深度角为90°,所能挖掘岩石的抗压强度为30MPa。由于挖岩绞刀的通用性,对2 000 kW绞吸挖泥船绞刀采用与4 200 kW绞吸挖泥船相同的绞刀。此时得到2 000 kW绞吸挖泥船绞刀所消耗平均功率为2 105 kW,而本船在额定工况下的绞刀消耗功率为2 000 kW,考虑到实际情况与数值模拟的差异性,此数值模拟结果可以接受,这验证了上述理论可适用于不同功率绞吸挖泥船。
3.2 绞刀所受载荷波动性分析
这里取额定工况,即绞刀转速为32 r/min,绞刀横向移动速度为0.048m/s,绞刀切削深度角为165°来进行绞刀所受载荷以及功率波动分析,载荷波动分析详细图如图8。
从图8中可以看出,绞刀由于对称性在每相隔一定转角范围内出现载荷波动重复。图8(a)中功率最大值为4 439 kW;图8(b)中绞刀水平合力最大值为1 369 kN;图8(c)中绞刀竖直合力最大值为905 kN。图8(d)在轴向最大值为775 kN。通过对图8绞刀切削功率为4 200 kW绞刀切削岩石所产生的载荷时域信号预处理,去除直流分量和趋势项,再作FFT的分析[11]。得到4 200 kW绞刀切削岩石的频域信号,如图9所示。

图8 在最大工况下的载荷波动图

图9 最大工况下的频谱图
由图9可得出,在最大工况条件下4 200 kW绞刀主激振频率为3.2Hz。上述主激振频率只是在一种工况下取得,通过数值仿真系统对4 200 kW绞刀在不同工况下,也就是在不同切削齿数下模拟得出:绞刀高阶频率会随着绞刀每次切削深度和实际切削岩石齿数的不同而变化,但绞刀低阶主频率在额定转速下都基本不变,而且此激振频率下振幅都比较大。进一步分析得出此激振频率主要与绞刀转速和绞刀刀臂数有关。考虑绞刀一般都是6个刀臂,切削岩石一般都在额定转速下工作,同时由于桥架低频下阻尼很小,动力放大系数会很大,如果产生共振其危害性会很大[12];而高频振动随切削工况不同变化较大,且其振幅相对偏小,如果某一工况下高阶激振频率对桥架振动影响比较大,可以通过变化切削状态的方式来避开。综合以上因素,可把低阶主频率3.2 Hz定位为4 200 kW绞刀在额定转速下切削岩石所产生的主激振频率。
同理,可分析出其它切削岩石的绞刀所产生主激振频率。通过对不同绞刀进行分析,得出绞刀挖掘岩石主激振频率可按照下列公式计算。

式中:f为绞刀激振频率,Hz;z为绞刀刀臂数;n为绞刀转速,r/min。
4 结语
通过建立绞刀切削岩石载荷模型,利用Matlab/VB混合编程技术编制了相关仿真系统,对绞刀切削岩石情况进行了平均载荷分析以及载荷波动性的分析,从定量的角度分析出了绞刀切削岩石所受的载荷大小以及载荷情况变化。通过对两艘不同绞刀切削功率的绞吸挖泥船进行分析,得出本文所提出的理论具有很好的适用性,并通过时域和频域分析对疏浚岩石绞刀的载荷波动性和主激振频率进行了研究。为以后进行绞刀架以及整个挖泥船船体强度和动力性能分析提供了参考依据,为研发能够疏浚岩石的国产优质超大型绞吸挖泥船奠定了基础,所编载荷仿真软件可在以后经过实验对所取参数不断完善后,用于实船中对载荷受力进行实时监控,优化切削岩石产量,实现最大经济效益。同时论文研究结果可为深海采矿提供一定参考。
[1] 高伟.绞吸船挖岩工艺研究[D].天津:天津大学,2006.
[2] Verhoef PNW.Wear of Rock Cutting Tools[M].Taylor&Francis Ltd,1997:1-2.
[3] 朱文亮.疏浚实验平台开发一绞刀三维造型及土壤切削实验监控系统[D].南京:河海大学,2007.
[4] 别隆A H.卡赞斯基AC.煤炭切削原理[M].工兴柞译.北京:中国工业出版社,1965.
[5] 苑忠国.采掘机械[M].北京:冶金工业出版社,2009.
[6] 刘勇.深海钻结壳螺旋滚筒切削采集法的理论及实验研究[D].长沙:中南大学,2002.
[7] Vlasblom W J.Lecture WB3413/OE4626 Dredging Processes[M].Netherlands:Delft University of Technology.2007:44-45.
[8] 胡智文,陈连运.利用ActiveX技术的VB与Matlab间的无缝集成[J].计算机工程,2004,30(7):64-65.
[9] 苏金明,阮沈勇.MATLAB实用教程[M].北京:电子工业出版,2005.
[10] Jaap L van Overhagen,Marcel Boor,Andre Kik,et al.On the Conceptual Design of Large Cutter Suction Dredgers;Considerations for Making Choices[C]//Proceeding of CEDA Dredging.JAN,2005
[11] 万永革.数字信号处理的MATLAB实现[M].北京:科学出版社,2007:73-85.
[12] 金咸定,张保玉.船体振动学[M].上海:上海交通大学出版社,2000:110-111.
