一种基于改进的SOFM神经网络的图像无损压缩方法*

陈善学 ，王佳果 ，彭 娟 ，张本强

（1.重庆邮电大学移动通信安全技术实验室 重庆 400065；2.中兴通讯股份有限公司 深圳 518057）

1 引言

香农的信息论图像的压缩方法可以分为无损压缩和有损压缩。无损压缩的特点是失真度很低但压缩比较小；而有损压缩虽然有较高的失真率但可以获得大压缩比。由于在军事、公安、遥感图像等方面对图像失真度要求低，使得无损压缩成为图像处理的一个重要研究方向。

矢量量化[1,2](vector quantization，VQ)是一种高效的有损数据压缩技术，因其具有压缩比高、编解码速度快的特点，被广泛地应用于语音编码和图像的压缩系统。其基本思想是：把图像看成是一串数据，设这一串数据大小为m，把它截 M段(一般每段相等，如为 k)，即把 m个数据变成了M个矢量，再把这M个矢量分成N组，为每个组挑选一个数据矢量作为这个组的代表，如第j个组的代表为yj，j=0,1,…,N-1。而压缩就是图像中的数据矢量，如果属于第j个组，则这个数据矢量就用这个组的代表矢量代替，这时的编码就是在相应的位置上记下编号j，而不必记下矢量本身。集合{yj,j＝0,1,…,N-1}称为码书，N为码书长度或码书大小。

本文采用基于SOFM[3](self-organizing feature maps，自组织特征映射神经网络)矢量量化的图像无损压缩方法，该方法首先用SOFM神经网络对图像进行矢量量化，然后将原图像与经矢量量化后恢复的图像作差值，将矢量量化后的数据作自适应算术编码，而差值图像作变长编码。在接收方将矢量量化后恢复的图像和差值图像相加，即可得到解压后的图像。实验结果表明了该算法的压缩比比传统的DPCM无损压缩最高可提升40%,证明了其有效性。

2 基本SOFM算法

芬兰学者Kohonen提出的SOFM算法是一种基于自组织特征神经网络无监督学习的聚类过程[4,5]。自组织特征神经网络是一种具有侧向联想能力的双层结构网络，一般由输入层和输出层构成，输出节点呈二维阵列分布，如图1所示，每个输入节点与输出节点之间用可变权值连接，每个输出节点都有一个拓扑邻域，邻域随时间而变化。竞争层由N个神经元组成，输入层由M个神经元组成，输入层各神经元与竞争层各神经元之间实现全互连接。有时竞争层各神经元之间也实现相邻神经元侧抑制连接[6]。

SOFM网络的竞争层神经元个数等于码书的尺寸Q，输入层神经元通过可变的权值与竞争层神经元相连，竞争层所有神经元通过相互竞争和自适应学习算法调整连接权值，训练结束后竞争层所有神经元的权值就构成了码书。

设训练矢量数为N，训练矢量集表示为X=(X1,X2,…,XN)，网络有N个输入节点，竞争层有Q个神经元（等于码书大小），由输入层到竞争层的连接权值为Wij，i=[1,…,Q]，j=[1,…,N]，其算法如下。

（1）将初始化连接权值 Wij赋予随机值。

（2）从训练集合中选择训练矢量 Xk，k∈[1，N]，用并行方式输入到竞争层的每一个神经元。

（3）计算Xk与各神经元(即Wij)间的失真，选择具有最小失真的神经元g为获胜神经元，按式（2）调整神经元g及g的拓扑领域内各码字的权值，其他权值保持不变，即：

其中，i∈NEj(t)，NEj(t)为码字 g 的拓扑领域，t为迭代次数。α(t)为学习速率因子，一般选为：

其中，tmax为总的迭代次数，t为当前迭代次数，α0取[0,1]。

（4）对所有训练输入模式，重复步骤（2）、（3），直到算法收敛或达到初始设定的最大迭代次数。

3 改进的SOFM算法

通过上面的描述，发现基本SOFM算法在某些环节上还是存在缺陷的[7]，如其获得获胜神经的环节存在失真计算量太大的问题，而另一方面，由于训练数据统计特性的影响，在竞争层有些神经元获胜的概率大且权值经常调整，而有些神经元的权值很少调整，影响了算法的收敛。针对以上几点，本文对基本SOFM算法进行改进，提高了SOFM网络的性能。

3.1 搜索获胜神经元

在上述基本SOFM算法中，每选择一次获胜神经元都需对输入矢量与每个码字进行失真计算，也就是对所有神经元进行穷尽搜索，这样需要Q次失真计算，N个训练矢量就需要MQ次失真计算；如果平均迭代次数为R，则共需要MNR次失真计算，这样的计算量是非常大的。基于此，在选择获胜神经元时，有必要采取一定的措施减少大量的失真计算。陆哲明等根据距离不等式判决提出一种改进的SOFM算法可以加快学习的速度，其详细的改进方法参见参考文献[8]。

3.2 引入频率敏感因子[9]

由于训练数据统计特性的影响，在竞争层有些神经元获胜的概率大，其权值经常调整，而有些神经元的权值很少调整。为了使每个神经元都能够被充分利用，引入了敏感因子βi[10]，其初始值为1，每当竞争层神经元g在竞争层过程中获胜1次，βi加1，即敏感因子为获胜神经元获胜次数，将失真误差修正为 di=βi×di。因此，随着 βi的增加，竞争层神经元g再次成为获胜神经元的机会减小，增大了其他神经元的获胜机会，从而提高了算法的收敛速度。

3.3 改进的SOFM算法

改进的SOFM算法如下。

（1）初始化权值 Wij，i=[1,…,Q],j=[1,…,N]，可从训练序列中随机选取。

（2）从训练集合中选择训练矢量 Xk，k∈[1，N]，用并行方式输入到竞争层的每一个神经元。

（3）将一个矢量各分量的和定义为 SXk，k∈[1，N],码字和值定义为SWi，可以证明：

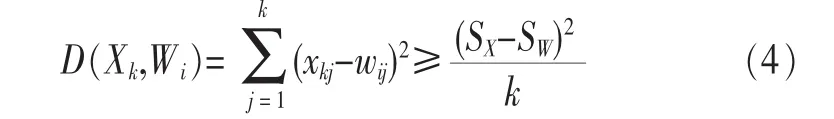
设当前的最小失真为dmin，并令MD=Kdmin，若有：

则根据式（4）有：

因此，可以在每次搜索获胜神经元前，预先计算Q个码字的和值SWi，并保存在码书中，同时在搜索获胜神经元过程中预先计算MD，然后判断码字Wi的和值 SWi是否满足式（5），若满足，则码字Wi可以排除，而免去计算失真误差。

（4）设通过步骤（3）找到的获胜神经元为 g，则按照下面的方法调整神经元g及g的拓扑领域内各码字的权值，其他权值保持不变，即：

（5）对所有训练输入模式，重复步骤（2）～（4），直到算法收敛或达到初始设定的最大迭代次数。

4 实验仿真结果

本文所采用压缩算法如图2所示，该算法首先采用改进的SOFM算法进行矢量量化，然后将原图像与矢量量化后恢复的图像作差值，将量化后的数据作自适应算术编码，而对于差值图像，虽然其像素范围为-255～255，看起来比原始图像的像素值增加了一倍，但实际上，数据大多为0值或在0值周围徘徊，如采用码书尺寸为2048时，差值图像的0值数约占总像素的近42%。对出现概率高和出现概率低的值分别赋予较短和较长的码字，就能够减少整体数据量。这种根据数据的值改变码字长度的方法称为变长编码(variable-length coding),其中霍夫曼编码是代表性的变长编码之一。而在接收方将量化后恢复的图像和差值图像相加，即可得到解压后的图像。

本算法选用256×256×8 bit的灰度图像 Lena作为测试对象，同时将图像分为4×4子块，将每一块16个像素灰度值作为一个训练矢量。首先比较基本的SOFM算法和改进的SOFM的算法的码书设计时间和峰值信噪比(PSNR)，不同条件下基于SOFM算法矢量量化的比较见表1；其次将本算法和传统的DPCM无损压缩算法相比较，JPEG的无损压缩采用基于DPCM (differential pulse code modulation)的方式进行压缩，该方法的压缩比平均可达1.54[9]，不同码书大小下算法压缩比见表2。

表1 不同条件下基于SOFM算法矢量量化的比较

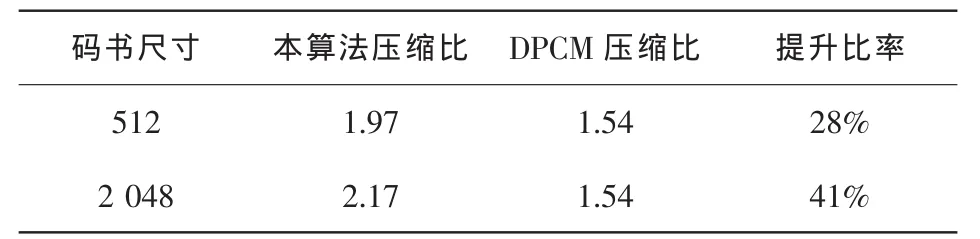
表2 不同码书大小下算法压缩比

5 结束语

通过上述实验，得到如下结论。

·通过实验数据(见表1)发现，采用改进后的 SOFM设计码书，可以有效地减小码书设计时间，提高码书性能，相对于基本算法，码书设计时间减少了约70%，图像效果、编码质量均提高0.4～0.9 dB。而采用改进的SOFM图像无损压缩算法，相比传统的DPCM无损压缩算法的压缩比最高可提高40%，证明了算法的有效性。

图2 基于SOFM的无损压缩算法

·码书大小对本算法最后的压缩比有着重要的影响，从表2中可以很明显地看出，Q=512与Q=2048之间有着差别，码书尺寸较小时矢量量化后数据编码数据量也较小，但差值图像的编码数据量较大；码书尺寸较大时，差值图像编码数据量较小，但矢量量化后数据编码数据量较大。所以如何选择这两者之间的最佳点，还需要作进一步的研究。

1 Linde Y,Buzo A,Gray R M.An algorithm for vector quantizer design.IEEE Transactionson Commemoration(S0090-6778),1980,28(1):84～95

2 Geraho A,Gray R M.Vector quantization and signal compression.Boston,MA Kluwer,1992

3 Nassrabadi N M,Feng Y.Vector quantization of image based upon the Kohonen self-organizing feature maps.In:Proc IEEE int Conf Neural Networks,San Digeo,CA,1988

4 (美)Martin T,Hagan Howard B,Demuth著.戴葵等译.神经网络设计.北京：机械工业出版社，2002

5 Amerijckx C,Legaty J D,Verle-Ysen M.Image compression using self-organizing maps.System Analysis Modeling Simulation,2003,43(11):1529～1543

6 Sambu Seo,Klaus Obermayer.Self-organizing maps and clustering methods for matrix data.Neurocomputing,2006(69):2033～2040

7 孙圣,陆哲明.矢量量化技术及应用.北京：科学出版社，2002

8 段勇.改进的SOFM及其在矢量量化中的应用.系统仿真学报,2006,18(3):718～721

9 王黎明，赵英亮，韩众程，耀瑜.基于JPEG-Ls框架的无损压缩技术研究.电脑开发与应用，2002

10 Bei C D,Gray R M.An improvement of the minimum distortion encoding algorithm for vector quantization.IEEE Transactions on Communications,1985,33(10):1132～1133