中小口径次镜支撑结构的动力学性能分析

贾庆莲，邓文渊

（中国科学院 长春光学精密机械与物理研究所，长春 130033）

在现代望远镜系统中，卡塞格林系统由于在主镜和次镜之间没有中间像，具有结构紧凑、尺寸小、筒长短以及轴上分辨率高等特点得到广泛的应用［1，2］。对次镜支撑结构而言，一般要求结构简单、易于装配、有良好的刚性及稳定性，而且要求遮拦比小。在实际使用过程中，既有口径在几百毫米的小口径系统，也有口径多达几米的大型望远镜系统［3］，这就对次镜的支撑结构提出了很多要求，选择合适的支撑结构成为影响望远系统性能的一个关键因素。

在常用的次镜支撑结构中，典型的有三翼对称结构、三翼偏置结构、四翼十字型对称结构以及四翼十字型偏置结构等［4-7］。这些结构的共同点是在次镜与次镜支架之间采用薄片梁连接，这种筋板式的薄片梁如果设计合理即可以保证整体结构的稳定性，又可以尽量减小遮拦比。

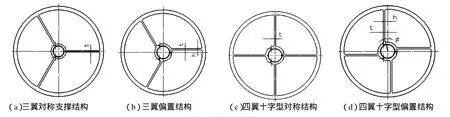
图1 次镜支撑结构Fig.1 Supporting structure of second mirror

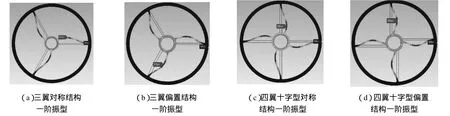
图2 次镜支撑结构的一阶振型Fig.2 First order resonant model for the structure of second mirror

在影响结构稳定性的因素中，梁片的厚度和宽度越大，则稳定性越好，主、次镜的口径差越大，遮拦比越小，有利于光学系统优质成像，但也同时加长了梁片长度，降低了支撑结构的刚度及谐振频率。

因此分析梁片的厚度变化及系统的口径变化对支撑结构的谐振频率及轴向变形的影响，并由此针对一定的口径选取合适的梁片及结构是望远镜优化设计的前提，也正是本文的研究重点。

1 次镜支撑结构的动力学模型

目前典型的光机结构中，次镜支撑结构如图1所示。为了使问题简化，假定次镜组件的质量沿圆周方向和光轴方向均匀分布，那么连接次镜支撑座与次镜之间的薄片梁在支撑端就会受到均匀载荷的作用而产生振动，假定次镜支撑端固定，而薄片梁与次镜连接处为固定约束，在由于薄片梁的抗弯曲能力较差，由此造成次镜支撑结构的一阶振型主要是薄片梁的弯曲振动，如图2所示。

在对称结构中取任意一条薄片梁，基于弹性力学理论［8］，建立其动力学分析模型，如图3所示。梁片在x、y方向的变形分别为x、y，对应的变形角为 。

图3 薄片梁的动力学分析模型Fig.3 Dynamic analysis model for the plate

其谐振频率为［5］：

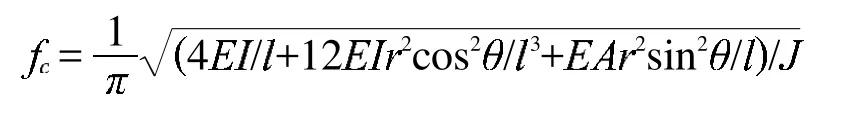
式中，r为次镜的关径，E为梁片材料的弹性模量，I为梁片的惯性矩，A为梁片面积，l为梁片的长度（l=D/2 ），J为次镜及其组件的转动惯量。

2 次镜支撑结构的有限元分析及一阶谐振频率的计算结果

针对小口径中波红外测量系统，其D=220mm，d=40mm，t=3mm，取其偏置 h=6mm，材料为铸铝，针对上述四种结构，其一阶谐振频率为三翼对称结构为1139Hz，三翼偏置结构为1601Hz，四翼十字型对称结构 1129Hz，四翼十字型偏置结构为1805Hz。从结果可以看出，这种小口径的光学系统，一阶谐振频率最高的结构为四翼偏置结构，其次为三翼偏置结构，最小的为四翼十字型对称结构。无论哪种次镜支撑结构其一阶谐振频率都很高，因此综合加工工艺及制造成本等多方面因素，选取结构最简单的三翼对称结构就能良好的满足要求。

当系统口径增加到为650mm时，其一阶谐振频率为三翼对称结构为 197Hz，三翼偏置结构为277Hz，四翼十字型对称结构170Hz，四翼十字型偏置结构为297Hz。结果可以看出，一阶谐振频率最高的结构为四翼偏置结构，其次为三翼偏置结构，最小的为四翼十字型对称结构，其规律与口径为220mm时完全一致。

如果保证遮拦比一致，材料选为 A3钢，针对三翼对称结构，通光口径从220mm到800mm，其一阶谐振频率变化曲线如图4所示。

从图4中可以看出，随着通光口径的增加，次镜组件的一阶谐振频率下降很快，当系统口径达到800mm时，一阶谐振频率已经降到129Hz，如果再增加系统口径，这种三翼对称支撑结构就不能满足系统高稳定性的要求了。

针对系统口径为800mm的四翼偏置支撑结构，改变梁片的厚度，其一阶谐振频率的变化曲线如图5所示，其沿轴向的变形量如图6所示。

从图5可以看出随着梁片厚度的增加，次镜支撑组件的一阶谐振频率也在增加，对四翼偏置结构当梁片厚度为 4mm时，其谐振频率已经达到208Hz。而对三翼对称结构当梁片厚度为4mm时，其谐振频率为96Hz，当梁片厚度增加到9mm时，其谐振频率才为198Hz，比四翼偏置结构的小很多。

从图6可以看出，随着梁片厚度的增加，次镜组件沿光轴方向的变形量在减小，当梁自厚度为3mm时，轴向变形达到0.077mm，而当梁片厚度增加到9mm时，轴向变形量已经减小到0.037mm。

从图5和图6结果可以看出，随着梁片厚度的增加，次镜支撑结构的刚度增加，结构稳定性加强，由此造成了一阶谐振频率的提高和轴向变形量的减小。

3 结论

本文针对口径在800mm以内的中小口径卡塞格林系统的次镜支撑结构进行了动力学分析，分析了次镜支撑结构中薄片梁的刚度及其变形。经过有限元分析，利用Ansys软件分析了几种常用结构的一阶振型。

有限元仿真结果表明当系统通光口径为220mm时，几种结构的一阶谐振频率都达到一千Hz以上，因此选用加工工艺简单、成本较低的三翼对称支撑结构就能很好的满足要求。但当系统口径达到650mm时，几种不同结构的一阶谐振频率都已经下降到300Hz以下，其中四翼对称结构只有170Hz。

当保证系统遮拦比一致时，针对三翼对称支撑结构，当通光口径达到800mm时，其一阶谐振频率已经下降到129Hz。

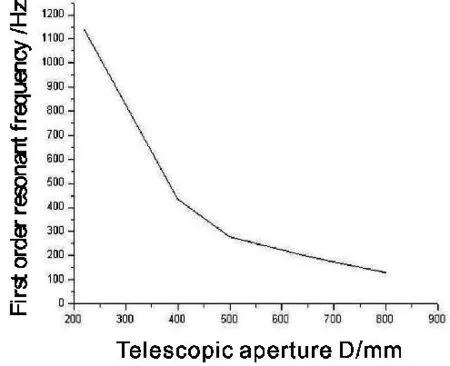
图4 通光口径对一阶谐振频率的影响Fig.4 Influence of telescopic aperture on first order resonant frequency

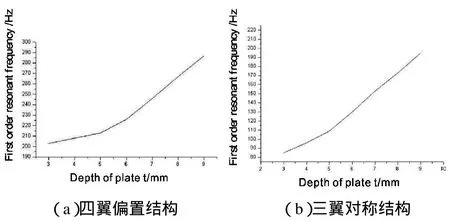
图5 梁片厚度对一阶谐振频率的影响Fig.5 Influence of width of plate on first order resonant frequency

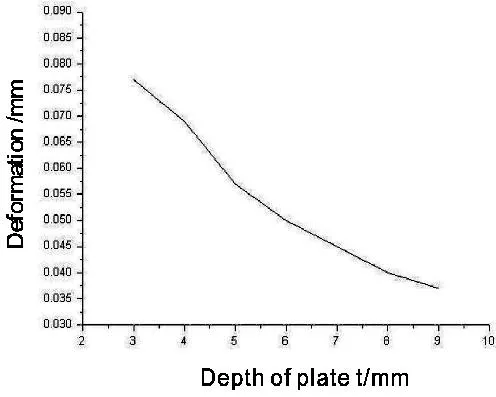
图6 梁片厚度对次镜轴向变形的影响Fig.6 Influence of width of plate on the optical-axis deformation of second mirror

当增加梁片厚度时，一阶谐振频率都会提高，但相比较而言，三翼对称结构的频率增加速率较大，而四翼偏置结构的增加速度率较小。同样当梁片厚度从3mm增加到9mm时，次镜组件的轴向变形减小了两倍。

［1］胡家升.光学工程导论［M］.大连：大连理工大学出版社，2002.

［2］程景全.天文望远镜原理和设计［M］.北京：科学技术出版社，2003.

［3］惠彬，李景镇，裴云天，等.大口径折反射式光学系统的光机结构分析［J］.光子学报，2006，35（7）：1117-1120.

［4］张林波，任戈，陈洪斌.四翼十字形中心支撑结构的动力学分析［J］.光学精密工程，2003，11（5）：472-475.

［5］梁文科，刘顺发.次镜支撑结构的力学性能分析［J］.仪器仪表学报，2007，28（5）：859-863.

［6］陈景全，李国平.四翼梁式十字形中心支撑的力学特性［J］.天文仪器与技术，1988，1：5-10.

［7］王富国，张景旭，杨飞，等.四翼梁式次镜支撑结构的研究［J］.光子学报，2009，38（3）：674-676.

［8］曲庆璋，章权，季求知，等.弹性板理论［M］.北京：人民交通出版社，2000.

［9］杨利伟，李志荣.一种基于有限元分析的柔性支撑结构设计［J］.长春理工大学学报，2008，31（1）：49-52.