我国科技人才对经济增长贡献率的实证研究
2011-03-09蒋正明张书凤李国昊田红云
蒋正明,张书凤,李国昊,田红云
(1.南京航空航天大学 经管学院,南京 210016;2.江苏大学 工商管理学院,江苏 镇江 212013)
1 研究预设
预设1:对研究时限的选择,考虑到数据的可获得性以及研究的现实意义,本文选择1988~2008年共跨越20年的时间。
预设2:假设经济增长要素中仅存在物质资本、一般劳动和科技人才三个基本要素。
预设3:假设生产函数满足类似柯布-道格拉斯生产函数的形式。
预设4:假设生产函数满足希克斯中性技术进步,且科技进步速度不变。
2 变量及基础数据
2.1 经济总量
目前学者对经济总量的变量选择,一般采取的是国内生产总值(GDP)。主要有名义GDP和实际GDP两种选择方法。考虑到通货膨胀对国内生产总值的影响,本文认为实际GDP可以较好的反映一国或地区经济实际总量,因此选择实际GDP。由于现有国内统计年鉴中直接可以获得的数据是名义GDP(即以当年价格反映的国内生产总值)以及GDP指数,本文根据这两个指标,采用计算的方法,获得我国实际GDP的数据(以1952年为基年)。
2.2 物质资本
对于物质资本的变量选择,目前学者主要采用了固定资产投资额、固定资本形成额、资本形成额、固定资本存量、资本存量等5个变量。而大多数学者越来越倾向于采用固定资本存量或资本存量,事实上在生产函数中物质资本作为一种投入要素,是实际投入到生产过程中的资本,而固定资产投资额、固定资本形成额、资本形成额只能代表当年固定资本或资本的增加额,不能表示当年所有投入到生产过程中的资本要素。鉴于此,本文采用资本存量作为物质资本。物质资本包括固定资本和流动资本。
对于固定资本存量的测算,目前大多数研究人员采用的是由Goldsmith于1951年开创的永续盘存法。其基本公式如下:

其中:Kt表示第t年的固定资本存量,Kt-1表示第t-1年的固定资本存量,It表示第t年的固定资本投资,ρt表示第t年的折旧率。
现有研究基本上都以永续盘存法为基础进行的,但是在细节处理上却有很大差异。比较有代表性的测算公式如下:
邹至庄(Chow,1993)采用的计算公式为:

其中,NIt表示第t年的实际净投资。
贺菊煌(1992)采用的计算公式为:

其中,At表示第t年的积累。
王小鲁和樊纲(2000)采用的计算公式为:

其中,Kt表示以1952年不变价的第t年的固定资存量,Kt-1表示以1952年不变价的第t-1年的固定资本存量,FFKt表示第t年的固定资产形成额,Dt表示第t年的折旧,表示第t年的固定资产投资价格指数。
对资本存量测算本文从以下四个方面考虑:
第一,基期固定资本存量的确定。由于现有统计年鉴对固定资本存量的数据没有公布,对基期固定资本存量的确定只能采用估算法。固定资本存量本文在张军(2003)的基础上,加上土地资本的价值,土地资本的价值本文采用邹至庄的观点,将1952年土地资本的价值设定为720亿元,因此本文认为1952年我国固定资本存量的价值为1520亿元,由此推算1952年我国流动资本(主要是存货)的价值为480亿元。
第二,资本增量的确定。主要有两种选择,一是全社会固定资产投资额,二是固定资本形成额,三是资本形成额。从实际物质资本增加来看,全社会固定资产投资往往存在浪费,与实际固定资本形成额存在差异,本文认为采用资本形成额更加合理,因此本文采取资本形成额作为资本增量。
第三,实际固定资本投资的确定。由于当年固定资本形成额没有考虑通货膨胀的影响,因此需要采用固定资本形成指数进行换算。2004年以前的资本形成指数在《中国国内生产总值核算历史资料:1952~1995》以及《中国国内生产总值核算-历史资料 1952~2004》中公布。2005年以后的资本形成总额指数、固定资本形成总额指数以及存货增加指数是通过指数平滑法估算获得。
第四,固定资本折旧的确定。大多数学者采取的是折旧率的方法,但对折旧率的选择有所差异,本文采取10%的折旧率。
根据上述分析,本文对以1952年不变价 表示的实际资本存量以及实际固定资本存量的测算,采用如下公式:

其中,Kt表示以1952年不变价计算的第t年的资本存量,Kt-1表示以1952年不变价计算的第t-1年的资本存量,FK0表示以1952年不变价计算的第t-1年的固定资本存量,KI0表示1952年资本形成额,KIt表示以1952年=100的第t年的资本形成总额指数,ρ表示固定资本折旧率。

其中,FKt表示以1952年不变价计算的第t年的固定资本存量,FKt-1表示以1952年不变价计算的第t-1年的固定资本存量,BK0表示 1952年固定资本形成额,KIt表示以1952年=100的第t年的固定资本形成总额指数,ρ表示固定资本折旧率。
根据式(5)和式(6),计算以1952年不变价表示的1952年-2008年我国资本存量以及固定资本存量见表1。
2.3 人力资本
关于人力资本投入要素的变量选择,现有学者主要有四种方式,一是以就业人数作为人力资本投入,二是以劳动者报酬作为人力资本投入,三是以劳动者收教育年限作为人力资本投入,四是以不同类型的就业劳动者作为人力资本投入。这四种方式的主要差异在于对人力资本的衡量方法不同。本文采取第四种方式,以一般劳动者与科技人才作为衡量人力资本投入的因素。科技人才采用的是科技活动人员指标,一般劳动是用就业人数减去科技活动人员计算获得。
3 我国科技人才对经济增长贡献率的模型的构建

表1 1952~2008年我国资本存量(1952=100) 单位:亿元
C-D函数的一般形式如下:

其中:Y表示总产出或GDP,K表示物质资本,L表示劳动,A0表示技术水平。
本文引入科技人才T以及与时间相关的内含的外部技术进步速度,则式(7)变为:

式(8)两边取对数
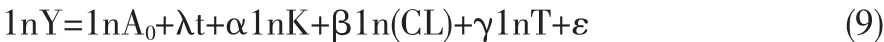
式(9)则为式(8)的线性回归方程,其中ε为随机误差项。
式(9)两边微分得:

分别用ηK、ηCL、ηT表示物质资本、一般劳动和科技人才对经济增长的贡献率,用ηA表示技术进步对经济增长的贡献率。则有:

4 模型的参数估计
根据基础数据,应用EViews 6软件进行参数估计,估计结果见表2:

表2 模型参数估计
从表 2可以看出,R-squared=0.997833,Adjusted R-squared=0.997292,模型拟合优度较好。由F=1842.109>F0.01(4,21-4-1)=4.77,显著性水平较高,F检验的相伴概率为P=0.000000<0.01,可见因变量与自变量之间线性程度较高。回归方程高度显著。
由回归系数的t值可以看出,在置信度等于0.05的条件下,C、lnK、lnCL和 lnT的回归系数的相伴概率均大于0.05,检验不能通过。
DW值等于0.574228,查n=21,k=4(不含常数项),置信度为5%的DW检验的上下界,dL=0.93,dU=1.81,可见DW<0.93,存在一阶正自相关。本文采用ARMA(p,q)(自回归移动平均)技术,通过在回归方程右边添加AR(p)或MA(q),然后检验方程的回归的DW值,经过重复试验,本文在通过添加AR(4)和AR(9),得:

应用EViews 6软件对式(12)进行参数估计
由表3可以看出,F检验,R检验均通过,且t检验中各自变量的估计参数的相伴概率均小于0.05,显著优于原模型。DW=1.865018,满足dU<DW<4-dU,不存在一阶自相关。
由于已经采用ARMA技术对原模型进行处理,因此这里不再进行多重共线性检验与异方差检验。
根据用ARMA修正的模型的参数估计,得到回归方程如下:
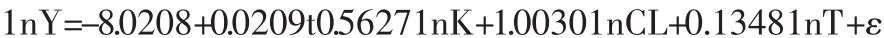


表3 用AR修正的模型的参数估计
由式(13)可以看出,物质资本的产出弹性α等于0.5627,一般劳动的产出弹性β等于1.0030,科技人才的产出弹性γ等于0.0209,科技进步速度γ等于0.0209。α+β+γ>1,存在要素规模报酬递增。
根据式(13)计算1988~2008年各要素的对经济增长的贡献率见表4。

表4 1988~2008年我国各投入要素对经济增长的贡献率 单位:%
从表4可以看出,1988~2008年我国科技人才对经济增长的平均贡献率达到0.95%左右,各年波动较大,但总体呈现上升趋势,由1988~1993年的0.55%增加到2003~2008年的1.88%。而一般劳动对经济增长的贡献率呈现下降趋势,由1988~1993年的34.90%下降到2003~2008年的8.01%。物质资本对经济增长的贡献率相对稳定,占到60%左右。科技进步对经济增长的贡献率在20%左右,且随着实际GDP增长率的变化而变化。
5 结论
本文通过构建科技人才对经济增长的贡献率的测算模型,实证研究我国科技人才对经济增长的贡献率。研究结果显示:科技人才对经济增长的贡献率总体呈现上升趋势;1988~1998年我国科技人才对经济增长的平均贡献率大约在0.59%左右;1998~2008年我国科技人才对经济增长的平均贡献率大约在1.38%左右;1988~2008年我国科技人才对经济增长的平均贡献率大约在0.95%左右;1988~2008年我国物质资本对经济增长的贡献率大约在59.14%左右;1988~2008年我国一般劳动对经济增长的贡献率大约在18.30%左右;1988~2008年我国科技进步对经济增长的贡献率大约在21.62%左右。
[1]张军扩.“七五”期间经济效益的综合分析--各要素对经济增长贡献平侧算[J].经济研究,1991,(4).
[2]德怀特·H·泊金斯.中国经济体制改均翔.管理世界[J],1989,(1).
[3]贺菊煌.我国资产的估算[J].数量经济与技术经济研究,1992,(8).
[4]唐志宏.中国平均利润率的估算[J].经济研究[J],1999,(5).
[5]王小鲁,樊纲等.中国经济增长的可持续性———跨世纪的回顾与展望[M].北京:经济科学出版社,2000.
[6]张军,章元.对中国资本存量K的再估计[J].经济研究,2003,(7).
[7]国家统计局编.中国统计年鉴(1990~2009)[M].北京:中国统计出版社.
[8]国家统计局国民经济核算司编.中国国内生产总值核算历史资料(1952~2004)[M].北京:中国统计出版社,2006.
[9]李子奈编著.计量经济学[M].北京:高等教育出版社,2000,(1).
