数字化近景摄影测量在钢结构试验研究中的应用
2011-03-07孟巧玲李宏阶
刘 黎 孟巧玲 李宏阶
(1.三峡大学土木与建筑学院,湖北宜昌 443002;2.湖北煤炭地质一二五队,湖北宜昌 443002)
钢结构特别是钢桁架结构近年来在桥梁等土木工程的建造中有着广泛的应用,相比于其他类型桥梁,钢桁架结构具有跨度大、承载能力强、构造轻巧简洁的特点[1].钢桁架结构的强度和刚度以及变形规律直接关系到它的应用和安全,因而对钢桁架工作性能的测定进行研究极其重要[2],掌握其变形规律,才能合理预测未来的变形大小,及时采取预防或善后措施,确保建筑物的安全使用.
在结构变形测量中,传统的结构变形测量方法比较复杂,且不能满足量测精度要求.数字摄影在成像质量上的极大提高使数字摄影技术在结构试验变形量测中的应用成为可能[3-4].传统的结构变形测量主要采用位移计、百分表和应变片,一般仅在试件关键点和位置布置,而数字摄影不仅可以记录试验过程和试验场景,还可直接由数字图片信息直接获得结构变形结果,乃至结构变形场发展的全过程,并更加直观地展示了结构破坏过程[5].该技术设备简单,对操作空间要求少,具有灵敏度和精度高、设备简易、光路灵活多变、无损被测量物体、无需对被测量物体表面做特殊处理等许多优点,已在宏观、微观领域中被广泛应用,克服了传统电子量测器件不能量测大变形的限制,且测量点数量可以任意设置,节省试验经费.
1 近景摄影测量的基本原理[6]
1.1 基本原理
数字化摄影测量的主要任务是由二维数字化影像恢复空间点的三维坐标.物方点经过像机镜头摄影成像在像平面上(图1),理想的投影成像模型是光学中的小孔成像模型,其本质就是射影几何中的中心透视投影过程.
在二维测量中,一般常用单站摄影测量,由于测量点共面,取Z=0则共线方程(1)可表示为:
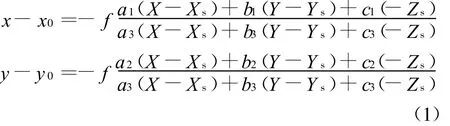
为计算方便,常将ai,bi,ci看成相互独立的参数,则式(1)可表示为

式中,li(i=1~8)为直接线性变换系数
其求解过程一般分为两个步骤:l系数的解算和物方空间坐标(X,Y,Z)的解算.
1.2 各l系数的解算
至少选择4个分布适当的控制点,可以列出多于8个的方程,如式(3)所示,可以采用最小二乘法解得各l系数的值.
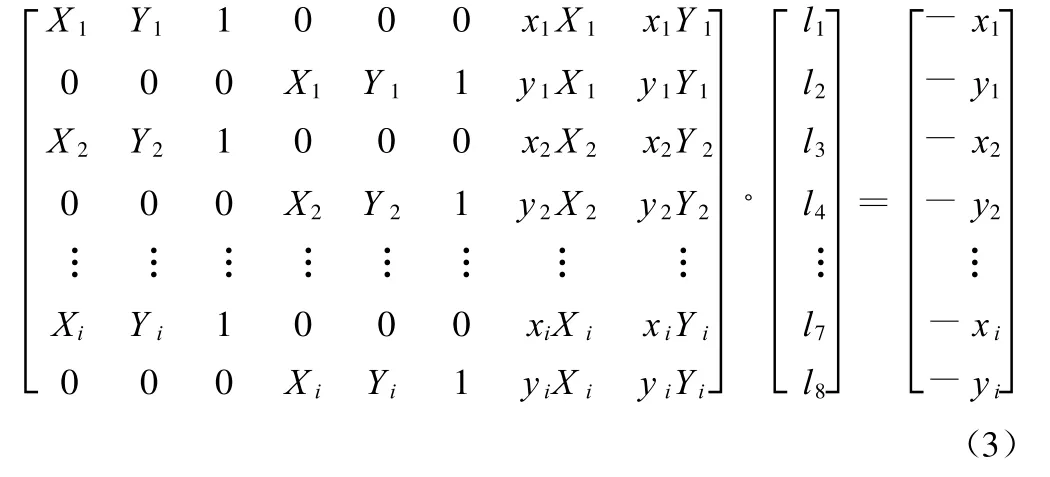
写成矩阵形式为
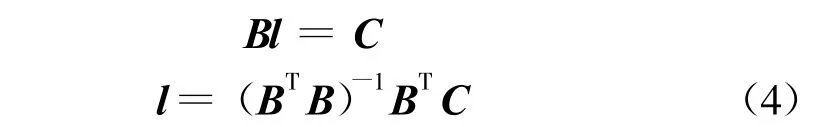
2.3 物方坐标的解算
在求解各个像片的l系数后,对每个物方点,可列出2个的解算物方空间坐标(X,Y)方程如式(5)所示
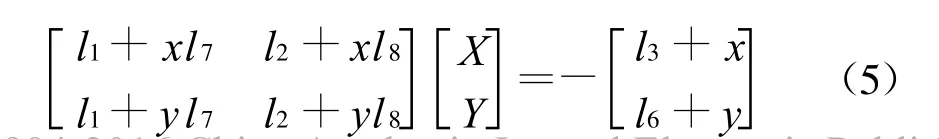
写成矩阵形式为
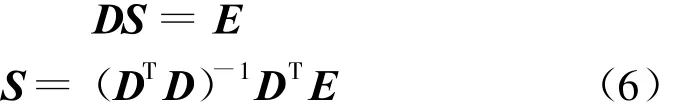
2 目标定位方法[7-8]
由于在该系统中,得到的图会随时间而变化.边缘点选取的合理与否直接关系到测量的精度.标志圆在整个测量过程中可以认为大小不变,因此可以利用这一特性来选取边缘点.
(1)使用Canny法对拍摄的图像进行粗像素提取,可得如图1所示,计算椭圆圆心(m0,n0)与半径(a0,b0),并统计其残差,计算出其标准误差σ0;

图1 粗边缘提取图
(2)根据计算出来的椭圆圆心与半径,对圆进行梯度最大的亚像素边缘提取,并拟合求解出椭圆圆心与半径;
(3)根据求解出的椭圆圆心与半径,再次对圆进行梯度最大的亚像素边缘提取,并拟合求解出椭圆圆心与半径,并采用格拉布斯准则剔除异常数据,拟合求解出椭圆圆心(m,n)与半径(a,b),并统计其残差,计算出其标准误差σ;
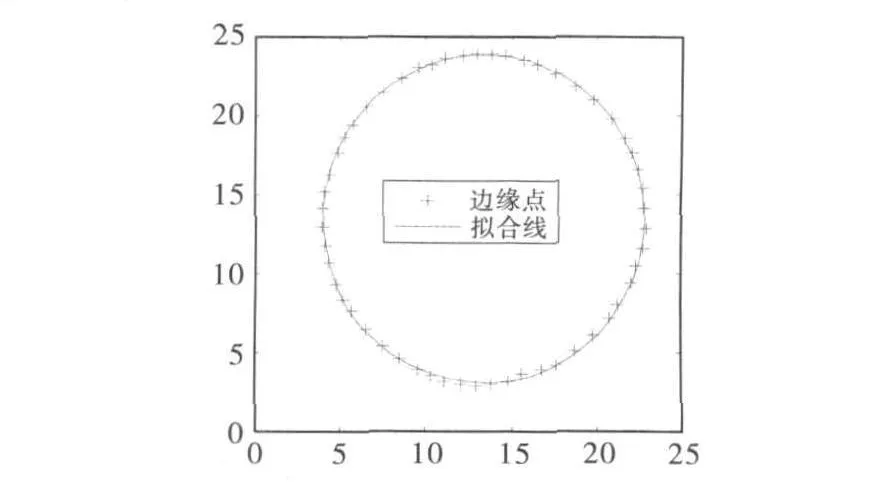
图2 边缘拟合图
(4)当图像是一组连续变化的图像,且变化不是很大,可以采用上一次用到的椭圆圆心坐标作为初始坐标,进行亚像素的边缘提取,然后对提取的边缘使用如下的步骤进行下一步的边缘提取:
对所有的边缘点进行判断,求解目标函数对应的所有边缘点:
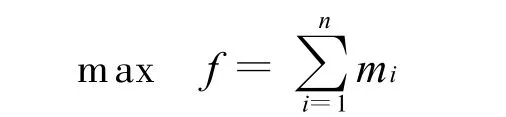
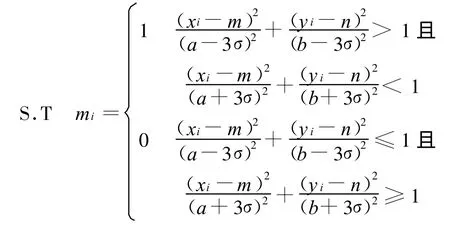
对求取得到最优时的所有边缘点进行拟合求解出椭圆圆心坐标,再进行亚像素边缘提取,利用上面的目标函数进行边缘点的初步剔除,然后利用3σ法则进行边缘剔除,并拟合求解出椭圆圆心.
3 实验及结果分析
3.1 精度测试试验
为了测试该测量系统的精度,采用图3所示的装置进行验证试验.装置包括一个可移动的带有标记点的小型块体,沿着移动方向设有百分表,用以测量块体的位移.测量系统从块体的侧面拍摄图像,并处理得到标记点的位移.表1是两种测量方法得到的试验结果对比表,其中摄像测量数据取百分表相同有效位数.
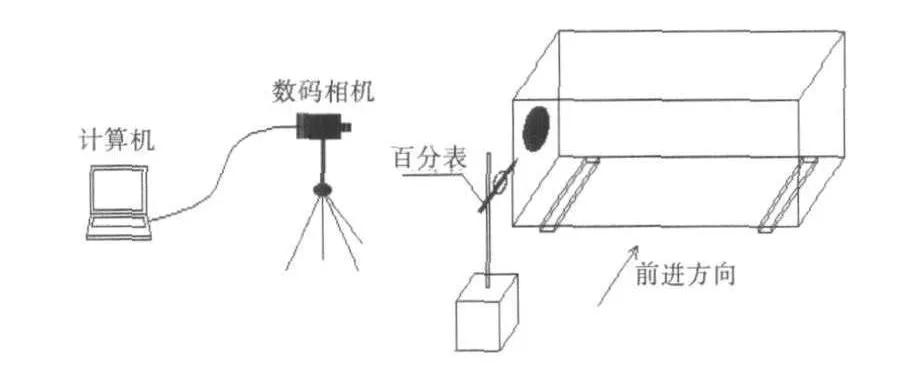
图3 精度测试装置示意图

表1 对比测试结果对照表 (单位:mm)
如果以百分表数据为精确值,根据测量结果,在15.91mm的测量距离内,测量的最大误差为0.07 mm,标准差为0.026 mm,误差百分比为0.16%,可以满足试验的位移测量精度要求.
3.2 试验概况
为了验证钢桁架结构在静荷载作用下的工作性能特性,进行平面应力加载条件下静载模型试验.并采用数码像机数字化近景摄影测量方法来量测桁架各控制点的位移.在杆中间布置了9个应变片(P1~P9),在结点处布置了9个圆形标志点(B1~B9),并在钢桁架重要部位布置了4个百分表测点(K1~K4)用以验证测量精度,如图4所示.其中桁架跨长3.8 m,上下弦采用等边角钢2∠45×4,腹杆采用等边角钢2∠30×4,弹性模量E=2.1×105MPa,自重62.3 kg.
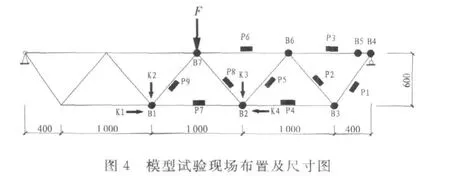

3.3 试验过程
试验按如图6所示过程进行加载.

图6 加载方式
3.4 分析步骤
数字化近景摄影测量进行结构变形测量的全过程简述如下[9]:(1)进行现场摄影,把初始状态及每步加载后的状态用数码像机拍摄下来并存入计算机上; (2)对每张相片中各测点进行坐标量测;(3)对相同加载状态下所拍摄的相片进行各相片间的相对定向,形成各独立相对的独立模型;(4)通过对各独立模型的变换进行模型连接,建立统一的整体模型;(5)通过空间相似变换和绝对定向,实现实际坐标的计算,并将初始状态及各步加载状态下的坐标系统一到同一坐标系中;(6)将每步加载状态下各测点的坐标值与初始状态下相应测点的坐标值相减,即得到不同加载状态下各测点的绝对位移值.数据分析流程如图7所示.

图7 数据分析流程
3.5 试验结果
通过对各级荷载作用下的应变片及百分表进行数据采集,得到如表2~3所示结果.

表2 各应变片应变结果表

表3 各百分表位移结果表
通过对近景摄影测量的图片进行处理,得到各测量点的水平向和竖直向位移值,见表4~5.

表4 各标志点水平位移结果表
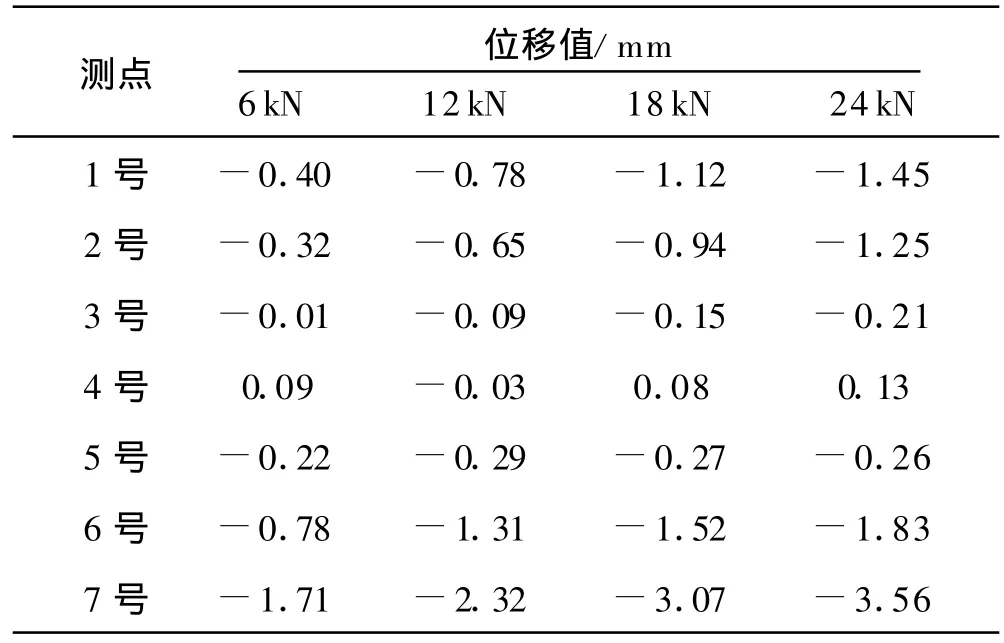
表5 各标志点竖直位移结果表
3.6 结果误差分析
通过各应变片的测量结果表明,除8号的结果异常外,其它数据与理论相符,在实际试验中由于结构的各部分受力与理论不一样,造成在6kN这级荷载作用下,所测量的数据与理论存在一定的偏差.
通过理论计算,每6 kN荷载作用下B1点或B2点的竖直向位移理论计算值为0.36mm,则与数字近景摄影测量中竖直向位移表中对应点的位移(0.35 mm和0.31mm)向接近,由于本次试验的桁架中,各杆是焊接的,与理论计算中的铰接有所不同,故实际测量结果应小于理论计算结果.4号标志点和5号标志点的结果也表明,在开始6 kN的荷载作用下发生了一定的竖向位移,之后基本不变,这与实际试验过程中,开始时桁架与基座未充分接触产生加大的变形,再其后基本不变这一现象相符.7号点为加载点,该点的测量结果也表明了这一规律.
将百分表的测量结果与对应摄影测量结果相比较,如图8所示,结果表明:两者在绝对位移值上存在一定的偏差,但偏差值为线性递增,通过分析,在百分表测量方向与摄影测量坐标系一致时,两者误差较小,而当两者方向不重合时,其值在理论上为线性线性关系,将其线性拟合后,各点线性偏差标准值为: 0.0075mm、0.0088mm、0.0095mm和0.0145mm,相对误差百分比为0.73%、0.55%、0.56%和1.51%.

图8 百分表测量结果与摄影测量结果对比图
4 结 论
本文利用数字近景摄影测量方法对钢桁架结构的工作性能进行了变形监测.并验证了其精度,与传统的变形测量方法相比较,达到了满意的结果.通过试验,得出以下几点结论:
(1)非量测相机数字化近景摄影测量是一种非接触、无损、可测较大范围的全场位移、摄影相片记录的信息可永久保存、随时提取、设备简单、对环境条件要求低、精度较高的位移量测技术.近景摄影测量技术可应用于变形监测中.
(2)数字化近景摄影测量应用静载作用下钢桁架的模型试验中,所测位移规律性好,与试验过程中现象符合很好,与对应点理论值相差较小,与传统的测量方法相比,当两者测试角度偏差较小时,相对误差为0.16%,在本钢桁架测试试验中,相对误差小于1.51%,所得结果准确可靠,在结构变形测量方面有很好的利用价值.
[1] 李 杰,万 鹏,李 娜.钢桁架结构次应力问题的探讨[J].钢结构,2005,20(2):18-20.
[2] 宗听聪.钢结构[M].北京:中国建筑工业出版社,1991.
[3] 朱援祥.数码相机在焊接结构收缩变形测量中的应用[J].焊接,2003,05.
[4] 洪宝宁,赵维炳.利用图象序列测量土工模型位移场的数学模型[J].土木工程学报,1999,32(3):61-65.
[5] 刘雯雯.数字全息技术及其在结构变形测量中的应用研究[D].南京:南京理工大学,2005.
[6] 冯文灏.近景摄影测量[M].武汉:武汉大学出版社, 2002.
[7] 范生宏,黄桂平.Canny算子对人工标志中心的亚像素精度定位[J].测绘科学技术学报,2006,23(1):76-78.
[8] 陈宇云.灰度图像的边缘检测研究[D].成都:电子科技大学,2009.
[9] 任伟中,寇新建.数字化近景摄影测量在模型试验变形测量中的应用[J].岩石力学与工程学报,2004,23(3): 436-440.
