FRP筋混凝土双向板的非线性分析程序设计
2011-03-07朱海堂张东华王宝庭王怡中
朱海堂 张东华 王宝庭 王怡中
(郑州大学水利与环境学院,郑州 450001)
钢筋混凝土双向板广泛应用于港口码头等工程结构中,但由于钢筋耐腐蚀性能差,当混凝土出现裂缝时,钢筋极易发生锈蚀,严重影响结构的安全与耐久性能,甚至发生安全事故.由于FRP筋具有质量轻、强度高、耐腐蚀等优良性能,FRP筋应用于处于恶劣环境下混凝土双向板中将可以有效解决钢筋的锈蚀问题.目前,有限元数值方法在钢筋混凝土结构受力分析中已得到相当广泛的应用[1-6],但对FRP筋增强混凝土结构的数值模拟还较少[7-8].如果可以准确模拟FRP筋混凝土结构的力学行为,那么将为FRP筋混凝土工程结构的设计提供分析依据,以保证工程设计的可靠性.同时,由于国内外对FRP筋增强混凝土双向板结构的研究较少[9-10],正确合理的数值模拟对FRP筋混凝土结构设计理论的完善必将有着积极的现实意义.
1 混凝土材料的本构关系
由于混凝土的性能具有非线性,故本文采用非线性弹性理论中的全量E-ν型混凝土本构关系进行模拟.此模型由Ottosen提出,该本构模型需要明确3个条件:破坏准则、非线性指标及等效应力-应变关系表达式.
(1)破坏准则
本文采用的混凝土破坏准则是由江见鲸改进后的4参数公式:
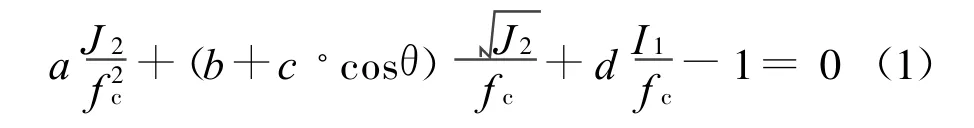
式中,a、b、c和d为待确定的4个参数,I1为应力状态的第一不变量,J2为应力偏量的第二不变量,fc为混凝土轴心抗压强度.
(2)非线性指标
非线性指标是描述实际应力状态与破坏时应力状态相互关系的一个定量指标,该指标表明了应力状态的相对水平,据此确定混凝土变形的非线性程度.
在单向应力状态下,非线性指标定义为

式中,fc是混凝土轴心抗压强度.
非线性指标0≤β≤1,当β=0时,处于未加载状态,β=1时处于破坏状态.通过β的大小我们可以确定混凝土非线性变形程度.

式中,J2f为达到破坏状态时的应力偏量第二不变量.
(3)等效应力-应变关系表达式
混凝土等效应力-应变关系表达式采用Sargin于1971年提出的表达式,即
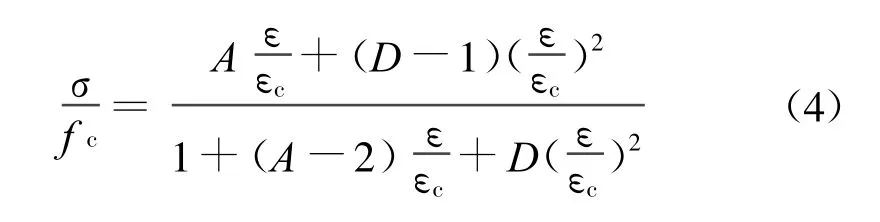
式中,fc是混凝土轴心抗压强度;A=E0/Ec,E0为混凝土初始弹性模量,Ec为混凝土应力达到 fc时的割线模量;εc为应力达到峰值时的应变;D为系数,取值范围0≤D≤1.D值对应力-应变曲线的上升段影响不大,但对下降段有很大影响,D越大,曲线的下降段愈平缓.此曲线基本可以反映混凝土本构关系全曲线的主要特征,在有限元分析中应用广泛.
2 裂缝模型
在有限元分析中主要有两种裂缝模型:分离裂缝模型和弥散裂缝模型.分离裂缝模型是将裂缝表面分离,引入裂缝界面单元后定义裂缝面上的裂缝张开位移和应力间的关系对裂缝的开展进行模拟,因此,在计算过程中需要事先确定开裂面的位置,分析结果中具有一定的人为因素.而弥散裂缝模型不需要预先知道开裂面的位置,而且由于该模型假定混凝土开裂之后材料是连续的,并通过材料的模量和应力的降低来模拟裂缝的开展,从而可以省去大量的重新划分网格单元的工作.本文采用弥散裂缝模型模拟裂缝的开展.
判断裂缝的开裂和发展采用最大拉应力理论(又称第一强度理论):

式中,σt为混凝土中的拉应力;ft为混凝土的轴心抗拉强度,当σt≤ft时混凝土未开裂,当σt>ft时混凝土将在垂直于拉应力的方向上发生开裂.混凝土开裂之后,认为开裂面上的混凝土将不能继续承受拉应力.
3 有限元模型
在本文的有限元分析中,采用三维20节点等参网格单元,有限元模型采用整体式模型,即把FRP筋分布到混凝土单元中.该模型将单元视为连续均匀材料,综合了混凝土和FRP筋单元的刚度矩阵:

式中,[Dc]为混凝土的本构关系矩阵;[Df]为FRP筋的本构关系矩阵;[K]为单元刚度矩阵;B、BT分别是几何矩阵和几何矩阵的转置矩阵.
4 程序设计
本文采用FORT RAN语言编制出非线性有限元程序进行FRP筋混凝土双向板在集中荷载作用下的冲切性能的分析.具体流程如图1所示,其中:INPUT:输入几何条件和材料特性;GRID:网格剖分; BOUNDRY:边界条件;STIFFNESS MATRIX:总刚度矩阵;ELEMENT STIFFNESS:单元刚度矩阵; LOAD3D:根据承受的荷载计算得到的结点荷载向量(荷载包括集中力、重力或均布力);SOLVE EQUATIONS:解方程求结点位移;JUDGE CONVERGENCY:判断是否收敛;JUDGE DIVERGENCY:判断是否发散;CALCULAT E STRESS:计算单元应力状态;MODIFY STIFFNESS MATRIX:重新计算单元刚度矩阵;CONCRETE CRACK:混凝土开裂对刚度矩阵的影响;FRP REBAR:FRP筋的应力状态;CONCRET E NONLINEARITY:混凝土非线性特性;OUTPUT RESULT:输出结果;FINAL LOAD:判断是否为最终荷载;STOP:终止计算.

图1 FRP筋混凝土双向板冲切性能分析程序设计流程图
5 算 例
5.1 试验简介
集中荷载作用下的四边简支FRP筋混凝土双向板,几何尺寸为1800mm×1 800mm×150mm,计算跨度1500mm.实测混凝土强度等级40.5MPa,根据本文1(3)节所述的等效应力-应变关系表达式,取等效应力-应变关系中的参数A=1.5、D=0.5时,混凝土抗拉强度为2.876 MPa;FRP筋配筋率ρ= 0.55%,混凝土保护层厚度为20 mm,试验实测得到的FRP筋拉伸弹性模量为43.648GPa;试验采用板中心集中荷载加载方式,加载面积为150 mm×150 mm,实测双向板开裂荷载为19.6 kN,破坏荷载为245.3kN.
5.2 网格划分
有限元分析时的网格划分如图2所示,X方向划分为12等份,Y方向划分为12等份,Z方向划分为3等份;荷载增量为:20×2kN+50×4 kN+40×1 kN.中置集中荷载作用下的双向板为双向对称构件,因此,在分析中为节省计算时间只分析了原构件1/4部分.对称面位置采用对称面的法向约束来模拟原约束情况.

图2 FRP筋混凝土双向板网格剖分
5.3 有限元计算结果及其与试验结果的对比
根据前述程序设计方法编制了有限元数值分析程序,并对试验板进行了数值模拟计算.计算结果表明:
(1)有限元分析计算得到FRP筋混凝土双向板的开裂荷载是24 kN,较开裂荷载试验值19.6kN略大,为开裂荷载试验值的122.4%;发生开裂的单元编号是133、134及135,通过与网格剖分情况的比较分析可以确定,这几个单元的位置正是板下底面的跨中位置附近,开裂位置与试验结果较为吻合.
(2)有限元分析计算得到FRP筋混凝土双向板的极限荷载为230 kN,较该板的极限荷载试验值245.3kN略小,为试验极限荷载的93.9%,表明该程序可以较好地模拟和分析FRP筋混凝土双向板的极限破坏荷载.
6 结 论
(1)采用弥散裂缝模型可以良好地模拟FRP筋混凝土双向板的开裂过程.
(2)引入非线性指标可以更好地反映出混凝土非线性对构件极限承载力计算结果所造成的影响.
(3)通过有限元分析计算发现,FRP筋混凝土双向板的开裂位置与极限荷载的有限元分析计算结果与试验结果较为吻合,可以利用该程序进行FRP筋混凝土双向板开裂过程模拟和冲切承载能力的计算分析.参考文献:
[1] Rabczuk T,Akkermann J,Eibl J.A Numerical Model forReinforced Concrete Structures[J].Solids and Structures,2005.
[2] 姜庆远,叶燕春,刘宗仁.弥散裂缝模型的应用讨论[J].土木工程学报,2008,41(2):81-85.
[3] Tae-Hyung Lee,Khalid M.Mosalam.Probabilistic Fiber Element Modeling of Reinforced Concrete Structures [J].Computers&Structures,2004,82(27):2285-2299.
[4] 万 宇,艾合买提.依布拉音.混凝土裂缝模型的数值计算及模拟[J].山西建筑,2007,33(34):68-69.
[5] 江见鲸.钢筋混凝土结构非线性有限元分析[M].西安:陕西科学技术出版社,1994.
[6] 方自虎.钢筋混凝土结构的三维有限元程序设计[J].武汉大学学报,2006,39(3):76-80.
[7] Guido Camata,Enrico Spacone,Roko Zarnic.Experimental and Nonlinear Finite Element Studies of RC Beams Strengthened with FRP Plates[J].Composites Part B:Engineering,2007,38(2):277-288.
[8] 周英武.FRP-高强混凝土梁强度与延性的理论与试验研究[D].大连:大连理工大学,2009.
[9] Carlos E.Ospina,Scott D.B.Alexander,J.J.Roger Cheng.Punching of Two-Way Concrete Slabs with Fiber-Reinforced Polymer Reinforcing Bars or Grids[J]. ACI Structural Journal,2003,100(5):589-598.
[10]肖志龙.中置集中荷载作用下FRP筋混凝土双向板冲切性能研究[D].郑州:郑州大学,2010.
